The MI Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Descriptive Statistics EM Algorithm for Data with Missing Values Statistical Assumptions for Multiple Imputation Missing Data Patterns Imputation Methods Monotone Methods for Data Sets with Monotone Missing Patterns Monotone and FCS Regression Methods Monotone and FCS Predictive Mean Matching Methods Monotone Propensity Score Method Monotone and FCS Discriminant Function Methods Monotone and FCS Logistic Regression Methods FCS Methods for Data Sets with Arbitrary Missing Patterns Checking Convergence in FCS Methods MCMC Method for Arbitrary Missing Multivariate Normal Data Producing Monotone Missingness with the MCMC Method MCMC Method Specifications Checking Convergence in MCMC Input Data Sets Output Data Sets Combining Inferences from Multiply Imputed Data Sets Multiple Imputation Efficiency Imputer’s Model Versus Analyst’s Model Parameter Simulation versus Multiple Imputation Summary of Issues in Multiple Imputation ODS Table Names ODS Graphics
Descriptive Statistics EM Algorithm for Data with Missing Values Statistical Assumptions for Multiple Imputation Missing Data Patterns Imputation Methods Monotone Methods for Data Sets with Monotone Missing Patterns Monotone and FCS Regression Methods Monotone and FCS Predictive Mean Matching Methods Monotone Propensity Score Method Monotone and FCS Discriminant Function Methods Monotone and FCS Logistic Regression Methods FCS Methods for Data Sets with Arbitrary Missing Patterns Checking Convergence in FCS Methods MCMC Method for Arbitrary Missing Multivariate Normal Data Producing Monotone Missingness with the MCMC Method MCMC Method Specifications Checking Convergence in MCMC Input Data Sets Output Data Sets Combining Inferences from Multiply Imputed Data Sets Multiple Imputation Efficiency Imputer’s Model Versus Analyst’s Model Parameter Simulation versus Multiple Imputation Summary of Issues in Multiple Imputation ODS Table Names ODS Graphics -
Examples
 EM Algorithm for MLE Monotone Propensity Score Method Monotone Regression Method Monotone Logistic Regression Method for CLASS Variables Monotone Discriminant Function Method for CLASS Variables FCS Method for Continuous Variables FCS Method for CLASS Variables FCS Method with Trace Plot MCMC Method Producing Monotone Missingness with MCMC Checking Convergence in MCMC Saving and Using Parameters for MCMC Transforming to Normality Multistage Imputation
EM Algorithm for MLE Monotone Propensity Score Method Monotone Regression Method Monotone Logistic Regression Method for CLASS Variables Monotone Discriminant Function Method for CLASS Variables FCS Method for Continuous Variables FCS Method for CLASS Variables FCS Method with Trace Plot MCMC Method Producing Monotone Missingness with MCMC Checking Convergence in MCMC Saving and Using Parameters for MCMC Transforming to Normality Multistage Imputation - References
| FCS Statement (Experimental) |
The FCS statement specifies a multivariate imputation by fully conditional specification methods. If you specify an FCS statement, you must also specify a VAR statement.
Table 56.2 summarizes the options available for the FCS statement.
Option |
Description |
|---|---|
Imputation Details |
|
Specifies the number of burn-in iterations |
|
Specifies the variable ordering in the filled-in and imputation phases |
|
Data Set |
|
Outputs parameter estimates used in iterations |
|
ODS Output Graphics |
|
Displays trace plots |
|
Imputation Methods |
|
Specifies the discriminant function method |
|
Specifies the logistic regression method |
|
Specifies the regression method |
|
Specifies the predictive mean matching method |
|
The following options are available for the FCS statement in addition to the imputation methods specified (in alphabetical order):
- NBITER=number
specifies the number of burn-in iterations before each imputation. The default is NBITER=10.
- ORDER=FREQ | VAR
specifies the variable ordering in which to impute missing values in the filled-in and imputation phases. The ORDER=FREQ option orders the variables by the descending frequency counts of variables and the ORDER=VAR orders the variables as specified in the VAR statement. The default is ORDER=FREQ.
- OUTITER <( options )> =SAS-data-set
-
creates an output SAS data set of TYPE=COV that contains parameters used in the imputation step for each iteration. The data set includes variables named _Imputation_ and _Iteration_ to identify the imputation number and iteration number.
The parameters in the output data set depend on the options specified. You can specify the options MEAN and STD to output parameters of means and standard deviations, respectively. When no options are specified, the output data set contains the mean parameters used in the imputation step for each iteration. See the section Output Data Sets for a description of this data set.
- PLOTS <( LOG )> <= TRACE < ( trace-options ) >>
-
requests statistical graphics of trace plots from iterations via the Output Delivery System (ODS).
ODS Graphics must be enabled before requesting plots. For example:
ods graphics on; proc mi data=Fitness1 seed=501213 mu0=50 10 180; mcmc plots=(trace(mean(Oxygen)) acf(mean(Oxygen))); var Oxygen RunTime RunPulse; run; ods graphics off;
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21, Statistical Graphics Using ODS.
The global plot option LOG requests that the logarithmic transformations of parameters be used. The default is PLOTS=TRACE(MEAN).
The available trace-options are as follows:
- MEAN < ( variables ) >
displays plots of means for continuous variables in the list. When the MEAN option is specified without variables, all continuous variables are used.
- STD < ( variables ) >
displays plots of standard deviations for continuous variables in the list. When the STD option is specified without variables, all continuous variables are used.
The discriminant function, logistic regression, regression, and predictive mean matching methods are available in the FCS statement. You specify each method with the syntax
method < ( <imputed < = effects > > </ options> ) >
That is, for each method, you can specify the imputed variables and, optionally, a set of effects to impute these variables. Each effect is a variable or a combination of variables in the VAR statement. The syntax for the specification of effects is the same as for the GLM procedure. See Chapter 41, The GLM Procedure, for more information.
One general form of an effect involving several variables is
X1  X2
X2  A
A  B
B  C
C 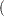 D E
D E 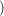
where A, B, C, D, and E are classification variables and X1 and X2 are continuous variables.
When an FCS statement is used without specifying any methods, the regression method is used for all continuous variables and the discriminant function method is used for all classification variables. For each imputed variable, all other variables in the VAR statement are used as the covariates.
When a method for continuous variables is specified without imputed variables, the method is used for all continuous variables in the VAR statement that are not specified in other methods. Similarly, when a method for classification variables is specified without imputed variables, the method is used for all classification variables in the VAR statement that are not specified in other methods.
For each imputed variable, if no covariates are specified, then all other variables in the VAR statement are used as the covariates. That is, each continuous variable is used as a regressor effect, and each classification variable is used as a main effect. For the discriminant function method, only the continuous variables can be used as covariate effects.
With an FCS statement, the variables are imputed sequentially in the order specified in the ORDER= option. For a continuous variable, you can use a regression method or a regression predicted mean matching method to impute missing values. For a nominal classification variable, you can use a discriminant function method to impute missing values without using the ordering of the class levels. For an ordinal classification variable, you can use a logistic regression method to impute missing values by using the ordering of the class levels. For a binary classification variable, either a discriminant function method or a logistic regression method can be used. By default, a regression method is used for a continuous variable, and a discriminant function method is used for a classification variable.
Note that except for the regression method, all other methods impute values from the observed values. See the section FCS Methods for Data Sets with Arbitrary Missing Patterns for a detailed description of the FCS methods.
You can specify the following imputation methods in an FCS statement (in alphabetical order):
-
DISCRIM <( imputed < = effects> <
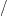 options> ) >
options> ) >
-
specifies the discriminant function method of classification variables. Only the continuous variables are allowed as covariate effects. The available options are DETAILS, PCOV=, and PRIOR=. The DETAILS option displays the group means and pooled covariance matrix used in each imputation. The PCOV= option specifies the pooled covariance used in the discriminant method. Valid values for the PCOV= option are as follows:
- FIXED
uses the observed-data pooled covariance matrix for each imputation.
- POSTERIOR
draws a pooled covariance matrix from its posterior distribution.
The default is PCOV=POSTERIOR. See the section Monotone and FCS Discriminant Function Methods for a detailed description of the method.
The PRIOR= option specifies the prior probabilities of group membership. Valid values for the PRIOR= option are as follows:
- EQUAL
sets the prior probabilities equal for all groups.
- PROPORTIONAL
sets the prior probabilities proportion to the group sample sizes.
- JEFFREYS < =c >
specifies a noninformative prior,
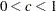 . If the number
. If the number  is not specified, JEFFREYS=0.5.
is not specified, JEFFREYS=0.5. - RIDGE < =d >
specifies a ridge prior,
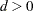 . If the number
. If the number 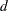 is not specified, RIDGE=0.25.
is not specified, RIDGE=0.25.
The default is PRIOR=JEFFREYS. See the section Monotone and FCS Discriminant Function Methods for a detailed description of the method.
-
LOGISTIC <( imputed < = effects> <
 options> ) >
options> ) >
-
specifies the logistic regression method of classification variables. The available options are DETAILS, ORDER=, and DESCENDING. The DETAILS option displays the regression coefficients in the logistic regression model used in each imputation.
When the imputed variable has more than two response levels, the ordinal logistic regression method is used. The ORDER= option specifies the sorting order for the levels of the response variable. Valid values for the ORDER= option are as follows:
- DATA
sorts by the order of appearance in the input data set.
- FORMATTED
sorts by their external formatted values.
- FREQ
sorts by the descending frequency counts.
- INTERNAL
sorts by the unformatted values.
By default, ORDER=FORMATTED.
The option DESCENDING reverses the sorting order for the levels of the response variables.
See the section Monotone and FCS Logistic Regression Methods for a detailed description of the method.
-
REG | REGRESSION <( imputed < = effects> <
 DETAILS> ) >
DETAILS> ) >
-
specifies the regression method of continuous variables. The DETAILS option displays the regression coefficients in the regression model used in each imputation.
With a regression method, the MAXIMUM=, MINIMUM=, and ROUND= options can be used to make the imputed values more consistent with the observed variable values.
See the section Monotone and FCS Regression Methods for a detailed description of the method.
- REGPMM < ( imputed < = effects> < options> ) >
- REGPREDMEANMATCH < ( imputed < = effects > < options > ) >
-
specifies the predictive mean matching method for continuous variables. This method is similar to the regression method except that it imputes a value randomly from a set of observed values whose predicted values are closest to the predicted value for the missing value from the simulated regression model (Heitjan and Little 1991; Schenker and Taylor 1996).
The available options are DETAILS and K=. The DETAILS option displays the regression coefficients in the regression model used in each imputation. The K= option specifies the number of closest observations to be used in the selection. The default is K=5.
See the section Monotone and FCS Predictive Mean Matching Methods for a detailed description of the method.
With an FCS statement, the missing values of variables in the VAR statement are imputed. After the initial filled in, these variables with missing values are imputed sequentially in the order specified in the VAR statement. For example, the following MI procedure statements use the regression method to impute variable 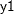 from effect
from effect 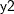 , the regression method to impute variable
, the regression method to impute variable 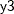 from effects
from effects 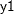 and
and 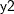 , the logistic regression method to impute variable
, the logistic regression method to impute variable 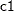 from effects
from effects 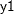 ,
, 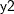 , and
, and 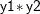 , and the default regression method for continuous variables to impute variable
, and the default regression method for continuous variables to impute variable 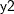 from effects
from effects 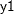 ,
, 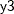 , and
, and 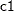 :
:
proc mi; class c1; fcs reg(y1= y2) reg(y3= y1 y2) logistic(c1= y1 y2 y1*y2); var y1 y2 y3 c1; run;