The MI Procedure
- Overview
- Getting Started
-
Syntax
-
Details
Descriptive Statistics EM Algorithm for Data with Missing Values Statistical Assumptions for Multiple Imputation Missing Data Patterns Imputation Methods Monotone Methods for Data Sets with Monotone Missing Patterns Monotone and FCS Regression Methods Monotone and FCS Predictive Mean Matching Methods Monotone Propensity Score Method Monotone and FCS Discriminant Function Methods Monotone and FCS Logistic Regression Methods FCS Methods for Data Sets with Arbitrary Missing Patterns Checking Convergence in FCS Methods MCMC Method for Arbitrary Missing Multivariate Normal Data Producing Monotone Missingness with the MCMC Method MCMC Method Specifications Checking Convergence in MCMC Input Data Sets Output Data Sets Combining Inferences from Multiply Imputed Data Sets Multiple Imputation Efficiency Imputer’s Model Versus Analyst’s Model Parameter Simulation versus Multiple Imputation Summary of Issues in Multiple Imputation ODS Table Names ODS Graphics
-
Examples
EM Algorithm for MLE Monotone Propensity Score Method Monotone Regression Method Monotone Logistic Regression Method for CLASS Variables Monotone Discriminant Function Method for CLASS Variables FCS Method for Continuous Variables FCS Method for CLASS Variables FCS Method with Trace Plot MCMC Method Producing Monotone Missingness with MCMC Checking Convergence in MCMC Saving and Using Parameters for MCMC Transforming to Normality Multistage Imputation
- References
| Descriptive Statistics |
Suppose 
is the 
matrix of complete data, which might not be fully observed, 
is the number of observations fully observed, and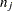 
is the number of observations with observed values for variable 
.
With complete cases, the sample mean vector is
 |
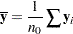and the CSSCP matrix is
 |
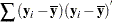where each summation is over the fully observed observations.
The sample covariance matrix is
 |
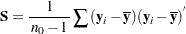and is an unbiased estimate of the covariance matrix.
The correlation matrix 
, which contains the Pearson product-moment correlations of the variables, is derived by scaling the corresponding covariance matrix:
 |
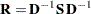where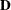 
is a diagonal matrix whose diagonal elements are the square roots of the diagonal elements of 
.
With available cases, the corrected sum of squares for variable is
 |
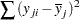where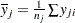 
is the sample mean and each summation is over observations with observed values for variable .
The variance is
 |
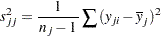The correlations for available cases contain pairwise correlations for each pair of variables. Each correlation is computed from all observations that have nonmissing values for the corresponding pair of variables.