The LIFEREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing Values Model Specification Computational Method Supported Distributions Predicted Values Confidence Intervals Fit Statistics Probability Plotting INEST= Data Set OUTEST= Data Set XDATA= Data Set Computational Resources Bayesian Analysis Displayed Output for Classical Analysis Displayed Output for Bayesian Analysis ODS Table Names ODS Graphics
Missing Values Model Specification Computational Method Supported Distributions Predicted Values Confidence Intervals Fit Statistics Probability Plotting INEST= Data Set OUTEST= Data Set XDATA= Data Set Computational Resources Bayesian Analysis Displayed Output for Classical Analysis Displayed Output for Bayesian Analysis ODS Table Names ODS Graphics -
Examples
 Motorette Failure Computing Predicted Values for a Tobit Model Overcoming Convergence Problems by Specifying Initial Values Analysis of Arbitrarily Censored Data with Interaction Effects Probability Plotting—Right Censoring Probability Plotting—Arbitrary Censoring Bayesian Analysis of Clinical Trial Data
Motorette Failure Computing Predicted Values for a Tobit Model Overcoming Convergence Problems by Specifying Initial Values Analysis of Arbitrarily Censored Data with Interaction Effects Probability Plotting—Right Censoring Probability Plotting—Arbitrary Censoring Bayesian Analysis of Clinical Trial Data - References
Example 50.2 Computing Predicted Values for a Tobit Model
The LIFEREG procedure can be used to perform a Tobit analysis. The Tobit model, described by Tobin (1958), is a regression model for left-censored data assuming a normally distributed error term. The model parameters are estimated by maximum likelihood. PROC LIFEREG provides estimates of the parameters of the distribution of the uncensored data. See Greene (1993) and Maddala (1983) for a more complete discussion of censored normal data and related distributions. This example shows how you can use PROC LIFEREG and the DATA step to compute two of the three types of predicted values discussed there.
Consider a continuous random variable Y and a constant C. If you were to sample from the distribution of Y but discard values less than (greater than) C, the distribution of the remaining observations would be truncated on the left (right). If you were to sample from the distribution of Y and report values less than (greater than) C as C, the distribution of the sample would be left (right) censored.
The probability density function of the truncated random variable 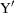 is given by
is given by
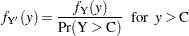 |
where 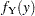 is the probability density function of Y. PROC LIFEREG cannot compute the proper likelihood function to estimate parameters or predicted values for a truncated distribution. Suppose the model being fit is specified as follows:
is the probability density function of Y. PROC LIFEREG cannot compute the proper likelihood function to estimate parameters or predicted values for a truncated distribution. Suppose the model being fit is specified as follows:
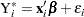 |
where 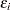 is a normal error term with zero mean and standard deviation
is a normal error term with zero mean and standard deviation  .
.
Define the censored random variable 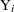 as
as
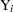 |
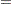 |
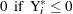 |
|||
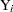 |
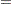 |
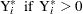 |
This is the Tobit model for left-censored normal data. 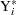 is sometimes called the latent variable. PROC LIFEREG estimates parameters of the distribution of
is sometimes called the latent variable. PROC LIFEREG estimates parameters of the distribution of 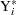 by maximum likelihood.
by maximum likelihood.
You can use the LIFEREG procedure to compute predicted values based on the mean functions of the latent and observed variables. The mean of the latent variable 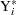 is
is  , and you can compute values of the mean for different settings of
, and you can compute values of the mean for different settings of  by specifying XBETA=variable-name in an OUTPUT statement. Estimates of
by specifying XBETA=variable-name in an OUTPUT statement. Estimates of  for each observation will be written to the OUT= data set. Predicted values of the observed variable
for each observation will be written to the OUT= data set. Predicted values of the observed variable 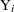 can be computed based on the mean
can be computed based on the mean
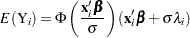 |
where
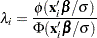 |
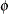 and
and 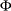 represent the normal probability density and cumulative distribution functions.
represent the normal probability density and cumulative distribution functions.
Although the distribution of 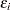 in the Tobit model is often assumed normal, you can use other distributions for the Tobit model in the LIFEREG procedure by specifying a distribution with the DISTRIBUTION= option in the MODEL statement. One distribution that should be mentioned is the logistic distribution. For this distribution, the MLE has bounded influence function with respect to the response variable, but not the design variables. If you believe your data have outliers in the response direction, you might try this distribution for some robust estimation of the Tobit model.
in the Tobit model is often assumed normal, you can use other distributions for the Tobit model in the LIFEREG procedure by specifying a distribution with the DISTRIBUTION= option in the MODEL statement. One distribution that should be mentioned is the logistic distribution. For this distribution, the MLE has bounded influence function with respect to the response variable, but not the design variables. If you believe your data have outliers in the response direction, you might try this distribution for some robust estimation of the Tobit model.
With the logistic distribution, the predicted values of the observed variable 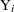 can be computed based on the mean of
can be computed based on the mean of 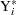 ,
,
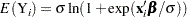 |
The following table shows a subset of the Mroz (1987) data set. In these data, Hours is the number of hours the wife worked outside the household in a given year, Yrs_Ed is the years of education, and Yrs_Exp is the years of work experience. A Tobit model will be fit to the hours worked with years of education and experience as covariates.
Hours |
Yrs_Ed |
Yrs_Exp |
|---|---|---|
0 |
8 |
9 |
0 |
8 |
12 |
0 |
9 |
10 |
0 |
10 |
15 |
0 |
11 |
4 |
0 |
11 |
6 |
1000 |
12 |
1 |
1960 |
12 |
29 |
0 |
13 |
3 |
2100 |
13 |
36 |
3686 |
14 |
11 |
1920 |
14 |
38 |
0 |
15 |
14 |
1728 |
16 |
3 |
1568 |
16 |
19 |
1316 |
17 |
7 |
0 |
17 |
15 |
If the wife was not employed (worked 0 hours), her hours worked will be left censored at zero. In order to accommodate left censoring in PROC LIFEREG, you need two variables to indicate censoring status of observations. You can think of these variables as lower and upper endpoints of interval censoring. If there is no censoring, set both variables to the observed value of Hours. To indicate left censoring, set the lower endpoint to missing and the upper endpoint to the censored value, zero in this case.
The following statements create a SAS data set with the variables Hours, Yrs_Ed, and Yrs_Exp from the preceding data. A new variable, Lower, is created such that Lower=. if Hours=0 and Lower=Hours if Hours>0.
data subset;
input Hours Yrs_Ed Yrs_Exp @@;
if Hours eq 0
then Lower=.;
else Lower=Hours;
datalines;
0 8 9 0 8 12 0 9 10 0 10 15 0 11 4 0 11 6
1000 12 1 1960 12 29 0 13 3 2100 13 36
3686 14 11 1920 14 38 0 15 14 1728 16 3
1568 16 19 1316 17 7 0 17 15
;
run;
The following statements fit a normal regression model to the left-censored Hours data with Yrs_Ed and Yrs_Exp as covariates. You need the estimated standard deviation of the normal distribution to compute the predicted values of the censored distribution from the preceding formulas. The data set OUTEST contains the standard deviation estimate in a variable named _SCALE_. You also need estimates of  . These are contained in the data set OUT as the variable Xbeta.
. These are contained in the data set OUT as the variable Xbeta.
proc lifereg data=subset outest=OUTEST(keep=_scale_); model (lower, hours) = yrs_ed yrs_exp / d=normal; output out=OUT xbeta=Xbeta; run;
Output 50.2.1 shows the results of the model fit. These tables show parameter estimates for the uncensored, or latent variable, distribution.
| Model Information | |
|---|---|
| Data Set | WORK.SUBSET |
| Dependent Variable | Lower |
| Dependent Variable | Hours |
| Number of Observations | 17 |
| Noncensored Values | 8 |
| Right Censored Values | 0 |
| Left Censored Values | 9 |
| Interval Censored Values | 0 |
| Number of Parameters | 4 |
| Name of Distribution | Normal |
| Log Likelihood | -74.9369977 |
| Analysis of Maximum Likelihood Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 95% Confidence Limits | Chi-Square | Pr > ChiSq | |
| Intercept | 1 | -5598.64 | 2850.248 | -11185.0 | -12.2553 | 3.86 | 0.0495 |
| Yrs_Ed | 1 | 373.1477 | 191.8872 | -2.9442 | 749.2397 | 3.78 | 0.0518 |
| Yrs_Exp | 1 | 63.3371 | 38.3632 | -11.8533 | 138.5276 | 2.73 | 0.0987 |
| Scale | 1 | 1582.870 | 442.6732 | 914.9433 | 2738.397 | ||
The following statements combine the two data sets created by PROC LIFEREG to compute predicted values for the censored distribution. The OUTEST= data set contains the estimate of the standard deviation from the uncensored distribution, and the OUT= data set contains estimates of  .
.
data predict;
drop lambda _scale_ _prob_;
set out;
if _n_ eq 1 then set outest;
lambda = pdf('NORMAL',Xbeta/_scale_)
/ cdf('NORMAL',Xbeta/_scale_);
Predict = cdf('NORMAL', Xbeta/_scale_)
* (Xbeta + _scale_*lambda);
label Xbeta='MEAN OF UNCENSORED VARIABLE'
Predict = 'MEAN OF CENSORED VARIABLE';
run;
Output 50.2.2 shows the original variables, the predicted means of the uncensored distribution, and the predicted means of the censored distribution.
| Hours | Lower | Yrs_Ed | Yrs_Exp | MEAN OF UNCENSORED VARIABLE |
MEAN OF CENSORED VARIABLE |
|---|---|---|---|---|---|
| 0 | . | 8 | 9 | -2043.42 | 73.46 |
| 0 | . | 8 | 12 | -1853.41 | 94.23 |
| 0 | . | 9 | 10 | -1606.94 | 128.10 |
| 0 | . | 10 | 15 | -917.10 | 276.04 |
| 0 | . | 11 | 4 | -1240.67 | 195.76 |
| 0 | . | 11 | 6 | -1113.99 | 224.72 |
| 1000 | 1000 | 12 | 1 | -1057.53 | 238.63 |
| 1960 | 1960 | 12 | 29 | 715.91 | 1052.94 |
| 0 | . | 13 | 3 | -557.71 | 391.42 |
| 2100 | 2100 | 13 | 36 | 1532.42 | 1672.50 |
| 3686 | 3686 | 14 | 11 | 322.14 | 805.58 |
| 1920 | 1920 | 14 | 38 | 2032.24 | 2106.81 |
| 0 | . | 15 | 14 | 885.30 | 1170.39 |
| 1728 | 1728 | 16 | 3 | 561.74 | 951.69 |
| 1568 | 1568 | 16 | 19 | 1575.13 | 1708.24 |
| 1316 | 1316 | 17 | 7 | 1188.23 | 1395.61 |
| 0 | . | 17 | 15 | 1694.93 | 1809.97 |