The LIFEREG Procedure
- Overview
-
Getting Started
-
Syntax
-
Details
Missing Values Model Specification Computational Method Supported Distributions Predicted Values Confidence Intervals Fit Statistics Probability Plotting INEST= Data Set OUTEST= Data Set XDATA= Data Set Computational Resources Bayesian Analysis Displayed Output for Classical Analysis Displayed Output for Bayesian Analysis ODS Table Names ODS Graphics
-
Examples
Motorette Failure Computing Predicted Values for a Tobit Model Overcoming Convergence Problems by Specifying Initial Values Analysis of Arbitrarily Censored Data with Interaction Effects Probability Plotting—Right Censoring Probability Plotting—Arbitrary Censoring Bayesian Analysis of Clinical Trial Data
- References
| Fit Statistics |
Suppose that the model contains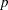 
parameters and that 
observations are used in model fitting. The fit criteria displayed by the LIFEREG procedure are calculated as follows:
-
2 log likelihood: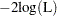 
where L is the maximized likelihood for the model.
-
Akaike’s information criterion:
-
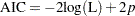
corrected Akaike’s information criterion:
-
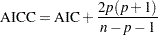
Bayesian information criterion:
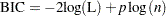
If you specify the Weibull, exponential, lognormal, log-logistic, or gamma distribution, then maximum likelihood estimates of model parameters are computed by maximizing the log likelihood of the distribution of the logarithm of the response. This is equivalent to computing maximum likelihood parameter estimates based on the response on the original, rather than log, scale. If you specify the Weibull, exponential, lognormal, log-logistic, or gamma distribution, then fit statistics based on the maximized log likelihood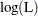 
of the log of the response are reported in the "Fit Statistics" table. Fit criteria computed in this way cannot be meaningfully compared with fit criteria that are based on the log likelihood of the unlogged response. If you specify the normal or logistic distribution, or if you specify the NOLOG option in the MODEL statement, then the fit criteria reported in the "Fit Statistics" table are based on the response on the original, rather than log, scale.
In addition to the "Fit Statistics" table described previously, if you specify the Weibull, exponential, lognormal, log-logistic, or gamma distribution, fit criteria that are based on the distribution of the response on the original scale, rather than the log of the response, are reported in the "Fit Statistics (Unlogged Response)" table.
When comparing models, you should compare fit criteria based on the log likelihood that is computed by using the response on the same scale, either always based on the log of the response or always based on the response on the original scale.
Refer to Akaike (1981, 1979) for details of AIC and BIC. Refer to Simonoff (2003) for a discussion of using AIC, AICC, and BIC in statistical modeling.