The LIFEREG Procedure

MODEL Statement

<label:>

MODEL response<*censor(list)>=effects </ options> ;

<label:>

MODEL (lower,upper)=effects </ options> ;

<label:>

MODEL events/trials=effects </ options> ;

Only a single MODEL statement can be used with one invocation of the LIFEREG procedure. If multiple MODEL statements are present, only the last is used. The optional label is used to label the model estimates in the output SAS data set and OUTEST= data set.

The first MODEL syntax is appropriate for right censoring. The variable response is possibly right censored. If the response variable can be right censored, then a second variable, denoted censor, must appear after the response variable with a list of parenthesized values, separated by commas or blanks, to indicate censoring. That is, if the censor variable takes on a value given in the list, the response is a right-censored value; otherwise, it is an observed value.

The second MODEL syntax specifies two variables, lower and upper, that contain values of the endpoints of the censoring interval. If the two values are the same (and not missing), it is assumed that there is no censoring and the actual response value is observed. If the lower value is missing, then the upper value is used as a left-censored value. If the upper value is missing, then the lower value is taken as a right-censored value. If both values are present and the lower value is less than the upper value, it is assumed that the values specify a censoring interval. If the lower value is greater than the upper value or both values are missing, then the observation is not used in the analysis, although predicted values can still be obtained if none of the covariates are missing. The following table summarizes the ways of specifying censoring.

lower	upper	Comparison	Interpretation
Not missing	Not missing	Equal	No censoring
Not missing	Not missing	Lower < upper	Censoring interval
Missing	Not missing		Upper used as left-
			censoring value
Not missing	Missing		Lower used as right-
			censoring value
Not missing	Not missing	Lower > upper	Observation not used
Missing	Missing		Observation not used

The third MODEL syntax specifies two variables that contain count data for a binary response. The value of the first variable, events, is the number of successes. The value of the second variable, trials, is the number of tries. The values of both events and (trials-events) must be nonnegative, and trials must be positive for the response to be valid. The values of the two variables do not need to be integers and are not modified to be integers.

The effects following the equal sign are the covariates in the model. Higher-order effects, such as interactions and nested terms, are allowed in the list, similar to the GLM procedure. Variable names and combinations of variable names representing higher-order terms are allowed to appear in this list. Classification, or CLASS, variables can be used as effects, and indicator variables are generated for the class levels. If you do not specify any covariates following the equal sign, an intercept-only model is fit.

Examples of three valid MODEL statements follow:

   a: model time*flag(1,3)=temp;
 
   b: model (start, finish)=;
 
   c: model r/n=dose;

MODEL statement a indicates that the response is contained in a variable named time and that, if the variable flag takes on the values 1 or 3, the observation is right censored. The explanatory variable is temp, which could be a CLASS variable. MODEL statement b indicates that the response is known to be in the interval between the values of the variables start and finish and that there are no covariates except for a default intercept term. MODEL statement c indicates a binary response, with the variable r containing the number of responses and the variable n containing the number of trials.

The following options can appear in the MODEL statement.

Task		Option
Model specification
	Sets the significance level	ALPHA=
	Specifies the distribution type for failure time	DISTRIBUTION=
	Requests no log transformation of response	NOLOG
	Initial estimate for intercept term	INTERCEPT=
	Holds the intercept term fixed	NOINT
	Initial estimates for regression parameters	INITIAL=
	Initializes the scale parameter	SCALE=
	Holds the scale parameter fixed	NOSCALE
	Initializes the first shape parameter	SHAPE1=
	Holds the first shape parameter fixed	NOSHAPE1
Model fitting
	Sets the convergence criterion	CONVERGE=
	Sets the maximum number of iterations	MAXITER=
	Sets the tolerance for testing singularity	SINGULAR=
Output
	Displays the estimated correlation matrix	CORRB
	Displays the estimated covariance matrix	COVB
	Displays the iteration history, final gradient,	ITPRINT
	and second derivative matrix

ALPHA=value

sets the significance level for the confidence intervals for regression parameters and estimated survival probabilities. The value must be between 0 and 1. By default, ALPHA=0.05.

CONVERGE=value

sets the convergence criterion. Convergence is declared when the maximum change in the parameter estimates between Newton-Raphson steps is less than the value specified. The change is a relative change if the parameter is greater than 0.01 in absolute value; otherwise, it is an absolute change. By default, CONVERGE=1E $\text{[math]}$ 8.

CONVG=value

sets the relative Hessian convergence criterion; value must be between 0 and 1. After convergence is determined with the change in parameter criterion specified with the CONVERGE= option, the quantity 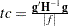$\text{[math]}$ is computed and compared to value, where g is the gradient vector, H is the Hessian matrix for the model parameters, and 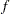$\text{[math]}$ is the log-likelihood function. If 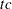$\text{[math]}$ is greater than value, a warning that the relative Hessian convergence criterion has been exceeded is displayed. This criterion detects the occasional case where the change in parameter convergence criterion is satisfied, but a maximum in the log-likelihood function has not been attained. By default, CONVG=1E $\text{[math]}$ 4.

CORRB

produces the estimated correlation matrix of the parameter estimates.

COVB

produces the estimated covariance matrix of the parameter estimates.

DISTRIBUTION=distribution-type

DIST=distribution-type

D=distribution-type

specifies the distribution type assumed for the failure time. By default, PROC LIFEREG fits a type 1 extreme-value distribution to the log of the response. This is equivalent to fitting the Weibull distribution, since the scale parameter for the extreme-value distribution is related to a Weibull shape parameter and the intercept is related to the Weibull scale parameter in this case. When the NOLOG option is specified, PROC LIFEREG models the untransformed response with a type 1 extreme-value distribution as the default. See the section Supported Distributions for descriptions of the distributions. The following are valid values for distribution-type:

EXPONENTIAL: the exponential distribution, which is treated as a restricted Weibull distribution
GAMMA: a generalized gamma distribution (Lawless; 2003, p. 240). The standard two-parameter gamma distribution is not available in PROC LIFEREG.
LLOGISTIC: a log-logistic distribution
LNORMAL: a lognormal distribution
LOGISTIC: a logistic distribution (equivalent to LLOGISTIC when the NOLOG option is specified)
NORMAL: a normal distribution (equivalent to LNORMAL when the NOLOG option is specified)
WEIBULL: a Weibull distribution. If NOLOG is specified, it fits a type 1 extreme-value distribution to the raw, untransformed data.

By default, PROC LIFEREG transforms the response with the natural logarithm before fitting the specified model when you specify the GAMMA, LLOGISTIC, LNORMAL, or WEIBULL option. You can suppress the log transformation with the NOLOG option. The following table summarizes the resulting distributions when the preceding distribution options are used in combination with the NOLOG option.

DISTRIBUTION=	NOLOG Specified?	Resulting Distribution
EXPONENTIAL	No	Exponential
EXPONENTIAL	Yes	One-parameter extreme value
GAMMA	No	Genralized log-gamma using the log of the response.
		(This is the same as fitting the generalized gamma
		using the untransformed response.)
GAMMA	Yes	Generalized log-gamma with untransformed responses
LOGISTIC	No	Logistic
LOGISTIC	Yes	Logistic (NOLOG has no effect)
LLOGISTIC	No	Log-logistic
LLOGISTIC	Yes	Logistic
LNORMAL	No	Lognormal
LNORMAL	Yes	Normal
NORMAL	No	Normal
NORMAL	Yes	Normal (NOLOG has no effect)
WEIBULL	No	Weibull
WEIBULL	Yes	Extreme value

INITIAL=values

sets initial values for the regression parameters. This option can be helpful in the case of convergence difficulty. Specified values are used to initialize the regression coefficients for the covariates specified in the MODEL statement. The intercept parameter is initialized with the INTERCEPT= option and is not included here. The values are assigned to the variables in the MODEL statement in the same order in which they are listed in the MODEL statement. Note that a CLASS variable requires 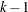$\text{[math]}$ values when the CLASS variable takes on 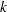$\text{[math]}$ different levels. The order of the CLASS levels is determined by the ORDER= option. If there is no intercept term, the first CLASS variable requires 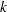$\text{[math]}$ initial values. If a BY statement is used, all CLASS variables must take on the same number of levels in each BY group or no meaningful initial values can be specified. The INITIAL= option can be specified as follows.

Type of List		Specification
List separated by blanks		`initial=3 4 5`
List separated by commas		`initial=3,4,5`
x to y		`initial=3 to 5`
x to y by z		`initial=3 to 5 by 1`
Combination of methods		`initial=1,3 to 5,9`

By default, PROC LIFEREG computes initial estimates with ordinary least squares. See the section Computational Method for details.

Note: The INITIAL= option is overwritten by the INEST= option. See the section INEST= Data Set for details.

INTERCEPT=value

initializes the intercept term to value. By default, the intercept is initialized by an ordinary least squares estimate.

ITPRINT

displays the iteration history for computing maximum likelihood estimates, the final evaluation of the gradient, and the final evaluation of the negative of the second derivative matrix—that is, the negative of the Hessian. If you perform a Bayesian analysis by specifying the BAYES statement, the iteration history for computing the mode of the posterior distribution is also displayed.

MAXITER=n

sets the maximum allowable number of iterations during the model estimation. By default, MAXITER=50.

NOINT

holds the intercept term fixed. Because of the usual log transformation of the response, the intercept parameter is usually a scale parameter for the untransformed response, or a location parameter for a transformed response.

NOLOG

requests that no log transformation of the response variable be performed. By default, PROC LIFEREG models the log of the response variable for the GAMMA, LLOGISTIC, LOGNORMAL, and WEIBULL distribution options. NOLOG is implicitly assumed for the NORMAL and LOGISTIC distribution options.

NOSCALE

holds the scale parameter fixed. Note that if the log transformation has been applied to the response, the effect of the scale parameter is a power transformation of the original response. If no SCALE= value is specified, the scale parameter is fixed at the value 1.

NOSHAPE1

holds the first shape parameter, SHAPE1, fixed. If no SHAPE1= value is specified, SHAPE1 is fixed at a value that depends on the DISTRIBUTION type.

OFFSET=variable

specifies a variable in the input data set to be used as an offset variable. This variable cannot be a CLASS variable, and it cannot be the response variable or one of the explanatory variables.

SCALE=value

initializes the scale parameter to value. If the Weibull distribution is specified, this scale parameter is the scale parameter of the type 1 extreme-value distribution, not the Weibull scale parameter. Note that, with a log transformation, the exponential model is the same as a Weibull model with the scale parameter fixed at the value 1.

SHAPE1=value

initializes the first shape parameter to value. If the specified distribution does not depend on this parameter, then this option has no effect. The only distribution that depends on this shape parameter is the generalized gamma distribution. See the section Supported Distributions for descriptions of the parameterizations of the distributions.

SINGULAR=value

sets the tolerance for testing singularity of the information matrix and the crossproducts matrix for the initial least squares estimates. Roughly, the test requires that a pivot be at least this value times the original diagonal value. By default, SINGULAR=1E $\text{[math]}$ 12.