The ENTROPY Procedure (Experimental)
- Overview
-
Getting Started

-
Syntax

-
Details
 Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics
Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics -
Examples

- References
Multinomial discrete choice models take the form of an experiment that consists of n trials. On each trial, one of k alternatives is observed. If ![]() is the random variable that takes on the value 1 when alternative j is selected for the ith trial and 0 otherwise, then the probability that
is the random variable that takes on the value 1 when alternative j is selected for the ith trial and 0 otherwise, then the probability that ![]() is 1, conditional on a vector of regressors
is 1, conditional on a vector of regressors ![]() and unknown parameter vector
and unknown parameter vector ![]() , is
, is
where ![]() is a link function. For noisy data the model becomes:
is a link function. For noisy data the model becomes:
The standard maximum likelihood approach for multinomial logit is equivalent to the maximum entropy solution for discrete
choice models. The generalized maximum entropy approach avoids an assumption of the form of the link function ![]() .
.
The generalized maximum entropy for discrete choice models (GME-D) is written in primal form as
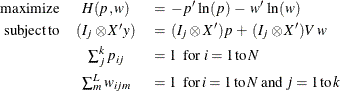
Golan, Judge, and Miller (1996) have shown that the dual unconstrained formulation of the GME-D can be viewed as a general class of logit models. Additionally, as the sample size increases, the solution of the dual problem approaches the maximum likelihood solution. Because of these characteristics, only the dual approach is available for the GME-D estimation method.
The parameters ![]() are the Lagrange multipliers of the constraints. The covariance matrix of the parameter estimates is computed as the inverse
of the Hessian of the dual form of the objective function.
are the Lagrange multipliers of the constraints. The covariance matrix of the parameter estimates is computed as the inverse
of the Hessian of the dual form of the objective function.