The ENTROPY Procedure (Experimental)
- Overview
-
Getting Started

-
Syntax

-
Details
 Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics
Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics -
Examples

- References
Subsections:
- Generalized Maximum Entropy
- Generalized Cross Entropy
- Moment Generalized Maximum Entropy
- Maximum Entropy-Based Seemingly Unrelated Regression
- Generalized Maximum Entropy for Multinomial Discrete Choice Models
- Censored or Truncated Dependent Variables
- Information Measures
- Parameter Covariance For GCE
- Parameter Covariance For GCE-M
- Statistical Tests
- Missing Values
- Input Data Sets
- Output Data Sets
- ODS Table Names
- ODS Graphics
Shannon’s measure of entropy for a distribution is given by
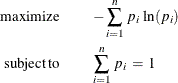
where ![]() is the probability associated with the ith support point. Properties that characterize the entropy measure are set forth by Kapur and Kesavan (1992).
is the probability associated with the ith support point. Properties that characterize the entropy measure are set forth by Kapur and Kesavan (1992).
The objective is to maximize the entropy of the distribution with respect to the probabilities ![]() and subject to constraints that reflect any other known information about the distribution (Jaynes, 1957). This measure, in the absence of additional information, reaches a maximum when the probabilities are uniform. A distribution
other than the uniform distribution arises from information already known.
and subject to constraints that reflect any other known information about the distribution (Jaynes, 1957). This measure, in the absence of additional information, reaches a maximum when the probabilities are uniform. A distribution
other than the uniform distribution arises from information already known.