The ENTROPY Procedure (Experimental)
- Overview
-
Getting Started

-
Syntax

-
Details
 Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics
Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics -
Examples

- References
In a multivariate regression model, the errors in different equations might be correlated. In this case, the efficiency of the estimation can be improved by taking these cross-equation correlations into account. Seemingly unrelated regression (SUR), also called joint generalized least squares (JGLS) or Zellner estimation, is a generalization of OLS for multi-equation systems.
Like SUR in the least squares setting, the generalized maximum entropy SUR (GME-SUR) method assumes that all the regressors are independent variables and uses the correlations among the errors in different equations to improve the regression estimates. The GME-SUR method requires an initial entropy regression to compute residuals. The entropy residuals are used to estimate the cross-equation covariance matrix.
In the iterative GME-SUR (ITGME-SUR) case, the preceding process is repeated by using the residuals from the GME-SUR estimation to estimate a new cross-equation covariance matrix. ITGME-SUR method alternates between estimating the system coefficients and estimating the cross-equation covariance matrix until the estimated coefficients and covariance matrix converge.
The estimation problem becomes the generalized maximum entropy system adapted for multi-equations as follows:
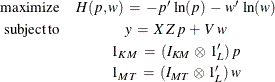
where
![\[ \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \ \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! Z \: = \: \left[ \begin{array}{ccccccccccccccc} z_{11}^{1} & \cdot \cdot \cdot & z_{L1}^{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \ddots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & z_{11}^{K} & \cdot \cdot \cdot & z_{L1}^{K} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddots & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & z_{1M}^{1} & \cdot \cdot \cdot & z_{LM}^{1} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddots & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & z_{1M}^{K} & \cdot \cdot \cdot & z_{LM}^{K} \end{array} \right] \]](images/etsug_entropy0083.png)
![\[ \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \ \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! V \: = \: \left[ \begin{array}{ccccccccccccccc} v_{11}^{1} & \cdot \cdot \cdot & v_{11}^{L} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \ddots & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & v_{1T}^{1} & \cdot \cdot \cdot & v_{1T}^{L} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddots & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & v_{M1}^{1} & \cdot \cdot \cdot & v_{M1}^{L} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \ddots & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & v_{MT}^{1} & \cdot \cdot \cdot & v_{MT}^{L} \end{array} \right] \]](images/etsug_entropy0086.png)
y denotes the MT column vector of observations of the dependent variables; ![]() denotes the (MT x KM ) matrix of observations for the independent variables; p denotes the LKM column vector of weights associated with the points in Z; w denotes the LMT column vector of weights associated with the points in V;
denotes the (MT x KM ) matrix of observations for the independent variables; p denotes the LKM column vector of weights associated with the points in Z; w denotes the LMT column vector of weights associated with the points in V; ![]() ,
, ![]() , and
, and ![]() are L-, KM-, and MT-dimensional column vectors, respectively, of ones; and
are L-, KM-, and MT-dimensional column vectors, respectively, of ones; and ![]() and
and ![]() are (KM x KM) and (MT x MT) dimensional identity matrices. The subscript l denotes the support point
are (KM x KM) and (MT x MT) dimensional identity matrices. The subscript l denotes the support point ![]() , k denotes the parameter
, k denotes the parameter ![]() , m denotes the equation
, m denotes the equation ![]() , and t denotes the observation
, and t denotes the observation ![]() .
.
Using this notation, the maximum entropy problem that is analogous to the OLS problem used as the initial step of the traditional SUR approach is
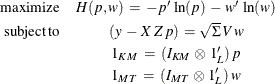
The results are GME-SUR estimates with independent errors, the analog of OLS. The covariance matrix ![]() is computed based on the residual of the equations,
is computed based on the residual of the equations, ![]() . An
. An ![]() factorization of the
factorization of the ![]() is used to compute the square root of the matrix.
is used to compute the square root of the matrix.
After solving this problem, these entropy-based estimates are analogous to the Aitken two-step estimator. For iterative GME-SUR,
the covariance matrix of the errors is recomputed, and a new ![]() is computed and factored. As in traditional ITSUR, this process repeats until the covariance matrix and the parameter estimates
converge.
is computed and factored. As in traditional ITSUR, this process repeats until the covariance matrix and the parameter estimates
converge.
The estimation of the parameters for the normed-moment version of SUR (GME-SUR-NM) uses an identical process. The constraints for GME-SUR-NM is defined as:
The estimation of the parameters for GME-SUR-NM uses an identical process as outlined previously for GME-SUR.