The ENTROPY Procedure (Experimental)
- Overview
-
Getting Started

-
Syntax

-
Details
 Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics
Generalized Maximum EntropyGeneralized Cross EntropyMoment Generalized Maximum EntropyMaximum Entropy-Based Seemingly Unrelated RegressionGeneralized Maximum Entropy for Multinomial Discrete Choice ModelsCensored or Truncated Dependent VariablesInformation MeasuresParameter Covariance For GCEParameter Covariance For GCE-MStatistical TestsMissing ValuesInput Data SetsOutput Data SetsODS Table NamesODS Graphics -
Examples

- References
The default estimation technique is moment generalized maximum entropy (GME-M). This is simply GME with the data constraints
modified by multiplying both sides by ![]() . GME-M then becomes
. GME-M then becomes
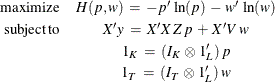
There is also the cross entropy version of GME-M, which has the same form as GCE but with the moment constraints.
GME-M is more computationally attractive than GME for large data sets because the computational complexity of the estimation problem depends primarily on the number of parameters and not on the number of observations. GME-M is based on the first moment of the data, whereas GME is based on the data itself. If the distribution of the residuals is well defined by its first moment, then GME-M is a good choice. So if the residuals are normally distributed or exponentially distributed, then GME-M should be used. On the other hand if the distribution is Cauchy, lognormal, or some other distribution where the first moment does not describe the distribution, then use GME. See Example 13.1 for an illustration of this point.