The HPSEVERITY Procedure
- Overview
-
Getting Started
-
Syntax
-
DetailsPredefined DistributionsCensoring and TruncationParameter Estimation MethodDetails of Optimization AlgorithmsParameter InitializationEstimating Regression EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDistributed and Multithreaded ComputationDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsCustom Objective FunctionsInput Data SetsOutput Data SetsDisplayed Output
-
ExamplesDefining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataBenefits of Distributed and Multithreaded ComputingEstimating Parameters Using Cramér-von Mises Estimator
- References
PROC HPSEVERITY accepts DATA= and INEST= data sets as input data sets. This section details the information they are expected to contain.
The DATA= data set is expected to contain the values of the analysis variables specified in the LOSS statement and the SCALEMODEL statement.
The INEST= data set is expected to contain the initial values of the parameters for the parameter estimation process. The data set must contain the following variables:
- _MODEL_
-
identifying name of the distribution for which the estimates are provided.
- _TYPE_
-
type of the estimate. The value of this variable must be EST for an observation to be valid.
- <Parameter 1> …<Parameter M>
-
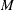variables, named after the parameters of all candidate distributions, that contain initial values of the respective parameters.
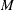is the cardinality of the union of parameter name sets from all candidate distributions. In an observation, estimates are
read only from variables for parameters that correspond to the distribution specified by the _MODEL_ variable.
If you specify a missing value for some parameters, then default initial values are used unless the parameter is initialized by using the INIT= option in the DIST statement. If you want to use the dist_PARMINIT subroutine for initializing the parameters of a model, then you should either not specify the model in the INEST= data set or specify missing values for all the distribution parameters in the INEST= data set and not use the INIT= option in the DIST statement.
If regressors are specified, then the initial value provided for the first parameter of each distribution must be the base value of the scale or log-transformed scale parameter. For more information, see the section Estimating Regression Effects.
- <Regressor 1> …<Regressor K>
-
If
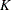regressors are specified in the SCALEMODEL statement, then the INEST= data set must contain 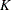variables that are named for each regressor. The variables contain initial values of the respective regression coefficients.
If a regressor is linearly dependent on other regressors, then you can indicate this by providing a special missing value
of .R for the respective variable. If a variable is marked as linearly dependent for one model, then it must be marked so
for all the models. Similarly, if a variable is not marked as linearly dependent for one model, then it must be marked so
for all the models.