The HPSEVERITY Procedure

Defining a Severity Distribution Model with the FCMP Procedure

A severity distribution model consists of a set of functions and subroutines that are defined using the FCMP procedure. The FCMP procedure is part of Base SAS software. Each function or subroutine must be named as distribution-name_keyword, where distribution-name is the identifying short name of the distribution and keyword identifies one of the functions or subroutines. The total length of the name should not exceed 32. Each function or subroutine must have a specific signature, which consists of the number of arguments, sequence and types of arguments, and return value type. The summary of all the recognized function and subroutine names and their expected behavior is given in Table 5.6.

Consider the following points when you define a distribution model:

When you define a function or subroutine requiring parameter arguments, the names and order of those arguments must be the same. Arguments other than the parameter arguments can have any name, but they must satisfy the requirements on their type and order.
When the HPSEVERITY procedure invokes any function or subroutine, it provides the necessary input values according to the specified signature, and expects the function or subroutine to prepare the output and return it according to the specification of the return values in the signature.
You can use most of the SAS programming statements and SAS functions that you can use in a DATA step for defining the FCMP functions and subroutines. However, there are a few differences in the capabilities of the DATA step and the FCMP procedure. To learn more, see the documentation of the FCMP procedure in the Base SAS Procedures Guide.
You must specify either the PDF or the LOGPDF function. Similarly, you must specify either the CDF or the LOGCDF function. All other functions are optional, except when necessary for correct definition of the distribution. It is strongly recommended that you define the PARMINIT subroutine to provide a good set of initial values for the parameters. The information provided by PROC HPSEVERITY to the PARMINIT subroutine enables you to use popular initialization approaches based on the method of moments and the method of percentile matching, but you can implement any algorithm to initialize the parameters by using the values of the response variable and the estimate of its empirical distribution function.
The LOWERBOUNDS subroutines should be defined if the lower bound on at least one distribution parameter is different from the default lower bound of 0. If you define a LOWERBOUNDS subroutine but do not set a lower bound for some parameter inside the subroutine, then that parameter is assumed to have no lower bound (or a lower bound of 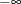$-\infty$ ). Hence, it is recommended that you explicitly return the lower bound for each parameter when you define the LOWERBOUNDS subroutine.
The UPPERBOUNDS subroutines should be defined if the upper bound on at least one distribution parameter is different from the default upper bound of 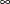$\infty$ . If you define an UPPERBOUNDS subroutine but do not set an upper bound for some parameter inside the subroutine, then that parameter is assumed to have no upper bound (or a upper bound of 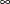$\infty$ ). Hence, it is recommended that you explicitly return the upper bound for each parameter when you define the UPPERBOUNDS subroutine.
If you want to use the distribution in a model with regression effects, then make sure that the first parameter of the distribution is the scale parameter itself or a log-transformed scale parameter. If the first parameter is a log-transformed scale parameter, then you must define the SCALETRANSFORM function.
In general, it is not necessary to define the gradient and Hessian functions, because the HPSEVERITY procedure uses an internal system to evaluate the required derivatives. The internal system typically computes the derivatives analytically. But it might not be able to do so if your function definitions use other functions that it cannot differentiate analytically. In such cases, derivatives are approximated using a finite difference method and a note is written to the SAS log to indicate the components that are differentiated using such approximations. PROC HPSEVERITY does reasonably well with these finite difference approximations. But, if you know of a way to compute the derivatives of such components analytically, then you should define the gradient and Hessian functions.

In order to use your distribution with PROC HPSEVERITY, you need to record the FCMP library that contains the functions and subroutines for your distribution and other FCMP libraries that contain FCMP functions or subroutines used within your distribution’s functions and subroutines. Specify all those libraries in the CMPLIB= system option by using the OPTIONS global statement. For more information about the OPTIONS statement, see SAS Statements: Reference. For more information about the CMPLIB= system option, see SAS System Options: Reference.

Each predefined distribution mentioned in the section Predefined Distributions has a distribution model associated with it. The functions and subroutines of all those models are available in the Sashelp.Svrtdist library. The order of the parameters in the signatures of the functions and subroutines is the same as listed in Table 5.2. You do not need to use the CMPLIB= option in order to use the predefined distributions with PROC HPSEVERITY. However, if you need to use the functions or subroutines of the predefined distributions in SAS statements other than the PROC HPSEVERITY step (such as in a DATA step), then specify the Sashelp.Svrtdist library in the CMPLIB= system option by using the OPTIONS global statement prior to using them.

Table 5.6 shows functions and subroutines that define a distribution model, and subsections after the table provide more detail. The functions are listed in alphabetical order of the keyword suffix.

Table 5.6: List of Functions and Subroutines That Define a Distribution Model

Name	Type	Required	Expected to Return
dist_CDF	Function	YES	Cumulative distribution
			function value
dist_CDFGRADIENT	Subroutine	NO	Gradient of the CDF
dist_CDFHESSIAN	Subroutine	NO	Hessian of the CDF
dist_CONSTANTPARM	Subroutine	NO	Constant parameters
dist_DESCRIPTION	Function	NO	Description of the distribution
dist_LOGCDF	Function	YES	Log of cumulative distribution
			function value
dist_LOGCDFGRADIENT	Subroutine	NO	Gradient of the LOGCDF
dist_LOGCDFHESSIAN	Subroutine	NO	Hessian of the LOGCDF
dist_LOGPDF	Function	YES	Log of probability density
			function value
dist_LOGPDFGRADIENT	Subroutine	NO	Gradient of the LOGPDF
dist_LOGPDFHESSIAN	Subroutine	NO	Hessian of the LOGPDF
dist_LOGSDF	Function	NO	Log of survival
			function value
dist_LOGSDFGRADIENT	Subroutine	NO	Gradient of the LOGSDF
dist_LOGSDFHESSIAN	Subroutine	NO	Hessian of the LOGSDF
dist_LOWERBOUNDS	Subroutine	NO	Lower bounds on parameters
dist_PARMINIT	Subroutine	NO	Initial values
			for parameters
dist_PDF	Function	YES	Probability density
			function value
dist_PDFGRADIENT	Subroutine	NO	Gradient of the PDF
dist_PDFHESSIAN	Subroutine	NO	Hessian of the PDF
dist_SCALETRANSFORM	Function	NO	Type of relationship between
			the first distribution parameter
			and the scale parameter
dist_SDF	Function	NO	Survival function value
dist_SDFGRADIENT	Subroutine	NO	Gradient of the SDF
dist_SDFHESSIAN	Subroutine	NO	Hessian of the SDF
dist_UPPERBOUNDS	Subroutine	NO	Upper bounds on parameters
Notes:
1. Either the dist_CDF or the dist_LOGCDF function must be defined.
2. Either the dist_PDF or the dist_LOGPDF function must be defined.

The signature syntax and semantics of each function or subroutine are as follows:

dist_CDF

defines a function that returns the value of the cumulative distribution function (CDF) of the distribution at the specified values of the random variable and distribution parameters.

Type: Function
Required: YES
Number of arguments: , where is the number of distribution parameters
Sequence and type of arguments:

x

Numeric value of the random variable at which the CDF value should be evaluated

p1

Numeric value of the first parameter

p2

Numeric value of the second parameter …..

p

Numeric value of the th parameter
Return value: Numeric value that contains the CDF value $F(x; p_1, p_2, \dotsc , p_ m)$

If you want to consider this distribution as a candidate distribution when you estimate a response variable model with regression effects, then the first parameter of this distribution must be a scale parameter or log-transformed scale parameter. In other words, if the distribution has a scale parameter, then the following equation must be satisfied:

$F(x; p_1, p_2, \dotsc , p_ m) = F(\frac{x}{p_1}; 1, p_2, \dotsc , p_ m)$

If the distribution has a log-transformed scale parameter, then the following equation must be satisfied:

$F(x; p_1, p_2, \dotsc , p_ m) = F(\frac{x}{\exp (p_1)}; 0, p_2, \dotsc , p_ m)$

Here is a sample structure of the function for a distribution named 'FOO':

    function FOO_CDF(x, P1, P2);
        /* Code to compute CDF by using x, P1, and P2 */

        F = <computed CDF>;
        return (F);
    endsub;

dist_CONSTANTPARM

defines a subroutine that specifies constant parameters. A parameter is constant if it is required for defining a distribution but is not subject to optimization in PROC HPSEVERITY. Constant parameters are required to be part of the model in order to compute the PDF or the CDF of the distribution. Typically, values of these parameters are known a priori or estimated using some means other than the maximum likelihood method used by PROC HPSEVERITY. You can estimate them inside the dist_PARMINIT subroutine. Once initialized, the parameters remain constant in the context of PROC HPSEVERITY; that is, they retain their initial value. PROC HPSEVERITY estimates only the nonconstant parameters.

Type: Subroutine
Required: NO
Number of arguments: , where is the number of constant parameters
Sequence and type of arguments:

constant parameter 1

Name of the first constant parameter …..

constant parameter

Name of the th constant parameter
Return value: None

Here is a sample structure of the subroutine for a distribution named 'FOO' that has P3 and P5 as its constant parameters, assuming that distribution has at least three parameters:

    subroutine FOO_CONSTANTPARM(p5, p3);
    endsub;

Note the following points when you specify the constant parameters:

At least one distribution parameter must be free to be optimized; that is, if a distribution has total parameters, then must be strictly less than .
If you want to use this distribution for modeling regression effects, then the first parameter must not be a constant parameter.
The order of arguments in the signature of this subroutine does not matter as long as each argument’s name matches the name of one of the parameters that are defined in the signature of the dist_PDF function.
The constant parameters must be specified in signatures of all the functions and subroutines that accept distribution parameters as their arguments.
You must provide a nonmissing initial value for each constant parameter by using one of the supported parameter initialization methods.

dist_DESCRIPTION

defines a function that returns a description of the distribution.

Type: Function
Required: NO
Number of arguments: None
Sequence and type of arguments: Not applicable
Return value: Character value containing a description of the distribution

Here is a sample structure of the function for a distribution named 'FOO':

    function FOO_DESCRIPTION() $48;
        length desc $48;
        desc = "A model for a continuous distribution named foo";
        return (desc);
    endsub;

There is no restriction on the length of the description (the length of 48 used in the previous example is for illustration purposes only). However, if the length is greater than 256, then only the first 256 characters appear in the displayed output and in the _DESCRIPTION_ variable of the OUTMODELINFO= data set. Hence, the recommended length of the description is less than or equal to 256.

dist_LOGcore

defines a function that returns the natural logarithm of the specified core function of the distribution at the specified values of the random variable and distribution parameters. The core keyword can be PDF, CDF, or SDF.

Type: Function
Required: YES only if core is PDF or CDF and you have not defined that core function; otherwise, NO
Number of arguments: , where is the number of distribution parameters
Sequence and type of arguments:

x

Numeric value of the random variable at which the natural logarithm of the core function should be evaluated

p1

Numeric value of the first parameter

p2

Numeric value of the second parameter …..

p

Numeric value of the th parameter
Return value: Numeric value that contains the natural logarithm of the core function

Here is a sample structure of the function for the core function PDF of a distribution named 'FOO':

    function FOO_LOGPDF(x, P1, P2);
        /* Code to compute LOGPDF by using x, P1, and P2 */

        l = <computed LOGPDF>;
        return (l);
    endsub;

dist_LOWERBOUNDS

defines a subroutine that returns lower bounds for the parameters of the distribution. If this subroutine is not defined for a given distribution, then the HPSEVERITY procedure assumes a lower bound of 0 for each parameter. If a lower bound of is returned for a parameter , then the HPSEVERITY procedure assumes that (strict inequality). If a missing value is returned for some parameter, then the HPSEVERITY procedure assumes that there is no lower bound for that parameter (equivalent to a lower bound of $-\infty$ ).

Type: Subroutine
Required: NO
Number of arguments: , where is the number of distribution parameters
Sequence and type of arguments:

p1

Output argument that returns the lower bound on the first parameter. This must be specified in the OUTARGS statement inside the subroutine’s definition.

p2

Output argument that returns the lower bound on the second parameter. This must be specified in the OUTARGS statement inside the subroutine’s definition. …..

p

Output argument that returns the lower bound on the th parameter. This must be specified in the OUTARGS statement inside the subroutine’s definition.
Return value: The results, lower bounds on parameter values, should be returned in the parameter arguments of the subroutine.

Here is a sample structure of the subroutine for a distribution named 'FOO':

    subroutine FOO_LOWERBOUNDS(p1, p2);
        outargs p1, p2;

        p1 = <lower bound for P1>;
        p2 = <lower bound for P2>;
    endsub;

dist_PARMINIT

defines a subroutine that returns the initial values for the distribution’s parameters given an empirical distribution function (EDF) estimate.

Type: Subroutine
Required: NO
Number of arguments: , where is the number of distribution parameters
Sequence and type of arguments:

dim

Input numeric value that contains the dimension of the x, nx, and F array arguments.

x{*}

Input numeric array of dimension dim that contains values of the random variables at which the EDF estimate is available. It can be assumed that x contains values in an increasing order. In other words, if , then x[] x[].

nx{*}

Input numeric array of dimension dim. Each nx[] contains the number of observations in the original data that have the value x[].

F{*}

Input numeric array of dimension dim. Each F[] contains the EDF estimate for x[]. This estimate is computed by the HPSEVERITY procedure based on the options specified in the LOSS statement.

Ftype

Input numeric value that contains the type of the EDF estimate that is stored in x and F. See the section Supplying EDF Estimates to Functions and Subroutines for definition of types.

p1

Output argument that returns the initial value of the first parameter. This must be specified in the OUTARGS statement inside the subroutine’s definition.

p2

Output argument that returns the initial value of the second parameter. This must be specified in the OUTARGS statement inside the subroutine’s definition. …..

p

Output argument that returns the initial value of the th parameter. This must be specified in the OUTARGS statement inside the subroutine’s definition.
Return value: The results, initial values of the parameters, should be returned in the parameter arguments of the subroutine.

Here is a sample structure of the subroutine for a distribution named 'FOO':

    subroutine FOO_PARMINIT(dim, x{*}, nx{*}, F{*}, Ftype, p1, p2);
        outargs p1, p2;

        /* Code to initialize values of P1 and P2 by using
           dim, x, nx, and F */

        p1 = <initial value for p1>;
        p2 = <initial value for p2>;
    endsub;

dist_PDF

defines a function that returns the value of the probability density function (PDF) of the distribution at the specified values of the random variable and distribution parameters.

Type: Function
Required: YES
Number of arguments: , where is the number of distribution parameters
Sequence and type of arguments:

x

Numeric value of the random variable at which the PDF value should be evaluated

p1

Numeric value of the first parameter

p2

Numeric value of the second parameter …..

p

Numeric value of the th parameter
Return value: Numeric value that contains the PDF value $f(x; p_1, p_2, \dotsc , p_ m)$

$f(x; p_1, p_2, \dotsc , p_ m) = \frac{1}{p_1} f(\frac{x}{p_1}; 1, p_2, \dotsc , p_ m)$

If the distribution has a log-transformed scale parameter, then the following equation must be satisfied:

$f(x; p_1, p_2, \dotsc , p_ m) = \frac{1}{\exp (p_1)} f(\frac{x}{\exp (p_1)}; 0, p_2, \dotsc , p_ m)$

Here is a sample structure of the function for a distribution named 'FOO':

    function FOO_PDF(x, P1, P2);
        /* Code to compute PDF by using x, P1, and P2 */

        f = <computed PDF>;
        return (f);
    endsub;

dist_SCALETRANSFORM

defines a function that returns a keyword to identify the transform that needs to be applied to the scale parameter to convert it to the first parameter of the distribution.

If you want to use this distribution for modeling regression effects, then the first parameter of this distribution must be a scale parameter. However, for some distributions, a typical or convenient parameterization might not have a scale parameter, but one of the parameters can be a simple transform of the scale parameter. As an example, consider a typical parameterization of the lognormal distribution with two parameters, location $\mu$ and shape $\sigma$ , for which the PDF is defined as follows:

$f(x; \mu , \sigma ) = \frac{1}{x \sigma \sqrt {2 \pi }} e^{-\frac{1}{2}\left(\frac{\log (x)-\mu }{\sigma }\right)^2}$

You can reparameterize this distribution to contain a parameter $\theta$ instead of the parameter $\mu$ such that $\mu = \log (\theta )$ . The parameter $\theta$ would then be a scale parameter. However, if you want to specify the distribution in terms of $\mu$ and $\sigma$ (which is a more recognized form of the lognormal distribution) and still allow it as a candidate distribution for estimating regression effects, then instead of writing another distribution with parameters $\theta$ and $\sigma$ , you can simply define the distribution with $\mu$ as the first parameter and specify that it is the logarithm of the scale parameter.

Type: Function
Required: NO
Number of arguments: None
Sequence and type of arguments: Not applicable
Return value: Character value that contains one of the following keywords:

LOG

specifies that the first parameter is the logarithm of the scale parameter.

IDENTITY

specifies that the first parameter is a scale parameter without any transformation.

If this function is not specified, then the IDENTITY transform is assumed.

Here is a sample structure of the function for a distribution named 'FOO':

    function FOO_SCALETRANSFORM() $8;
        length xform $8;
        xform = "IDENTITY";
        return (xform);
    endsub;

dist_SDF

defines a function that returns the value of the survival distribution function (SDF) of the distribution at the specified values of the random variable and distribution parameters.

Type: Function
Required: NO
Number of arguments: , where is the number of distribution parameters
Sequence and type of arguments:

x

Numeric value of the random variable at which the SDF value should be evaluated

p1

Numeric value of the first parameter

p2

Numeric value of the second parameter …..

p

Numeric value of the th parameter
Return value: Numeric value that contains the SDF value $S(x; p_1, p_2, \dotsc , p_ m)$

If you want to consider this distribution as a candidate distribution when estimating a response variable model with regression effects, then the first parameter of this distribution must be a scale parameter or log-transformed scale parameter. In other words, if the distribution has a scale parameter, then the following equation must be satisfied:

$S(x; p_1, p_2, \dotsc , p_ m) = S(\frac{x}{p_1}; 1, p_2, \dotsc , p_ m)$

If the distribution has a log-transformed scale parameter, then the following equation must be satisfied:

$S(x; p_1, p_2, \dotsc , p_ m) = S(\frac{x}{\exp (p_1)}; 0, p_2, \dotsc , p_ m)$

Here is a sample structure of the function for a distribution named 'FOO':

    function FOO_SDF(x, P1, P2);
        /* Code to compute SDF by using x, P1, and P2 */

        S = <computed SDF>;
        return (S);
    endsub;

dist_UPPERBOUNDS

defines a subroutine that returns upper bounds for the parameters of the distribution. If this subroutine is not defined for a given distribution, then the HPSEVERITY procedure assumes that there is no upper bound for any of the parameters. If an upper bound of is returned for a parameter , then the HPSEVERITY procedure assumes that (strict inequality). If a missing value is returned for some parameter, then the HPSEVERITY procedure assumes that there is no upper bound for that parameter (equivalent to an upper bound of $\infty$ ).

Type: Subroutine
Required: NO
Number of arguments: , where is the number of distribution parameters
Sequence and type of arguments:

p1

Output argument that returns the upper bound on the first parameter. This must be specified in the OUTARGS statement inside the subroutine’s definition.

p2

Output argument that returns the upper bound on the second parameter. This must be specified in the OUTARGS statement inside the subroutine’s definition. …..

p

Output argument that returns the upper bound on the th parameter. This must be specified in the OUTARGS statement inside the subroutine’s definition.
Return value: The results, upper bounds on parameter values, should be returned in the parameter arguments of the subroutine.

Here is a sample structure of the subroutine for a distribution named 'FOO':

    subroutine FOO_UPPERBOUNDS(p1, p2);
        outargs p1, p2;

        p1 = <upper bound for P1>;
        p2 = <upper bound for P2>;
    endsub;

dist_coreGRADIENT

defines a subroutine that returns the gradient vector of the specified core function of the distribution at the specified values of the random variable and distribution parameters. The core keyword can be PDF, CDF, SDF, LOGPDF, LOGCDF, or LOGSDF.

Type: Subroutine
Required: NO
Number of arguments: , where is the number of distribution parameters
Sequence and type of arguments:

x

Numeric value of the random variable at which the gradient should be evaluated

p1

Numeric value of the first parameter

p2

Numeric value of the second parameter …..

p

Numeric value of the th parameter

grad{*}

Output numeric array of size that contains the gradient vector evaluated at the specified values. If denotes the value of the core function, then the expected order of the values in the array is as follows: $\frac{\partial h}{\partial p_1} \; \frac{\partial h}{\partial p_2} \cdots \frac{\partial h}{\partial p_ m}$
Return value: Numeric array that contains the gradient evaluated at for the parameter values $(p_1, p_2, \dotsc , p_ m)$

Here is a sample structure of the function for the core function CDF of a distribution named 'FOO':

    subroutine FOO_CDFGRADIENT(x, P1, P2, grad{*});
        outargs grad;

        /* Code to compute gradient by using x, P1, and P2 */
        grad[1] = <partial derivative of CDF w.r.t. P1
                   evaluated at x, P1, P2>;
        grad[2] = <partial derivative of CDF w.r.t. P2
                   evaluated at x, P1, P2>;
    endsub;

dist_coreHESSIAN

defines a subroutine that returns the Hessian matrix of the specified core function of the distribution at the specified values of the random variable and distribution parameters. The core keyword can be PDF, CDF, SDF, LOGPDF, LOGCDF, or LOGSDF.

Type: Subroutine
Required: NO
Number of arguments: , where is the number of distribution parameters
Sequence and type of arguments:

x

Numeric value of the random variable at which the Hessian matrix should be evaluated

p1

Numeric value of the first parameter

p2

Numeric value of the second parameter …..

p

Numeric value of the th parameter

hess{*}

Output numeric array of size that contains the lower triangular portion of the Hessian matrix in a packed vector form, evaluated at the specified values. If denotes the value of the core function, then the expected order of the values in the array is as follows: $\frac{\partial ^2 h}{\partial p_1^2} \, | \, \frac{\partial ^2 h}{\partial p_1 \partial p_2} \; \frac{\partial ^2 h}{\partial p_2^2} \, | \cdots | \, \frac{\partial ^2 h}{\partial p_1 \partial p_ m} \; \frac{\partial ^2 h}{\partial p_2 \partial p_ m} \cdots \frac{\partial ^2 h}{\partial p_ m^2}$
Return value: Numeric array that contains the lower triangular portion of the Hessian matrix evaluated at for the parameter values $(p_1, p_2, \dotsc , p_ m)$

Here is a sample structure of the subroutine for the core function LOGSDF of a distribution named 'FOO':

    subroutine FOO_LOGSDFHESSIAN(x, P1, P2, hess{*});
        outargs hess;

        /* Code to compute Hessian by using x, P1, and P2 */
        hess[1] = <second order partial derivative of LOGSDF
                   w.r.t. P1 evaluated at x, P1, P2>;
        hess[2] = <second order partial derivative of LOGSDF
                   w.r.t. P1 and P2 evaluated at x, P1, P2>;
        hess[3] = <second order partial derivative of LOGSDF
                   w.r.t. P2 evaluated at x, P1, P2>;
    endsub;