Censoring and Truncation
Previous Page|Next Page

The HPSEVERITY Procedure

Censoring and Truncation

Truncation and Conditional CDF Estimates

One of the key features of PROC HPSEVERITY is that it enables you to specify whether the severity event’s magnitude is observable and if it is observable, then whether the exact value of the magnitude is known. If an event is unobservable when the magnitude is in certain intervals, then it is referred to as a truncation effect. If the exact magnitude of the event is not known, but it is known to have a value in a certain interval, then it is referred to as a censoring effect.

PROC HPSEVERITY allows a severity event to be subject to any combination of the following four censoring and truncation effects:

  • Left-truncation: An event is said to be left-truncated if it is observed only when 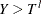$Y > T^ l$, where 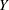$Y$ denotes the random variable for the magnitude and 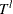$T^ l$ denotes a random variable for the truncation threshold. You can specify left-truncation using the LEFTTRUNCATED= option in the LOSS statement.

  • Right-truncation: An event is said to be right-truncated if it is observed only when 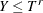$Y \leq T^ r$, where 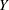$Y$ denotes the random variable for the magnitude and 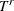$T^ r$ denotes a random variable for the truncation threshold. You can specify right-truncation using the RIGHTTRUNCATED= option in the LOSS statement.

  • Left-censoring: An event is said to be left-censored if it is known that the magnitude is 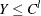$Y \leq C^ l$, but the exact value of 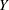$Y$ is not known. 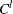$C^ l$ is a random variable for the censoring limit. You can specify left-censoring using the LEFTCENSORED= option in the LOSS statement.

  • Right-censoring: An event is said to be right-censored if it is known that the magnitude is 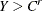$Y > C^ r$, but the exact value of 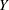$Y$ is not known. 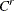$C^ r$ is a random variable for the censoring limit. You can specify right-censoring using the RIGHTCENSORED= option in the LOSS statement.

For each effect, you can specify a different threshold or limit for each observation or specify a single threshold or limit that applies to all the observations.

If all the four types of effects are present on an event, then the following relationship holds: $T^ l < C^ r \leq C^ l \leq T^ r$. PROC HPSEVERITY checks these relationships and write a warning to the SAS log if any is violated.

If the response variable is specified in the LOSS statement, then PROC HPSEVERITY also checks whether each observation satisfies the definitions of the specified censoring and truncation effects. If left-truncation is specified, then PROC HPSEVERITY ignores observations where $Y \leq T^ l$, because such observations are not observable by definition. Similarly, if right-truncation is specified, then PROC HPSEVERITY ignores observations where $Y > T^ r$. If left-censoring is specified, then PROC HPSEVERITY treats an observation with $Y > C^ l$ as uncensored and ignores the value of $C^ l$. The observations with $Y \leq C^ l$ are considered as left-censored, and the value of $Y$ is ignored. If right-censoring is specified, then PROC HPSEVERITY treats an observation with $Y \leq C^ r$ as uncensored and ignores the value of $C^ r$. The observations with $Y > C^ r$ are considered as right-censored, and the value of $Y$ is ignored. The specification of both left-censoring and right-censoring is referred to as interval-censoring. If $C^ r < C^ l$ is satisfied for an observation, then it is considered as interval-censored and the value of the response variable is ignored. If $C^ r = C^ l$ for an observation, then PROC HPSEVERITY assumes that observation to be uncensored. If all the observations in a data set are censored in some form, then the specification of the response variable in the LOSS statement is optional, because the actual value of the response variable is not required for the purposes of estimating a model.

Specification of censoring and truncation affects the likelihood of the data (see the section Likelihood Function) and how the empirical distribution function (EDF) is estimated (see the section Empirical Distribution Function Estimation Methods).

Truncation and Conditional CDF Estimates

If left-truncation or right-truncation is specified, then the EDF estimates that are computed by all methods except the STANDARD method are conditional on the truncation information. See the section EDF Estimates and Truncation for more information. In such cases, PROC HPSEVERITY uses conditional estimates of the CDF when it computes the EDF-based statistics of fit.

Let $t^ l_{\text {min}} = \text {min}_ i \lbrace t^ l_ i \rbrace $ be the smallest value of the left-truncation threshold ($t^ l_ i$ is the left-truncation threshold for observation $i$) and $t^ r_{\text {max}} = \text {max}_ i \lbrace t^ r_ i \rbrace $ be the largest value of the right-truncation threshold ($t^ r_ i$ is the right-truncation threshold for observation $i$). If $\hat{F}(y)$ denotes the unconditional estimate of the CDF at $y$, then the conditional estimate $\hat{F}^ c(y)$ is computed as follows:

  • If an observation is both left-truncated and right-truncated, then

    \[ \hat{F}^ c(y) = \frac{\hat{F}(y) - \hat{F}(t^ l_{\text {min}})}{\hat{F}(t^ r_{\text {max}}) - \hat{F}(t^ l_{\text {min}})} \]

  • If an observation is left-truncated but not right-truncated, then

    \[ \hat{F}^ c(y) = \frac{\hat{F}(y) - \hat{F}(t^ l_{\text {min}})}{1 - \hat{F}(t^ l_{\text {min}})} \]

  • If an observation is right-truncated but not left-truncated, then

    \[ \hat{F}^ c(y) = \frac{\hat{F}(y)}{\hat{F}(t^ r_{\text {max}})} \]

If regressors are specified, then $\hat{F}(y)$, $\hat{F}(t^ l_{\text {min}})$, and $\hat{F}(t^ r_{\text {max}})$ are all computed from a mixture distribution, as described in the section CDF Estimates with Regression Effects.

Previous Page|Next Page|Top of Page
Copyright © SAS Institute Inc. All Rights Reserved.