The MCMC Procedure
-
Overview
-
Getting Started
-
Syntax
-
Details
How PROC MCMC Works Blocking of Parameters Sampling Methods Tuning the Proposal Distribution Conjugate Sampling Initial Values of the Markov Chains Assignments of Parameters Standard Distributions Usage of Multivariate Distributions Specifying a New Distribution Using Density Functions in the Programming Statements Truncation and Censoring Some Useful SAS Functions Matrix Functions in PROC MCMC Create Design Matrix Modeling Joint Likelihood Regenerating Diagnostics Plots Caterpillar Plot Posterior Predictive Distribution Handling of Missing Data Floating Point Errors and Overflows Handling Error Messages Computational Resources Displayed Output ODS Table Names ODS Graphics
-
Examples
Simulating Samples From a Known Density Box-Cox Transformation Logistic Regression Model with a Diffuse Prior Logistic Regression Model with Jeffreys’ Prior Poisson Regression Nonlinear Poisson Regression Models Logistic Regression Random-Effects Model Nonlinear Poisson Regression Random-Effects Model Multivariate Normal Random-Effects Model Change Point Models Exponential and Weibull Survival Analysis Time Independent Cox Model Time Dependent Cox Model Piecewise Exponential Frailty Model Normal Regression with Interval Censoring Constrained Analysis Implement a New Sampling Algorithm Using a Transformation to Improve Mixing Gelman-Rubin Diagnostics
- References
| PARMS Statement |
- PARMS name | ( name-list ) <=> <{> number | number-list <}>
<name | ( name-list ) <=> <{> number | number-list <}> ...>
</ NORMAL | T < (df)> | UDS > ;
The PARMS statement lists the names of the parameters in the model and specifies optional initial values for these parameters. Multiple PARMS statements are allowed. Each PARMS statement defines a block of parameters, and the blocked Metropolis algorithm updates the parameters in each block simultaneously. See the section Blocking of Parameters for more details. PROC MCMC generates missing initial values from the prior distributions whenever needed, as long as they are the standard distributions and not the functions GENERAL or DGENERAL.
If your model contains a multidimensional parameter (for example, a parameter with a multivariate normal prior distribution), the parameter must be declared as an array (using the ARRAY statement). You can use braces 
after the name to assign initial values to the array parameter. For example:
array mu[3];
parms mu {1 2 3};
You cannot assign initial values to the parameter in the ARRAY statement. The following statement assigns three numbers to mu:
array mu[3] (1 2 3);
Array mu now is a constant array and cannot be used as a parameter in the PARMS statement.
Every parameter in the PARMS statement must have a corresponding prior distribution in the PRIOR statement. The program exits if the one-to-one requirement is not satisfied.
The optional arguments give you control over different samplers explicitly for that block of parameters. The normal proposal distribution in the random walk Metropolis is the default. You can also choose a t distribution with df degrees of freedom. If df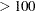 
, the normal distribution is used instead.
The user-defined sampler (UDS) option enables you to implement a new sampler for any of the parameters in the block (see the section UDS Statement). PROC MCMC does not use the Metropolis sampler on these parameters and incorporates your sampler to draw posterior samples. This can sometimes greatly improve the convergence and mixing of the Markov chain. This functionality is for advanced users, and you should proceed with caution.