The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC Works Blocking of Parameters Sampling Methods Tuning the Proposal Distribution Conjugate Sampling Initial Values of the Markov Chains Assignments of Parameters Standard Distributions Usage of Multivariate Distributions Specifying a New Distribution Using Density Functions in the Programming Statements Truncation and Censoring Some Useful SAS Functions Matrix Functions in PROC MCMC Create Design Matrix Modeling Joint Likelihood Regenerating Diagnostics Plots Caterpillar Plot Posterior Predictive Distribution Handling of Missing Data Floating Point Errors and Overflows Handling Error Messages Computational Resources Displayed Output ODS Table Names ODS Graphics
How PROC MCMC Works Blocking of Parameters Sampling Methods Tuning the Proposal Distribution Conjugate Sampling Initial Values of the Markov Chains Assignments of Parameters Standard Distributions Usage of Multivariate Distributions Specifying a New Distribution Using Density Functions in the Programming Statements Truncation and Censoring Some Useful SAS Functions Matrix Functions in PROC MCMC Create Design Matrix Modeling Joint Likelihood Regenerating Diagnostics Plots Caterpillar Plot Posterior Predictive Distribution Handling of Missing Data Floating Point Errors and Overflows Handling Error Messages Computational Resources Displayed Output ODS Table Names ODS Graphics -
Examples
 Simulating Samples From a Known Density Box-Cox Transformation Logistic Regression Model with a Diffuse Prior Logistic Regression Model with Jeffreys’ Prior Poisson Regression Nonlinear Poisson Regression Models Logistic Regression Random-Effects Model Nonlinear Poisson Regression Random-Effects Model Multivariate Normal Random-Effects Model Change Point Models Exponential and Weibull Survival Analysis Time Independent Cox Model Time Dependent Cox Model Piecewise Exponential Frailty Model Normal Regression with Interval Censoring Constrained Analysis Implement a New Sampling Algorithm Using a Transformation to Improve Mixing Gelman-Rubin Diagnostics
Simulating Samples From a Known Density Box-Cox Transformation Logistic Regression Model with a Diffuse Prior Logistic Regression Model with Jeffreys’ Prior Poisson Regression Nonlinear Poisson Regression Models Logistic Regression Random-Effects Model Nonlinear Poisson Regression Random-Effects Model Multivariate Normal Random-Effects Model Change Point Models Exponential and Weibull Survival Analysis Time Independent Cox Model Time Dependent Cox Model Piecewise Exponential Frailty Model Normal Regression with Interval Censoring Constrained Analysis Implement a New Sampling Algorithm Using a Transformation to Improve Mixing Gelman-Rubin Diagnostics - References
| MODEL Statement |
- MODEL dependent-variable-list
 distribution ;
distribution ;
The MODEL statement specifies the conditional distribution of the data given the parameters (the likelihood function). You must specify a single dependent variable or a list of dependent variables, a tilde 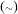 , and then a distribution with its arguments. The dependent variables can be variables from the input data set or functions of the symbols in the program. The dependent variables must be specified unless the functions GENERAL or DGENERAL are used (see the section Specifying a New Distribution for more details). Multiple MODEL statements are allowed for defining models with multiple independent components. The log-likelihood value is the sum of the log-likelihood values from each MODEL statement.
, and then a distribution with its arguments. The dependent variables can be variables from the input data set or functions of the symbols in the program. The dependent variables must be specified unless the functions GENERAL or DGENERAL are used (see the section Specifying a New Distribution for more details). Multiple MODEL statements are allowed for defining models with multiple independent components. The log-likelihood value is the sum of the log-likelihood values from each MODEL statement.
PROC MCMC is a programming language that is similar to the DATA step, and the order of statement evaluation is important. For example, the MODEL statement must come after any SAS programming statements that define or modify arguments used in the construction of the log likelihood. In PROC MCMC, a symbol can be defined multiple times and used at different places. Using an expression out of order produces erroneous results that can also be hard to detect.
Standard distributions that the MODEL statement supports are listed in the Table 54.2 and Table 54.3 (see the section Standard Distributions for density specification). All distributions except the multinomial distribution can be used also in the PRIOR and HYPERPRIOR statements. PROC MCMC allows some distributions to be parameterized in multiple ways. For example, you can specify a normal distribution with a variance (VAR=), standard deviation (SD=), or precision (PRECISION=) parameter. For distributions that have different parameterizations, you must specify an option to clearly name the ambiguous parameter. For example, in the normal distribution, you must indicate whether the second argument represents variance, standard deviation, or precision.
All univariate distributions, with the exception of binary and uniform, can have the optional LOWER= and UPPER= arguments, which specify a truncated density. See the section Truncation and Censoring for more details. Truncation is not supported for multivariate distributions.
Distribution Name |
Definition |
|---|---|
beta(<a=> |
Beta distribution with shape parameters |
binary(<prob|p=> |
Binary (Bernoulli) distribution with probability of success |
binomial (<n=> |
Binomial distribution with count |
cauchy (<location|loc|l=> |
Cauchy distribution with location |
chisq(<df=> |
|
dgeneral(ll) |
General log-likelihood function that you construct using SAS programming statements for single or multiple discrete variables. Also see the function general. The name dlogden is an alias for this function. |
expchisq(<df=> |
Log transformation of a |
Log transformation of an exponential distribution with scale or inverse-scale parameter |
|
expGamma(<shape|sp=> a, scale|s= |
Log transformation of a gamma distribution with shape |
expichisq(<df=> |
Log transformation of an inverse |
expiGamma(<shape|sp=> a, scale|s= |
Log transformation of an inverse-gamma distribution with shape |
expsichisq(<df=> |
Log transformation of a scaled inverse |
Exponential distribution with scale or inverse-scale parameter |
|
gamma(<shape|sp=> a, scale|s= |
Gamma distribution with shape |
geo(<prob|p=> |
Geometric distribution with probability |
general(ll) |
General log-likelihood function that you construct using SAS programming statements for a single or multiple continuous variables. The argument ll is an expression for the log of the distribution. If there are multiple variables specified before the tilde in a MODEL, PRIOR, or HYPERPRIOR statement, ll is interpreted as the log of the joint distribution for these variables. Note that in the MODEL statement, the response variable specified before the tilde is just a place holder and is of no consequence; the variable must have appeared in the construction of ll in the programming statements. general(constant) is equivalent to a uniform distribution on the real line. You can use the alias logden for this distribution. |
ichisq(<df=> |
Inverse |
igamma(<shape|sp=> a, scale|s= |
Inverse-gamma distribution with shape |
laplace(<location|loc|l=> |
Laplace distribution with location |
logistic(<location|loc|l=> |
Logistic distribution with location |
lognormal(<mean|m=> |
Log-normal distribution with mean |
negbin(<n=> |
Negative binomial distribution with count |
normal(<mean|m=> |
Normal (Gaussian) distribution with mean |
pareto(<shape|sp=> |
Pareto distribution with shape |
poisson(<mean|m=> |
Poisson distribution with mean |
sichisq(<df=> |
Scaled inverse |
t(<mean|m=> |
|
uniform(<left|l=> |
Uniform distribution with range |
wald(<mean|m=> |
Wald distribution with mean parameter |
weibull( |
Weibull distribution with location (threshold) parameter |
Distribution Name |
Definition |
|---|---|
dirichlet(<alpha=> |
Dirichlet distribution with parameter vector |
iwish(<df=> |
Inverse Wishart distribution with |
mvn(<mu=> |
Multivariate normal distribution with mean vector |
multinom(<p=> |
Multinomial distribution with probability vector |
 , <b=>
, <b=>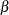 )
) 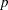 )
)  , <prob|p=>
, <prob|p=> 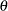 , <scale|s=>
, <scale|s=>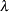 )
)  )
)  distribution with
distribution with  . You can use the alias echisq for this distribution.
. You can use the alias echisq for this distribution.  . You can use the alias eexpon for this distribution.
. You can use the alias eexpon for this distribution.  and scale or inverse-scale
and scale or inverse-scale  . You can use the alias egamma for this distribution.
. You can use the alias egamma for this distribution.  . You can use the alias eichisq for this distribution.
. You can use the alias eichisq for this distribution.  . You can use the alias eigamma for this distribution.
. You can use the alias eigamma for this distribution.  )
)  . You can use the alias esichisq for this distribution.
. You can use the alias esichisq for this distribution.  )
) 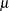 , sd=
, sd=  distribution with mean
distribution with mean  )
)  , and scale parameter
, and scale parameter  .
.  )
) 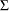 )
)