The GLMSELECT Procedure

Traditional implementations of FORWARD and STEPWISE selection methods start by computing the augmented crossproduct matrix for all the specified effects. This initial crossproduct matrix is updated as effects enter or leave the current model by sweeping the columns corresponding to the parameters of the entering or departing effects. Building the starting crossproduct matrix can be done with a single pass through the data and requires 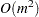storage and 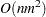work, where is the number of observations and is the number of parameters. If 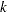selection steps are done, then the total work sweeping effects in and out of the model is 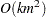. When 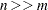, the work required is dominated by the time spent forming the crossproduct matrix. However, when is large (tens of thousands), just storing the crossproduct matrix becomes intractable even though the number of selected parameters might be small. Note also that when interactions of classification effects are considered, the number of parameters considered can be large, even though the number of effects considered is much smaller.

When the number of selected parameters is smaller than the total number of parameters, it turns out that many of the crossproducts are not needed in the selection process. Let 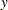denote the dependent variable, and suppose at some step of the selection process that 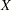denotes the 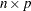design matrix columns corresponding to the currently selected model. Let 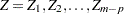denote the design matrix columns corresponding to the 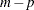effects not yet in the model. Then in order to compute the reduction in the residual sum of squares when 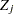is added to the model, the only additional crossproducts needed are 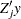, , 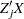and 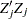. Note that it is not necessary to compute any of 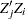with 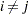and if 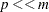, and this yields a substantial saving in both memory required and computational work. Note, however, that this strategy does require a pass through the data at any step where adding an effect to the model is considered.

PROC GLMSELECT supports both of these strategies for building the crossproduct matrix. You can choose which of these strategies to use by specifying the BUILDSSCP=FULL or BUILDSSCP=INCREMENTAL option in the PERFORMANCE statement. If you request BACKWARD selection, then the full SSCP matrix is required. Similarly, if you request the BIC or CP criterion as the SELECT=, CHOOSE=, or STOP= criterion, or if you request the display of one or both of these criteria with the STATS=BIC, STATS=CP, or STATS=ALL option, then the full model needs to be computed. If you do not specify the BUILDSSCP= option, then PROC GLMSELECT switches to the incremental strategy if the number of effects is greater than one hundred. This default strategy is designed to give good performance when the number of selected parameters is less than about 20% of the total number of parameters. Hence if you choose options that you know will cause the selected model to contain a significantly higher percentage of the total number of candidate parameters, then you should consider specifying BUILDSSCP=FULL. Conversely, if you specify fewer than 100 effects in the MODEL statement but many of these effects have a large number of associated parameters, then specifying BUILDSSCP=INCREMENTAL might result in improved performance.