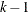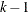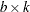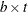FOCUS AREAS
Contents | SAS Program | PDF

The %MktBIBD Macro

Introduction

The %MktBIBD autocall macro finds balanced incomplete block designs (BIBDs). A BIBD is a list of treatments that appear together in blocks. Each block contains a subset of the treatments. BIBDs can be used in marketing research to construct partial-profile designs. The entries in the BIBD indicate which attributes are to be shown in each set. 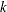For example, a BIBD could be used when there are $t$ attributes or messages (treatments) and $k$ are shown at a time. A total of 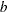$b$ sets of attributes (blocks) are shown. BIBDs are also used in marketing research to construct MaxDiff (best-worst) designs. In a MaxDiff study, subjects are shown sets (blocks) of messages or product attributes (treatments) and are asked to choose the best (or most important) from each set along with the worst (or least important).

Note: The version of the %MktBIBD macro that is documented here requires SAS 9.01 or any subsequent release. An enhanced version of the %MktBIBD macro is included in the SAS 940m3 maintenance release. The enhanced version requires SAS 940m1 or any subsequent release. The documentation for the enhanced version of the macro is published at http://support.sas.com/rnd/app/macros/MktBIBD/mktbibd.htm.

BIBD Parameters

The parameters of a BIBD are as follows:

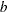  • $b$ specifies the number of blocks. In a partial-profile design, this is the number of profiles. In a MaxDiff design, this is the number of sets.

  • $t$ specifies the number of treatments. In a partial-profile or MaxDiff design, this is the total number of attributes or messages.

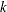  • $k$ specifies the block size, which is the number of treatments in each block. In a partial-profile or MaxDiff design, this is the number of attributes or messages that are shown at one time.

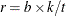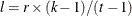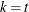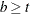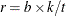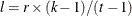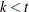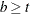If $r = b \times k / t$ and $l = r \times (k - 1) / (t - 1)$ are integers, and $k = t$ and $b \ge t$, then a complete block design might be possible. This is a necessary but not sufficient condition for the existence of a complete block design. If $r = b \times k / t$ and $l = r \times (k - 1) / (t - 1)$ are integers, and $k < t$ and $b \ge t$, then a balanced incomplete block design might be possible. This is a necessary but not sufficient condition for the existence of a BIBD. You can use the macro %MktBSize to find parameters in which BIBDs might exist. The %MktBIBD macro uses PROC OPTEX and a computerized search to find BIBDs. It does not have a library of BIBDs or use combinatorial constructions. Hence, it does not always find a BIBD even when one is known to exist. However, it usually works quite well in finding small BIBDs or something close for larger problems.

%MktBIBD Macro Syntax

%MktBIBD(B=b, K=k, T=t <, optional arguments>)

Required Arguments

B=b
NSETS=b

specifies the number of blocks. In a partial-profile design, this is the number of profiles. In a MaxDiff design, this is the number of sets.

K=k
SETSIZE=k

specifies the block size, which is the number of treatments in each block. In a partial-profile or MaxDiff design, this is the number of attributes or messages that are shown at one time in each set.

T=t
NATTRS=t

specifies the number of treatments. In a partial-profile or MaxDiff design, this is the total number of attributes or messages. When the NATTRS= option is specified, the output uses the word "Attribute" rather than "Treatment" and the word "Set" rather than "Block."

Optional Arguments

GROUP=n

specifies the number of groups into which the design is to be divided. This could be useful with MaxDiff and partial profiles. By default, the design is not divided into groups.

OPTIONS=NEIGHBOR | SERIAL | POSITION

specifies binary options. You can specify the following:

NEIGHBOR

optimizes nondirectional row-neighbor balance and also position. The goal is for pairs of treatments, which are constructed from each of the first $k-1$ treatments in each block along with the treatment that follows it, to occur equally often in the design. The order of the treatments within each pair does not matter in evaluating row-neighbor balance. That is, treatment 1 appearing before treatment 2 is counted the same as treatment 2 appearing before treatment 1.

SERIAL

optimizes directional row-neighbor balance and also position. The goal is for pairs of treatments, which are constructed from each of the first $k - 1$ treatments in each block along with the treatment that follows it, to occur equally often in the design. In contrast to OPTIONS=NEIGHBOR, treatment 2 appearing before treatment 1 is counted as different from treatment 1 appearing before treatment 2.

POSITION

optimizes position frequencies. The goal is for each treatment to appear equally often in each position.

By default, OPTIONS=POSITION.

OPTITER=n1 <n2 <n3>>

specifies the number of PROC OPTEX iterations. If one number is specified, it is just the number of iterations. If two numbers, n1 and n2, are specified, n1 iterations are performed and then efficiency is checked. If the block design efficiency criterion is 100, the iterations stop. Otherwise, this process is repeated up to n2 times for a maximum of n1 $\times $ n2 iterations. The default for n2, when it is missing, is 1,000 when the parameters conform to the necessary conditions for a BIBD and 5 otherwise. The third value is the maximum amount of time (in minutes) to spend in PROC OPTEX. The default for the time value, when it is missing, is 5 minutes when the parameters conform to the necessary conditions for a BIBD and 0.5 minutes otherwise. Hence, when the parameters conform to the necessary conditions for a BIBD, the default is OPTITER=500 1000 5; otherwise, the default is OPTITER=500 5 0.5. For larger problems, you might want to specify values smaller than the defaults.

OUT=SAS-data-set

specifies the output data set name for the $b \times k$ BIBD (or more generally, the incomplete block design). By default, OUT=BIBD.

OUTF=SAS-data-set

specifies the output data set name for the $bk \times 2$ factorial design matrix. By default, OUTF=Factorial.

OUTI=SAS-data-set

specifies the output data set name for the $b \times t$ incidence matrix. By default, is OUTI=Incidence.

OUTS=SAS-data-set

specifies the output data set name for the $b \times k$ sorted design. By default, OUTS=Sorted.

POSITER=n1 <n2 <n3>>

specifies the number of iterations for the algorithm that attempts to optimize the treatment by position frequencies. By default, POSITER=200 5000 2. The first value specifies the number of times to try to refine the design. The second value specifies the number of times to start from scratch with a different random start. Larger values increase the chances of finding better treatment by position frequencies at a cost of slower run times. The third value is the maximum amount of time (in minutes) to spend optimizing the positional frequencies. Specify POSITER= or POSITER=0 to request a design without optimizing position.

SEED=n

specifies the random number seed. By default, SEED=0, and clock time is used to make the random number seed. If you specify a random number seed, results should be reproducible within a SAS release for a particular operating system and for a particular version of the macro. However, because of machine and macro differences, some results might not be exactly reproducible everywhere, although you would expect the efficiency differences to be slight.

WEIGHTS=n1 n2

specifies weights for position balance and row-neighbor balance. Specify two nonnegative numeric values. The total badness is a weighted sum of the position badness and the row-neighbor badness. By default, WEIGHTS=1 2, so by default, row-neighbor balance is given the most weight. You can specify a weight of 0, for example, for the position balance (the first value) to optimize only row-neighbor balance.

Help Argument

You can specify either of the following to display the option names and simple examples of the macro syntax: 

%mktbibd(help)
%mktbibd(?)

%MktBIBD Macro Notes

This macro specifies options nonotes throughout most of its execution. If you want to see all the notes, submit the following statement before running the macro: 

%let mktopts = notes;

To see the macro version, submit the following statement before running the macro: 

%let mktopts = version;

Example 1: Balanced Incomplete Block Design

The following invocation of the %MktBIBD macro generates a BIBD design that contains 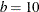$b=10$ blocks, 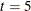$t=5$ treatments, and 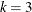$k=3$ treatments per block: 

%mktbibd(b=10, t=5, k=3, seed=104)

Figure 1 displays the design information. The block design efficiency of 100 indicates that the %MktBIBD macro found a BIBD. In many cases, it finds a design that is close to a BIBD, but each of the pairwise frequencies is not constant. For many marketing research problems, this is good enough.

Figure 1: BIBD Description

Block Design Efficiency Criterion 100.0000

Number of Treatments, t 5

Block Size, k 3

Number of Blocks, b 10

Treatment Frequency 6

Pairwise Frequency 3

Total Sample Size 30

Positional Frequencies Optimized? Yes 



 
Figure 2 shows the treatment by treatment frequencies. Each of the 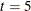$t=5$ treatments occurs exactly six times in the design, and each treatment occurs together with every other treatment three times. 
  
Figure 2: Treatment by Treatment Frequencies









Treatment by Treatment Frequencies

















 
1
2
3
4
5

1
6
3
3
3
3

2
.
6
3
3
3

3
.
.
6
3
3

4
.
.
.
6
3

5
.
.
.
.
6










 
When the %MktBIBD macro makes a BIBD, it tries to optimize the treatment by position frequencies. In other words, it tries to ensure that each treatment occurs in each of the 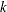$k$ positions equally often, or at least close to equally often. Figure 3 shows the treatment by position frequencies, which are perfect for this design. 
  
Figure 3: Treatment by Position Frequencies









Treatment by Position Frequencies

















 
1
2
3

1
2
2
2

2
2
2
2

3
2
2
2

4
2
2
2

5
2
2
2










 
Figure 4 shows the design. 
  
Figure 4: Balanced Incomplete Block Design





Balanced Incomplete Block Design






x1
x2
x3

3
5
2

1
5
2

3
2
4

4
3
1

5
3
1

1
2
3

4
1
5

5
4
3

2
1
4

2
4
5










 
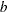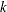Every BIBD also has a binary representation, or incidence matrix, with $b$ rows and $t$ columns and $k$ ones that indicate which treatments appear in each block. The %MktBIBD macro saves the incidence matrix in the OUTI= data set (which is named Incidence by default). The following statements display the incidence matrix: 
proc print data=incidence noobs;
run;

Figure 5 displays the results. 
  
Figure 5: Incidence Matrix









b1
b2
b3
b4
b5

0
1
1
0
1

1
1
0
0
1

0
1
1
1
0

1
0
1
1
0

1
0
1
0
1

1
1
1
0
0

1
0
0
1
1

0
0
1
1
1

1
1
0
1
0

0
1
0
1
1










 
You can also view the BIBD arrayed as a block by treatment factorial design. By default, the %MktBIBD macro saves the 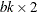$bk \times 2$ design matrix in a data set named Factorial. The following statements display the first 9 (out of 30) observations: 
proc print data=factorial(obs=9) noobs;
run;

Figure 6 displays the results. 
  
Figure 6: BIBD as a Block by Treatment Factorial Design









Block
Treatment

1
3

1
5

1
2

2
1

2
5

2
2

3
3

3
2

3
4










 
Example 2: BIBD with Directional and Nondirectional Row-Neighbor Balance
The following invocation of the %MktBIBD macro generates a BIBD that has nondirectional row-neighbor balance: 
%mktbibd(b=14, t=7, k=4, options=neighbor, seed=104)

Figure 7 displays the results. 
  
Figure 7: BIBD with Nondirectional Row-Neighbor Balance









Block Design Efficiency Criterion
100.0000

















Number of Treatments, t
7

















Block Size, k
4

















Number of Blocks, b
14

















Treatment Frequency
8

















Pairwise Frequency
4

















Total Sample Size
56

















Positional Frequencies Optimized?
Yes

















Row-Neighbor Frequencies Optimized?
Yes

















Treatment by Treatment Frequencies

















 
1
2
3
4
5
6
7

1
8
4
4
4
4
4
4

2
.
8
4
4
4
4
4

3
.
.
8
4
4
4
4

4
.
.
.
8
4
4
4

5
.
.
.
.
8
4
4

6
.
.
.
.
.
8
4

7
.
.
.
.
.
.
8

















Treatment by Position Frequencies

















 
1
2
3
4

1
2
2
2
2

2
2
2
2
2

3
2
2
2
2

4
2
2
2
2

5
2
2
2
2

6
2
2
2
2

7
2
2
2
2

















Row-Neighbor Frequencies

















 
1
2
3
4
5
6
7

1
.
2
2
2
2
2
2

2
.
.
2
2
2
2
2

3
.
.
.
2
2
2
2

4
.
.
.
.
2
2
2

5
.
.
.
.
.
2
2

6
.
.
.
.
.
.
2

7
.
.
.
.
.
.
.













Balanced Incomplete Block Design






x1
x2
x3
x4

3
4
2
5

5
6
1
4

1
4
5
3

7
1
6
4

4
5
7
2

5
3
7
6

3
7
5
1

1
2
4
7

6
2
1
5

4
7
6
3

2
3
4
6

2
6
3
1

6
5
2
7

7
1
3
2










 
The resulting design is a BIBD, where each of the seven treatments appears in each of the four positions within a block exactly twice. Furthermore, the row-neighbor frequencies show that each of the 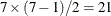$7 \times (7 - 1) / 2 = 21$ pairs of treatments occurs exactly twice. The pairs in this design are 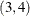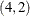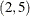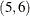$(3,4)$, $(4,2)$, $(2,5)$, $(5,6)$, and so on. The order of the treatments in each pair is ignored. Hence, in this design, with the nondirectional row-neighbor balance, the 2 followed by 5 in the first row of the design is treated the same as the 5 followed by 2 in the second-last row of the design. Usually this design is easily found in a few seconds. The last line of the first table ("Row-Neighbor Frequencies Optimized? Yes") along with the constant row-neighbor frequencies shows that perfect row-neighbor balance was achieved. 
The following finds a BIBD that has row-neighbor balance, where the order of the treatments does matter, by specifying OPTIONS=SERIAL: 
%mktbibd(b=14, t=7, k=4, options=serial, seed=361699)

Figure 8 displays the results. 
  
Figure 8: BIBD with Directional Row-Neighbor Balance









Block Design Efficiency Criterion
100.0000

















Number of Treatments, t
7

















Block Size, k
4

















Number of Blocks, b
14

















Treatment Frequency
8

















Pairwise Frequency
4

















Total Sample Size
56

















Positional Frequencies Optimized?
Yes

















Row-Neighbor Frequencies Optimized?
Yes

















Treatment by Treatment Frequencies

















 
1
2
3
4
5
6
7

1
8
4
4
4
4
4
4

2
.
8
4
4
4
4
4

3
.
.
8
4
4
4
4

4
.
.
.
8
4
4
4

5
.
.
.
.
8
4
4

6
.
.
.
.
.
8
4

7
.
.
.
.
.
.
8

















Treatment by Position Frequencies

















 
1
2
3
4

1
2
2
2
2

2
2
2
2
2

3
2
2
2
2

4
2
2
2
2

5
2
2
2
2

6
2
2
2
2

7
2
2
2
2

















Row-Neighbor Frequencies

















 
1
2
3
4
5
6
7

1
.
1
1
1
1
1
1

2
1
.
1
1
1
1
1

3
1
1
.
1
1
1
1

4
1
1
1
.
1
1
1

5
1
1
1
1
.
1
1

6
1
1
1
1
1
.
1

7
1
1
1
1
1
1
.













Balanced Incomplete Block Design






x1
x2
x3
x4

1
4
2
5

3
1
5
7

4
5
1
7

2
3
7
1

6
7
5
3

7
6
4
1

7
2
6
5

1
3
4
6

3
5
2
4

4
7
3
2

5
4
3
6

5
6
1
2

6
2
7
4

2
1
6
3










 
When OPTIONS=SERIAL, the row-neighbor frequencies appear both above and below the diagonal. Each pair of treatments occurs exactly once. In this design, which has the serial (directional) row-neighbor balance, the 2 followed by 5 in the first row of the design is not treated the same as the 5 followed by 2 in the ninth row of the design. 
An OPTIONS=SERIAL design is usually much harder to find than an OPTIONS=NEIGHBOR design. In this example, a random number seed that is known to produce an optimal design quickly was chosen. You usually have to run the macro more than once or change some options (such as the time value in the POSITER= option) and iterate for up to a few hours to find an equivalent design. 
The following invocation of the %MktBIBD macro requests the same design but specifies a different pseudorandom number seed: 
%mktbibd(b=14, t=7, k=4, options=serial, seed=104)

Figure 9 displays the results. 
  
Figure 9: BIBD with Directional Row-Neighbor Balance









Block Design Efficiency Criterion
100.0000

















Number of Treatments, t
7

















Block Size, k
4

















Number of Blocks, b
14

















Treatment Frequency
8

















Pairwise Frequency
4

















Total Sample Size
56

















Positional Frequencies Optimized?
No

















Row-Neighbor Frequencies Optimized?
No

















Treatment by Treatment Frequencies

















 
1
2
3
4
5
6
7

1
8
4
4
4
4
4
4

2
.
8
4
4
4
4
4

3
.
.
8
4
4
4
4

4
.
.
.
8
4
4
4

5
.
.
.
.
8
4
4

6
.
.
.
.
.
8
4

7
.
.
.
.
.
.
8

















Treatment by Position Frequencies

















 
1
2
3
4

1
2
2
2
2

2
2
3
2
1

3
2
2
2
2

4
2
2
2
2

5
2
2
2
2

6
2
2
2
2

7
2
1
2
3

















Row-Neighbor Frequencies

















 
1
2
3
4
5
6
7

1
.
1
1
1
1
1
1

2
1
.
1
1
1
2
1

3
1
1
.
1
1
1
1

4
1
1
1
.
1
1
1

5
1
1
1
1
.
1
1

6
1
1
1
1
1
.
1

7
1
1
1
1
1
0
.













Balanced Incomplete Block Design






x1
x2
x3
x4

2
6
1
4

5
4
3
1

1
5
7
2

7
3
5
6

7
5
2
4

2
3
4
6

1
2
6
5

5
1
6
3

4
2
5
3

6
7
4
5

3
6
2
7

3
2
1
7

6
4
7
1

4
1
3
7










 
The following requests a design where it is not possible to have constant frequencies in the row-neighbor frequencies matrix: 
%mktbibd(b=7, t=7, k=4, options=serial, seed=104)

Figure 10 displays the results. 
  
Figure 10: BIBD with Unachievable Directional Row-Neighbor Balance









Block Design Efficiency Criterion
100.0000

















Number of Treatments, t
7

















Block Size, k
4

















Number of Blocks, b
7

















Treatment Frequency
4

















Pairwise Frequency
2

















Total Sample Size
28

















Positional Frequencies Optimized?
Yes

















Row-Neighbor Frequencies Optimized?
Yes

















Treatment by Treatment Frequencies

















 
1
2
3
4
5
6
7

1
4
2
2
2
2
2
2

2
.
4
2
2
2
2
2

3
.
.
4
2
2
2
2

4
.
.
.
4
2
2
2

5
.
.
.
.
4
2
2

6
.
.
.
.
.
4
2

7
.
.
.
.
.
.
4

















Treatment by Position Frequencies

















 
1
2
3
4

1
1
1
1
1

2
1
1
1
1

3
1
1
1
1

4
1
1
1
1

5
1
1
1
1

6
1
1
1
1

7
1
1
1
1

















Row-Neighbor Frequencies

















 
1
2
3
4
5
6
7

1
.
0
1
1
1
0
0

2
0
.
1
0
0
1
1

3
1
0
.
0
0
1
1

4
0
1
0
.
1
1
0

5
1
1
0
0
.
0
1

6
0
0
1
1
1
.
0

7
1
1
0
1
0
0
.













Balanced Incomplete Block Design






x1
x2
x3
x4

6
4
2
7

7
1
3
6

5
2
6
3

4
6
5
1

3
7
4
5

2
3
1
4

1
5
7
2










 
The %MktBIBD macro reports that the row-neighbor frequencies are optimized because a mix of zeros and ones with no twos or larger values is optimal for this specification. However, the nonconstant frequencies indicate that row-neighbor balance is not possible for this BIBD.