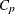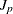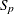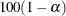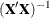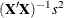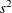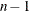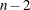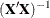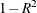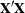The REG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics
Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics -
Examples

- References
MODEL Statement
-
<label:> MODEL dependents = <regressors> </ options>;
After the keyword MODEL, the dependent (response) variables are specified, followed by an equal sign and the regressor variables.
Variables specified in the MODEL
statement must be numeric variables in the data set being analyzed. For example, if you want to specify a quadratic term
for variable X1 in the model, you cannot use X1*X1 in the MODEL
statement but must create a new variable (for example, X1SQUARE=X1*X1) in a DATA step and use this new variable in the MODEL
statement. The label in the MODEL
statement is optional.
Table 97.5 summarizes the options available in the MODEL statement. Equations for the statistics available are given in the section Model Fit and Diagnostic Statistics.
Table 97.5: MODEL Statement Options
|
Option |
Description |
|---|---|
|
Model Selection and Details of Selection |
|
|
Specifies model selection method |
|
|
Specifies maximum number of subset models displayed or output to the OUTEST= data set |
|
|
Produces summary statistics at each step |
|
|
Specifies the display details for FORWARD, BACKWARD, and STEPWISE methods |
|
|
Provides names for groups of variables |
|
|
Includes first n variables in the model |
|
|
Specifies maximum number of steps that might be performed |
|
|
Fits a model without the intercept term |
|
|
Performs incomplete principal component analysis and outputs estimates to the OUTEST= data set |
|
|
Performs ridge regression analysis and outputs estimates to the OUTEST= data set |
|
|
Sets criterion for entry into model |
|
|
Sets criterion for staying in model |
|
|
Specifies number of variables in model to begin the comparing and switching process |
|
|
Stops selection criterion |
|
|
Statistics |
|
|
Computes adjusted R square |
|
|
Computes Akaike’s information criterion |
|
|
Computes parameter estimates for each model |
|
|
Computes Sawa’s Bayesian information criterion |
|
|
Computes Mallows’ |
|
|
Computes estimated MSE of prediction assuming multivariate normality |
|
|
Computes |
|
|
Computes MSE for each model |
|
|
Computes Amemiya’s prediction criterion |
|
|
Displays root MSE for each model |
|
|
Computes the SBC statistic |
|
|
Computes |
|
|
Computes error sum of squares for each model |
|
|
Data Set Options |
|
|
Outputs the number of regressors, the error degrees of freedom, and the model R square to the OUTEST= data set |
|
|
Outputs standard errors of the parameter estimates to the OUTEST= data set |
|
|
Outputs standardized parameter estimates to the OUTEST= data set. Use only with the RIDGE= or PCOMIT= option. |
|
|
Outputs the variance inflation factors to the OUTEST= data set. Use only with the RIDGE= or PCOMIT= option. |
|
|
Outputs the PRESS statistic to the OUTEST= data set |
|
|
Has same effect as the EDF option |
|
|
Regression Calculations |
|
|
Displays inverse of sums of squares and crossproducts |
|
|
Displays sums-of-squares and crossproducts matrix |
|
|
Details on Estimates |
|
|
Displays heteroscedasticity- consistent covariance matrix of estimates and heteroscedasticity-consistent standard errors |
|
|
Specifies method for computing the asymptotic heteroscedasticity-consistent covariance matrix |
|
|
Produces collinearity analysis |
|
|
Produces collinearity analysis with intercept adjusted out |
|
|
Displays correlation matrix of estimates |
|
|
Displays covariance matrix of estimates |
|
|
Displays heteroscedasticity-consistent standard errors |
|
|
Specifies method for computing the asymptotic heteroscedasticity-consistent covariance matrix |
|
|
Performs lack-of-fit test |
|
|
Displays squared semipartial correlation coefficients computed using Type I sums of squares |
|
|
Displays squared partial correlation coefficients computed using Type I sums of squares |
|
|
Displays squared partial correlation coefficients computed using Type II sums of squares |
|
|
Displays squared semipartial correlation coefficients computed using Type I sums of squares |
|
|
Displays squared semipartial correlation coefficients computed using Type II sums of squares |
|
|
Displays a sequence of parameter estimates during selection process |
|
|
Tests that first and second moments of model are correctly specified |
|
|
Displays the studentized residuals by using a series of asterisks |
|
|
Displays the sequential sums of squares |
|
|
Displays the partial sums of squares |
|
|
Displays standardized parameter estimates |
|
|
Displays tolerance values for parameter estimates |
|
|
Displays heteroscedasticity-consistent standard errors |
|
|
Computes variance-inflation factors |
|
|
Predicted and Residual Values |
|
|
Computes |
|
|
Computes |
|
|
Computes |
|
|
Computes a Durbin-Watson statistic |
|
|
Computes a Durbin-Watson statistic and p-value |
|
|
Computes influence statistics |
|
|
Computes predicted values |
|
|
Displays partial regression plots for each regressor |
|
|
Displays partial regression data |
|
|
Produces analysis of residuals |
|
|
Display Options and Other Options |
|
|
Requests the following options: |
|
|
Sets significance value for confidence and prediction intervals and tests |
|
|
Suppresses display of results |
|
|
Specifies the true standard deviation of error term for computing CP and BIC |
|
|
Sets criterion for checking for singularity |
|
You can specify the following options in the MODEL statement after a slash (/).