The REG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics
Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics -
Examples

- References
Output Data Sets
OUTEST= Data Set
The OUTEST= specification produces a TYPE=EST output SAS data set containing estimates and optional statistics from the regression models. For each BY group on each dependent variable occurring in each MODEL statement, PROC REG outputs an observation to the OUTEST= data set. The variables output to the data set are as follows:
-
the BY variables, if any
-
_MODEL_, a character variable containing the label of the corresponding MODEL statement, or MODELn if no label is specified, where n is 1 for the first MODEL statement, 2 for the second model statement, and so on -
_TYPE_, a character variable with the value ’PARMS’ for every observation -
_DEPVAR_, the name of the dependent variable -
_RMSE_, the root mean squared error or the estimate of the standard deviation of the error term -
Intercept, the estimated intercept, unless the NOINT option is specified -
all the variables listed in any MODEL or VAR statement. Values of these variables are the estimated regression coefficients for the model. A variable that does not appear in the model corresponding to a given observation has a missing value in that observation. The dependent variable in each model is given a value of –1.
If you specify the COVOUT option, the covariance matrix of the estimates is output after the estimates; the _TYPE_ variable is set to the value ’COV’ and the names of the rows are identified by the character variable, _NAME_.
If you specify the TABLEOUT option, the following statistics listed by _TYPE_ are added after the estimates:
-
STDERR, the standard error of the estimate
-
T, the t statistic for testing if the estimate is zero
-
PVALUE, the associated p-value
-
LnB, the
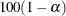 lower confidence limit for the estimate, where n is the nearest integer to
lower confidence limit for the estimate, where n is the nearest integer to 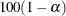 and
and  defaults to 0.05 or is set by using the ALPHA= option in the PROC REG
or MODEL
statement
defaults to 0.05 or is set by using the ALPHA= option in the PROC REG
or MODEL
statement
-
UnB, the
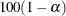 upper confidence limit for the estimate
upper confidence limit for the estimate
Specifying the option ADJRSQ, AIC, BIC, CP, EDF, GMSEP, JP, MSE, PC, RSQUARE, SBC, SP, or SSE in the PROC REG
or MODEL
statement automatically outputs these statistics and the model  for each model selected, regardless of the model selection method. Additional variables, in order of occurrence, are as follows:
for each model selected, regardless of the model selection method. Additional variables, in order of occurrence, are as follows:
-
_IN_, the number of regressors in the model not including the intercept -
_P_, the number of parameters in the model including the intercept, if any -
_EDF_, the error degrees of freedom -
_SSE_, the error sum of squares, if the SSE option is specified -
_MSE_, the mean squared error, if the MSE option is specified -
_RSQ_, the R square statistic -
_ADJRSQ_, the adjusted R square, if the ADJRSQ option is specified -
_CP_, the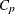 statistic, if the CP option is specified
statistic, if the CP option is specified
-
_SP_, the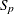 statistic, if the SP option is specified
statistic, if the SP option is specified
-
_JP_, the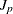 statistic, if the JP option is specified
statistic, if the JP option is specified
-
_PC_, the PC statistic, if the PC option is specified -
_GMSEP_, the GMSEP statistic, if the GMSEP option is specified -
_AIC_, the AIC statistic, if the AIC option is specified -
_BIC_, the BIC statistic, if the BIC option is specified -
_SBC_, the SBC statistic, if the SBC option is specified
The following statements produce and display the OUTEST= data set. This example uses the population data given in the section Polynomial Regression. Figure 97.19 through Figure 97.21 show the regression equations and the resulting OUTEST= data set.
proc reg data=USPopulation outest=est; m1: model Population=Year; m2: model Population=Year YearSq; run; proc print data=est; run;
Figure 97.19: Regression Output for Model M1
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 1 | 146869 | 146869 | 228.92 | <.0001 |
| Error | 20 | 12832 | 641.58160 | ||
| Corrected Total | 21 | 159700 | |||
| Root MSE | 25.32946 | R-Square | 0.9197 |
|---|---|---|---|
| Dependent Mean | 94.64800 | Adj R-Sq | 0.9156 |
| Coeff Var | 26.76175 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | -2345.85498 | 161.39279 | -14.54 | <.0001 |
| Year | 1 | 1.28786 | 0.08512 | 15.13 | <.0001 |
Figure 97.20: Regression Output for Model M2
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 2 | 159529 | 79765 | 8864.19 | <.0001 |
| Error | 19 | 170.97193 | 8.99852 | ||
| Corrected Total | 21 | 159700 | |||
| Root MSE | 2.99975 | R-Square | 0.9989 |
|---|---|---|---|
| Dependent Mean | 94.64800 | Adj R-Sq | 0.9988 |
| Coeff Var | 3.16938 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | 21631 | 639.50181 | 33.82 | <.0001 |
| Year | 1 | -24.04581 | 0.67547 | -35.60 | <.0001 |
| YearSq | 1 | 0.00668 | 0.00017820 | 37.51 | <.0001 |
Figure 97.21: OUTEST= Data Set
The following modification of the previous example uses the TABLEOUT and ALPHA= options to obtain additional information in the OUTEST= data set:
proc reg data=USPopulation outest=est tableout alpha=0.1; m1: model Population=Year/noprint; m2: model Population=Year YearSq/noprint; run; proc print data=est; run;
Notice that the TABLEOUT option causes standard errors, t statistics, p-values, and confidence limits for the estimates to be added to the OUTEST= data set. Also note that the ALPHA= option is used to set the confidence level at 90%. The OUTEST= data set is shown in Figure 97.22.
Figure 97.22: The OUTEST= Data Set When TABLEOUT Is Specified
| Obs | _MODEL_ | _TYPE_ | _DEPVAR_ | _RMSE_ | Intercept | Year | Population | YearSq |
|---|---|---|---|---|---|---|---|---|
| 1 | m1 | PARMS | Population | 25.3295 | -2345.85 | 1.2879 | -1 | . |
| 2 | m1 | STDERR | Population | 25.3295 | 161.39 | 0.0851 | . | . |
| 3 | m1 | T | Population | 25.3295 | -14.54 | 15.1300 | . | . |
| 4 | m1 | PVALUE | Population | 25.3295 | 0.00 | 0.0000 | . | . |
| 5 | m1 | L90B | Population | 25.3295 | -2624.21 | 1.1411 | . | . |
| 6 | m1 | U90B | Population | 25.3295 | -2067.50 | 1.4347 | . | . |
| 7 | m2 | PARMS | Population | 2.9998 | 21630.89 | -24.0458 | -1 | 0.0067 |
| 8 | m2 | STDERR | Population | 2.9998 | 639.50 | 0.6755 | . | 0.0002 |
| 9 | m2 | T | Population | 2.9998 | 33.82 | -35.5988 | . | 37.5096 |
| 10 | m2 | PVALUE | Population | 2.9998 | 0.00 | 0.0000 | . | 0.0000 |
| 11 | m2 | L90B | Population | 2.9998 | 20525.11 | -25.2138 | . | 0.0064 |
| 12 | m2 | U90B | Population | 2.9998 | 22736.68 | -22.8778 | . | 0.0070 |
A slightly different OUTEST= data set is created when you use the RSQUARE selection method. The following statements request only the "best" model for each subset size but ask for a variety of model selection statistics, as well as the estimated regression coefficients. An OUTEST= data set is created and displayed. See Figure 97.23 and Figure 97.24 for the results.
proc reg data=fitness outest=est;
model Oxygen=Age Weight RunTime RunPulse RestPulse MaxPulse
/ selection=rsquare mse jp gmsep cp aic bic sbc b best=1;
run;
proc print data=est;
run;
Figure 97.23: PROC REG Output for Physical Fitness Data: Best Models
| Number in Model |
R-Square | C(p) | AIC | BIC | Estimated MSE of Prediction |
J(p) | MSE | SBC | Parameter Estimates | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intercept | Age | Weight | RunTime | RunPulse | RestPulse | MaxPulse | |||||||||
| 1 | 0.7434 | 13.6988 | 64.5341 | 65.4673 | 8.0546 | 8.0199 | 7.53384 | 67.40210 | 82.42177 | . | . | -3.31056 | . | . | . |
| 2 | 0.7642 | 12.3894 | 63.9050 | 64.8212 | 7.9478 | 7.8621 | 7.16842 | 68.20695 | 88.46229 | -0.15037 | . | -3.20395 | . | . | . |
| 3 | 0.8111 | 6.9596 | 59.0373 | 61.3127 | 6.8583 | 6.7253 | 5.95669 | 64.77326 | 111.71806 | -0.25640 | . | -2.82538 | -0.13091 | . | . |
| 4 | 0.8368 | 4.8800 | 56.4995 | 60.3996 | 6.3984 | 6.2053 | 5.34346 | 63.66941 | 98.14789 | -0.19773 | . | -2.76758 | -0.34811 | . | 0.27051 |
| 5 | 0.8480 | 5.1063 | 56.2986 | 61.5667 | 6.4565 | 6.1782 | 5.17634 | 64.90250 | 102.20428 | -0.21962 | -0.07230 | -2.68252 | -0.37340 | . | 0.30491 |
| 6 | 0.8487 | 7.0000 | 58.1616 | 64.0748 | 6.9870 | 6.5804 | 5.36825 | 68.19952 | 102.93448 | -0.22697 | -0.07418 | -2.62865 | -0.36963 | -0.02153 | 0.30322 |
Figure 97.24: PROC PRINT Output for Physical Fitness Data: OUTEST= Data Set
| Obs | _MODEL_ | _TYPE_ | _DEPVAR_ | _RMSE_ | Intercept | Age | Weight | RunTime | RunPulse | RestPulse | MaxPulse | Oxygen | _IN_ | _P_ | _EDF_ | _MSE_ | _RSQ_ | _CP_ | _JP_ | _GMSEP_ | _AIC_ | _BIC_ | _SBC_ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | MODEL1 | PARMS | Oxygen | 2.74478 | 82.422 | . | . | -3.31056 | . | . | . | -1 | 1 | 2 | 29 | 7.53384 | 0.74338 | 13.6988 | 8.01990 | 8.05462 | 64.5341 | 65.4673 | 67.4021 |
| 2 | MODEL1 | PARMS | Oxygen | 2.67739 | 88.462 | -0.15037 | . | -3.20395 | . | . | . | -1 | 2 | 3 | 28 | 7.16842 | 0.76425 | 12.3894 | 7.86214 | 7.94778 | 63.9050 | 64.8212 | 68.2069 |
| 3 | MODEL1 | PARMS | Oxygen | 2.44063 | 111.718 | -0.25640 | . | -2.82538 | -0.13091 | . | . | -1 | 3 | 4 | 27 | 5.95669 | 0.81109 | 6.9596 | 6.72530 | 6.85833 | 59.0373 | 61.3127 | 64.7733 |
| 4 | MODEL1 | PARMS | Oxygen | 2.31159 | 98.148 | -0.19773 | . | -2.76758 | -0.34811 | . | 0.27051 | -1 | 4 | 5 | 26 | 5.34346 | 0.83682 | 4.8800 | 6.20531 | 6.39837 | 56.4995 | 60.3996 | 63.6694 |
| 5 | MODEL1 | PARMS | Oxygen | 2.27516 | 102.204 | -0.21962 | -0.072302 | -2.68252 | -0.37340 | . | 0.30491 | -1 | 5 | 6 | 25 | 5.17634 | 0.84800 | 5.1063 | 6.17821 | 6.45651 | 56.2986 | 61.5667 | 64.9025 |
| 6 | MODEL1 | PARMS | Oxygen | 2.31695 | 102.934 | -0.22697 | -0.074177 | -2.62865 | -0.36963 | -0.021534 | 0.30322 | -1 | 6 | 7 | 24 | 5.36825 | 0.84867 | 7.0000 | 6.58043 | 6.98700 | 58.1616 | 64.0748 | 68.1995 |
OUTSSCP= Data Sets
The OUTSSCP= option produces a TYPE=SSCP output SAS data set containing sums of squares and crossproducts. A special row (observation)
and column (variable) of the matrix called Intercept contain the number of observations and sums. Observations are identified by the character variable _NAME_. The data set contains all variables used in MODEL
statements. You can specify additional variables that you want included in the crossproducts matrix with a VAR
statement.
The SSCP data set is used when a large number of observations are explored in many different runs. The SSCP data set can be saved and used for subsequent runs, which are much less expensive since PROC REG never reads the original data again. If you run PROC REG once to create only a SSCP data set, you should list all the variables that you might need in a VAR statement or include all the variables that you might need in a MODEL statement.
The following statements use the fitness data from Example 97.2 to produce an output data set with the OUTSSCP= option. The resulting output is shown in Figure 97.25.
proc reg data=fitness outsscp=sscp; var Oxygen RunTime Age Weight RestPulse RunPulse MaxPulse; run; proc print data=sscp; run;
Since a model is not fit to the data and since the only request is to create the SSCP data set, a MODEL statement is not required in this example. However, since the MODEL statement is not used, the VAR statement is required.
Figure 97.25: SSCP Data Set Created with OUTSSCP= Option: REG Procedure
| Obs | _TYPE_ | _NAME_ | Intercept | Oxygen | RunTime | Age | Weight | RestPulse | RunPulse | MaxPulse |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | SSCP | Intercept | 31.00 | 1468.65 | 328.17 | 1478.00 | 2400.78 | 1657.00 | 5259.00 | 5387.00 |
| 2 | SSCP | Oxygen | 1468.65 | 70429.86 | 15356.14 | 69767.75 | 113522.26 | 78015.41 | 248497.31 | 254866.75 |
| 3 | SSCP | RunTime | 328.17 | 15356.14 | 3531.80 | 15687.24 | 25464.71 | 17684.05 | 55806.29 | 57113.72 |
| 4 | SSCP | Age | 1478.00 | 69767.75 | 15687.24 | 71282.00 | 114158.90 | 78806.00 | 250194.00 | 256218.00 |
| 5 | SSCP | Weight | 2400.78 | 113522.26 | 25464.71 | 114158.90 | 188008.20 | 128409.28 | 407745.67 | 417764.62 |
| 6 | SSCP | RestPulse | 1657.00 | 78015.41 | 17684.05 | 78806.00 | 128409.28 | 90311.00 | 281928.00 | 288583.00 |
| 7 | SSCP | RunPulse | 5259.00 | 248497.31 | 55806.29 | 250194.00 | 407745.67 | 281928.00 | 895317.00 | 916499.00 |
| 8 | SSCP | MaxPulse | 5387.00 | 254866.75 | 57113.72 | 256218.00 | 417764.62 | 288583.00 | 916499.00 | 938641.00 |
| 9 | N | 31.00 | 31.00 | 31.00 | 31.00 | 31.00 | 31.00 | 31.00 | 31.00 |