The REG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics
Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics -
Examples

- References
Displayed Output
Many of the more specialized tables are described in detail in previous sections. Most of the formulas for the statistics are in Chapter 4: Introduction to Regression Procedures, while other formulas can be found in the section Model Fit and Diagnostic Statistics and the section Influence Statistics.
The analysis-of-variance table includes the following:
-
the Source of the variation, Model for the fitted regression, Error for the residual error, and C Total for the total variation after correcting for the mean. The Uncorrected Total Variation is produced when the NOINT option is used.
-
the degrees of freedom (DF) associated with the source
-
the Sum of Squares for the term
-
the Mean Square, the sum of squares divided by the degrees of freedom
-
the F Value for testing the hypothesis that all parameters are zero except for the intercept. This is formed by dividing the mean square for Model by the mean square for Error.
-
the Prob>F, the probability of getting a greater F statistic than that observed if the hypothesis is true. This is the significance probability.
Other statistics displayed include the following:
-
Root MSE is an estimate of the standard deviation of the error term. It is calculated as the square root of the mean square error.
-
Dep Mean is the sample mean of the dependent variable.
-
C.V. is the coefficient of variation, computed as 100 times Root MSE divided by Dep Mean. This expresses the variation in unitless values.
-
R-square is a measure between 0 and 1 that indicates the portion of the (corrected) total variation that is attributed to the fit rather than left to residual error. It is calculated as SS(Model) divided by SS(Total). It is also called the coefficient of determination. It is the square of the multiple correlation—in other words, the square of the correlation between the dependent variable and the predicted values.
-
Adj R-square, the adjusted R square, is a version of R square that has been adjusted for degrees of freedom. It is calculated as
![\[ \bar{R}^2 = 1 - \frac{(n-i)(1-R^2)}{n-p} \]](images/statug_reg0188.png)
where i is equal to 1 if there is an intercept and 0 otherwise, n is the number of observations used to fit the model, and p is the number of parameters in the model.
The parameter estimates and associated statistics are then displayed, and they include the following:
-
the Variable used as the regressor, including the name
Interceptto represent the estimate of the intercept parameter -
the degrees of freedom (DF) for the variable. There is one degree of freedom unless the model is not full rank.
-
the Parameter Estimate
-
the Standard Error, the estimate of the standard deviation of the parameter estimate
-
T for H0: Parameter=0, the t test that the parameter is zero. This is computed as the Parameter Estimate divided by the Standard Error.
-
the Prob > |T|, the probability that a t statistic would obtain a greater absolute value than that observed given that the true parameter is zero. This is the two-tailed significance probability.
If model-selection methods other than NONE, RSQUARE, ADJRSQ, and CP are used, the analysis-of-variance table and the parameter estimates with associated statistics are produced at each step. Also displayed are the following:
-
C(p), which is Mallows’
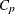 statistic
statistic
-
bounds on the condition number of the correlation matrix for the variables in the model (Berk 1977)
After statistics for the final model are produced, the following is displayed when the method chosen is FORWARD, BACKWARD, or STEPWISE:
-
a Summary table listing Step number, Variable Entered or Removed, Partial and Model R-square, and C(p) and F statistics
The RSQUARE method displays its results beginning with the model containing the fewest independent variables and producing
the largest R square. Results for other models with the same number of variables are then shown in order of decreasing R square,
and so on, for models with larger numbers of variables. The ADJRSQ and CP methods group models of all sizes together and display
results beginning with the model having the optimal value of adjusted R square and 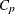 , respectively.
, respectively.
For each model considered, the RSQUARE, ADJRSQ, and CP methods display the following:
-
Number in Model or IN, the number of independent variables used in each model
-
R-square or RSQ, the squared multiple correlation coefficient
If the B option is specified, the RSQUARE, ADJRSQ, and CP methods produce the following:
-
Parameter Estimates, the estimated regression coefficients
If the B option is not specified, the RSQUARE, ADJRSQ, and CP methods display the following:
-
Variables in Model, the names of the independent variables included in the model