The REG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics
Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics -
Examples

- References
Testing for Lack of Fit
The test for lack of fit compares the variation around the model with "pure" variation within replicated observations. This
measures the adequacy of the specified model. In particular, if there are 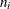 replicated observations
replicated observations  of the response all at the same values
of the response all at the same values 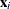 of the regressors, then you can predict the true response at
of the regressors, then you can predict the true response at 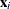 either by using the predicted value
either by using the predicted value 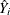 based on the model or by using the mean
based on the model or by using the mean 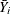 of the replicated values. The test for lack of fit decomposes the residual error into a component due to the variation of
the replications around their mean value (the "pure" error) and a component due to the variation of the mean values around
the model prediction (the "bias" error):
of the replicated values. The test for lack of fit decomposes the residual error into a component due to the variation of
the replications around their mean value (the "pure" error) and a component due to the variation of the mean values around
the model prediction (the "bias" error):
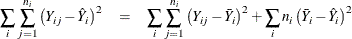
If the model is adequate, then both components estimate the nominal level of error; however, if the bias component of error is much larger than the pure error, then this constitutes evidence that there is significant lack of fit.
If some observations in your design are replicated, you can test for lack of fit by specifying the LACKFIT option in the MODEL statement (see Example 97.6). Note that, since all other tests use total error rather than pure error, you might want to hand-calculate the tests with respect to pure error if the lack of fit is significant. On the other hand, significant lack of fit indicates that the specified model is inadequate, so if this is a problem you can also try to refine the model.