The REG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics
Missing ValuesInput Data SetsOutput Data SetsInteractive AnalysisModel-Selection MethodsCriteria Used in Model-Selection MethodsLimitations in Model-Selection MethodsParameter Estimates and Associated StatisticsPredicted and Residual ValuesModels of Less Than Full RankCollinearity DiagnosticsModel Fit and Diagnostic StatisticsInfluence StatisticsReweighting Observations in an AnalysisTesting for HeteroscedasticityTesting for Lack of FitMultivariate TestsAutocorrelation in Time Series DataComputations for Ridge Regression and IPC AnalysisConstruction of Q-Q and P-P PlotsComputational MethodsComputer Resources in Regression AnalysisDisplayed OutputPlot Options Superseded by ODS GraphicsODS Table NamesODS Graphics -
Examples

- References
Input Data Sets
PROC REG does not compute new regressors. For example, if you want a quadratic term in your model, you should create a new variable when you prepare the input data. For example, the statement
model y=x1 x1*x1;
is not valid. Note that this MODEL statement is valid in the GLM procedure.
The input data set for most applications of PROC REG contains standard rectangular data, but special TYPE=CORR, TYPE=COV, and TYPE=SSCP data sets can also be used. TYPE=CORR and TYPE=COV data sets created by the CORR procedure contain means and standard deviations. In addition, TYPE=CORR data sets contain correlations and TYPE=COV data sets contain covariances. TYPE=SSCP data sets created in previous runs of PROC REG that used the OUTSSCP= option contain the sums of squares and crossproducts of the variables.
See Appendix A: Special SAS Data Sets, and the "SAS Files" section in SAS Language Reference: Concepts for more information about special SAS data sets.
These summary files save CPU time. It takes 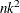 operations (where n = number of observations and k = number of variables) to calculate crossproducts; the regressions are of the order
operations (where n = number of observations and k = number of variables) to calculate crossproducts; the regressions are of the order 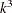 . When n is in the thousands and k is less than 10, you can save 99% of the CPU time by reusing the SSCP matrix rather than recomputing it.
. When n is in the thousands and k is less than 10, you can save 99% of the CPU time by reusing the SSCP matrix rather than recomputing it.
When you want to use a special SAS data set as input, PROC REG must determine the TYPE for the data set. PROC CORR and PROC REG automatically set the type for their output data sets. However, if you create the data set by some other means (such as a DATA step), you must specify its type with the TYPE= data set option. If the TYPE for the data set is not specified when the data set is created, you can specify TYPE= as a data set option in the DATA= option in the PROC REG statement. For example:
proc reg data=a(type=corr);
When a TYPE=CORR, TYPE=COV, or TYPE=SSCP data set is used with PROC REG, statements and options that require the original data values have no effect. The OUTPUT , PAINT , PLOT , and REWEIGHT statements and the MODEL and PRINT statement options P, R, CLM, CLI, DW, INFLUENCE, and PARTIAL are disabled since the original observations needed to calculate predicted and residual values are not present.
Example Using TYPE=CORR Data Set
The following statements use PROC CORR to produce an input data set for PROC REG. The fitness data for this analysis can be found in Example 97.2.
proc corr data=fitness outp=r noprint; var Oxygen RunTime Age Weight RunPulse MaxPulse RestPulse; run; proc print data=r; run; proc reg data=r; model Oxygen=RunTime Age Weight; run;
Since the OUTP= data set from PROC CORR is automatically set to TYPE=CORR, the TYPE= data set option is not required in this example. The data set containing the correlation matrix is displayed by the PRINT procedure as shown in Figure 97.15. Figure 97.16 shows results from the regression that uses the TYPE=CORR data as an input data set.
Figure 97.15: TYPE=CORR Data Set Created by PROC CORR
| Obs | _TYPE_ | _NAME_ | Oxygen | RunTime | Age | Weight | RunPulse | MaxPulse | RestPulse |
|---|---|---|---|---|---|---|---|---|---|
| 1 | MEAN | 47.3758 | 10.5861 | 47.6774 | 77.4445 | 169.645 | 173.774 | 53.4516 | |
| 2 | STD | 5.3272 | 1.3874 | 5.2114 | 8.3286 | 10.252 | 9.164 | 7.6194 | |
| 3 | N | 31.0000 | 31.0000 | 31.0000 | 31.0000 | 31.000 | 31.000 | 31.0000 | |
| 4 | CORR | Oxygen | 1.0000 | -0.8622 | -0.3046 | -0.1628 | -0.398 | -0.237 | -0.3994 |
| 5 | CORR | RunTime | -0.8622 | 1.0000 | 0.1887 | 0.1435 | 0.314 | 0.226 | 0.4504 |
| 6 | CORR | Age | -0.3046 | 0.1887 | 1.0000 | -0.2335 | -0.338 | -0.433 | -0.1641 |
| 7 | CORR | Weight | -0.1628 | 0.1435 | -0.2335 | 1.0000 | 0.182 | 0.249 | 0.0440 |
| 8 | CORR | RunPulse | -0.3980 | 0.3136 | -0.3379 | 0.1815 | 1.000 | 0.930 | 0.3525 |
| 9 | CORR | MaxPulse | -0.2367 | 0.2261 | -0.4329 | 0.2494 | 0.930 | 1.000 | 0.3051 |
| 10 | CORR | RestPulse | -0.3994 | 0.4504 | -0.1641 | 0.0440 | 0.352 | 0.305 | 1.0000 |
Figure 97.16: Regression on TYPE=CORR Data Set
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 3 | 656.27095 | 218.75698 | 30.27 | <.0001 |
| Error | 27 | 195.11060 | 7.22632 | ||
| Corrected Total | 30 | 851.38154 | |||
| Root MSE | 2.68818 | R-Square | 0.7708 |
|---|---|---|---|
| Dependent Mean | 47.37581 | Adj R-Sq | 0.7454 |
| Coeff Var | 5.67416 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | 93.12615 | 7.55916 | 12.32 | <.0001 |
| RunTime | 1 | -3.14039 | 0.36738 | -8.55 | <.0001 |
| Age | 1 | -0.17388 | 0.09955 | -1.75 | 0.0921 |
| Weight | 1 | -0.05444 | 0.06181 | -0.88 | 0.3862 |
The following example uses the saved crossproducts matrix:
proc reg data=fitness outsscp=sscp noprint; model Oxygen=RunTime Age Weight RunPulse MaxPulse RestPulse; run; proc print data=sscp; run; proc reg data=sscp; model Oxygen=RunTime Age Weight; run;
First, all variables are used to fit the data and create the SSCP data set. Figure 97.17 shows the PROC PRINT display of the SSCP data set. The SSCP data set is then used as the input data set for PROC REG, and a reduced model is fit to the data.
Figure 97.17: TYPE=SSCP Data Set Created by PROC REG
| Obs | _TYPE_ | _NAME_ | Intercept | RunTime | Age | Weight | RunPulse | MaxPulse | RestPulse | Oxygen |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | SSCP | Intercept | 31.00 | 328.17 | 1478.00 | 2400.78 | 5259.00 | 5387.00 | 1657.00 | 1468.65 |
| 2 | SSCP | RunTime | 328.17 | 3531.80 | 15687.24 | 25464.71 | 55806.29 | 57113.72 | 17684.05 | 15356.14 |
| 3 | SSCP | Age | 1478.00 | 15687.24 | 71282.00 | 114158.90 | 250194.00 | 256218.00 | 78806.00 | 69767.75 |
| 4 | SSCP | Weight | 2400.78 | 25464.71 | 114158.90 | 188008.20 | 407745.67 | 417764.62 | 128409.28 | 113522.26 |
| 5 | SSCP | RunPulse | 5259.00 | 55806.29 | 250194.00 | 407745.67 | 895317.00 | 916499.00 | 281928.00 | 248497.31 |
| 6 | SSCP | MaxPulse | 5387.00 | 57113.72 | 256218.00 | 417764.62 | 916499.00 | 938641.00 | 288583.00 | 254866.75 |
| 7 | SSCP | RestPulse | 1657.00 | 17684.05 | 78806.00 | 128409.28 | 281928.00 | 288583.00 | 90311.00 | 78015.41 |
| 8 | SSCP | Oxygen | 1468.65 | 15356.14 | 69767.75 | 113522.26 | 248497.31 | 254866.75 | 78015.41 | 70429.86 |
| 9 | N | 31.00 | 31.00 | 31.00 | 31.00 | 31.00 | 31.00 | 31.00 | 31.00 |
Figure 97.18 also shows the PROC REG results for the reduced model. (For the PROC REG results for the full model, see Figure 97.30.)
Figure 97.18: Regression on TYPE=SSCP Data Set
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares |
Mean Square |
F Value | Pr > F |
| Model | 3 | 656.27095 | 218.75698 | 30.27 | <.0001 |
| Error | 27 | 195.11060 | 7.22632 | ||
| Corrected Total | 30 | 851.38154 | |||
| Root MSE | 2.68818 | R-Square | 0.7708 |
|---|---|---|---|
| Dependent Mean | 47.37581 | Adj R-Sq | 0.7454 |
| Coeff Var | 5.67416 |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | 1 | 93.12615 | 7.55916 | 12.32 | <.0001 |
| RunTime | 1 | -3.14039 | 0.36738 | -8.55 | <.0001 |
| Age | 1 | -0.17388 | 0.09955 | -1.75 | 0.0921 |
| Weight | 1 | -0.05444 | 0.06181 | -0.88 | 0.3862 |
In the preceding example, the TYPE= data set option is not required since PROC REG sets the OUTSSCP= data set to TYPE=SSCP.