The NLMIXED Procedure

Logistic-Normal Model with Binomial Data

This example analyzes the data from Beitler and Landis (1985), which represent results from a multi-center clinical trial investigating the effectiveness of two topical cream treatments (active drug, control) in curing an infection. For each of eight clinics, the number of trials and favorable cures are recorded for each treatment. The SAS data set is as follows.

data infection;
   input clinic t x n;
   datalines;
1 1 11 36
1 0 10 37
2 1 16 20
2 0 22 32
3 1 14 19
3 0  7 19
4 1  2 16
4 0  1 17
5 1  6 17
5 0  0 12
6 1  1 11
6 0  0 10
7 1  1  5
7 0  1  9
8 1  4  6
8 0  6  7
;

Suppose 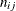$n_{ij}$ denotes the number of trials for the ith clinic and the jth treatment ( 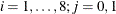$i=1,\ldots ,8; j=0,1$ ), and 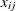$x_{ij}$ denotes the corresponding number of favorable cures. Then a reasonable model for the preceding data is the following logistic model with random effects:

$x_{ij} | u_ i \sim \mbox{Binomial}(n_{ij},p_{ij})$

and

$\eta _{ij} = \log \left( \frac{p_{ij}}{1 - p_{ij}} \right) = \beta _0 + \beta _1 t_ j + u_ i$

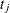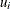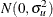The notation $t_ j$ indicates the jth treatment, and the $u_ i$ are assumed to be iid $N(0,\sigma ^2_ u)$ .

The PROC NLMIXED statements to fit this model are as follows:

proc nlmixed data=infection;
   parms beta0=-1 beta1=1 s2u=2;
   eta    = beta0 + beta1*t + u;
   expeta = exp(eta);
   p      = expeta/(1+expeta);
   model x ~ binomial(n,p);
   random u ~ normal(0,s2u) subject=clinic;
   predict eta out=eta;
   estimate '1/beta1' 1/beta1;
run;

The PROC NLMIXED statement invokes the procedure, and the PARMS statement defines the parameters and their starting values. The next three statements define 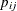$p_{ij}$ , and the MODEL statement defines the conditional distribution of 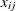$x_{ij}$ to be binomial. The RANDOM statement defines u to be the random effect with subjects defined by the clinic variable.

The PREDICT statement constructs predictions for each observation in the input data set. For this example, predictions of 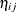$\eta _{ij}$ and approximate standard errors of prediction are output to a data set named eta. These predictions include empirical Bayes estimates of the random effects 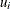$u_ i$ .

The ESTIMATE statement requests an estimate of the reciprocal of 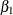$\beta _1$ .

The output for this model is as follows.

Figure 82.7: Model Information and Dimensions for Logistic-Normal Model

The NLMIXED Procedure

Specifications
Data Set	WORK.INFECTION
Dependent Variable	x
Distribution for Dependent Variable	Binomial
Random Effects	u
Distribution for Random Effects	Normal
Subject Variable	clinic
Optimization Technique	Dual Quasi-Newton
Integration Method	Adaptive Gaussian Quadrature

Dimensions
Observations Used	16
Observations Not Used	0
Total Observations	16
Subjects	8
Max Obs per Subject	2
Parameters	3
Quadrature Points	5

The "Specifications" table provides basic information about the nonlinear mixed model (Figure 82.7). For example, the distribution of the response variable, conditional on normally distributed random effects, is binomial. The "Dimensions" table provides counts of various variables. You should check this table to make sure the data set and model have been entered properly. PROC NLMIXED selects five quadrature points to achieve the default accuracy in the likelihood calculations.

Figure 82.8: Starting Values of Parameter Estimates

Initial Parameters
beta0	beta1	s2u	Negative Log Likelihood
-1	1	2	37.5945925

The "Parameters" table lists the starting point of the optimization and the negative log likelihood at the starting values (Figure 82.8).

Figure 82.9: Iteration History and Fit Statistics for Logistic-Normal Model

Iteration History
Iteration	Calls	Negative Log Likelihood	Difference	Maximum Gradient	Slope
1	4	37.3622692	0.232323	2.88208	-19.3762
2	6	37.1460375	0.216232	0.92193	-0.82852
3	9	37.0300936	0.115944	0.31590	-0.59175
4	11	37.0223017	0.007792	0.019060	-0.01615
5	13	37.0222472	0.000054	0.001743	-0.00011
6	16	37.0222466	6.57E-7	0.000091	-1.28E-6
7	19	37.0222466	5.38E-10	2.078E-6	-1.1E-9

NOTE: GCONV convergence criterion satisfied.

Fit Statistics
-2 Log Likelihood	74.0
AIC (smaller is better)	80.0
AICC (smaller is better)	82.0
BIC (smaller is better)	80.3

The "Iteration History" table indicates successful convergence in seven iterations (Figure 82.9). The "Fit Statistics" table lists some useful statistics based on the maximized value of the log likelihood.

Figure 82.10: Parameter Estimates for Logistic-Normal Model

Parameter Estimates
Parameter	Estimate	Standard Error	DF	t Value	Pr > \|t\|	95% Confidence Limits		Gradient
beta0	-1.1974	0.5561	7	-2.15	0.0683	-2.5123	0.1175	-3.1E-7
beta1	0.7385	0.3004	7	2.46	0.0436	0.02806	1.4488	-2.08E-6
s2u	1.9591	1.1903	7	1.65	0.1438	-0.8555	4.7737	-2.48E-7

The "Parameter Estimates" table indicates marginal significance of the two fixed-effects parameters (Figure 82.10). The positive value of the estimate of 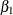$\beta _1$ indicates that the treatment significantly increases the chance of a favorable cure.

Figure 82.11: Table of Additional Estimates

Additional Estimates
Label	Estimate	Standard Error	DF	t Value	Pr > \|t\|	Alpha	Lower	Upper
1/beta1	1.3542	0.5509	7	2.46	0.0436	0.05	0.05146	2.6569

The "Additional Estimates" table displays results from the ESTIMATE statement (Figure 82.11). The estimate of 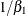$1/\beta _1$ equals 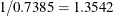$1/0.7385 = 1.3542$ and its standard error equals 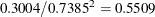$0.3004/0.7385^2 = 0.5509$ by the delta method (Billingsley 1986; Cox 1998). Note that this particular approximation produces a t-statistic identical to that for the estimate of 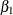$\beta _1$ . Not shown is the eta data set, which contains the original 16 observations and predictions of the 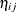$\eta _{ij}$ .