The NLMIXED Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsHierarchical Model SpecificationOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names
Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsHierarchical Model SpecificationOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names -
Examples

- References
Hierarchical Model Specification
PROC NLMIXED supports multiple RANDOM statements to accommodate nested multilevel nonlinear mixed models, starting with SAS/STAT 13.2. If you use multiple RANDOM statements, PROC NLMIXED assumes that the SUBJECT= variable from each RANDOM statement forms a containment hierarchy. In the containment hierarchy, each SUBJECT= variable is contained by another SUBJECT= variable, and the SUBJECT= variable that is contained by all SUBJECT= variables is considered "the" SUBJECT= variable. For example, consider the following three-level nested model that has three SUBJECT= variables:
|
A |
B |
C |
|
1 |
1 |
1 |
|
1 |
1 |
2 |
|
1 |
2 |
1 |
|
1 |
2 |
2 |
|
2 |
1 |
1 |
|
2 |
1 |
2 |
|
2 |
1 |
3 |
|
2 |
2 |
1 |
|
2 |
2 |
2 |
Suppose you specify a three-level nested model by using the following three RANDOM statements:
random r11 ~ normal(0,sd1) subject = A; random r21 ~ normal(0,sd2) subject = B(A); random r31 ~ normal(0,sd3) subject = C(A*B);
Then PROC NLMIXED assumes the containment hierarchy as follows. The first-level hierarchy is defined using "the" SUBJECT=
variable A. Similarly, the second-level hierarchy is defined using SUBJECT= variable B, which is nested within first level. Finally, SUBJECT= variable C defines the third-level hierarchy that is nested within both the first and second levels. In short, the SUBJECT= variable
A is "the" SUBJECT= variable. B is contained in A, and C is contained in both A and B. In this example, there are two first-level subjects that are determined using "the" SUBJECT= variable A.
Based on the preceding hierarchy specification, PROC NLMIXED’s indexing of nested subjects for each first-level subject can be visualized as follows:
![\[ \begin{array}{c c} \overbrace{\overbrace{C_{1(11)} C_{2(11)}}^{B_{1(1)}} \overbrace{C_{1(12)} C_{2(12)}}^{B_{2(1)}}}^{A_1} & \overbrace{\overbrace{C_{1(21)} C_{2(21)} C_{3(21)}}^{B_{1(2)}} \overbrace{C_{1(22)} C_{2(22)}}^{B_{2(2)}}}^{A_2} \end{array} \]](images/statug_nlmixed0189.png)
The ith subject from the first level is denoted as A , the second-level nested subjects are denoted as
, the second-level nested subjects are denoted as B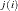 , and the third-level nested subjects are denoted as
, and the third-level nested subjects are denoted as C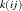 .
.
You can specify any nested structure by using the SUBJECT= syntax in PROC NLMIXED. For example, using the following three RANDOM statements, PROC NLMIXED fits a different model:
random r11 ~ normal(0,sd1) subject = C; random r21 ~ normal(0,sd2) subject = B(C); random r31 ~ normal(0,sd3) subject = A(C*B);
In this case, PROC NLMIXED processes the subjects by using SUBJECT= variable C as "the" SUBJECT= variable, and the containment hierarchy is changed as follows:
|
A |
B |
C |
|
1 |
1 |
1 |
|
1 |
1 |
2 |
|
1 |
2 |
1 |
|
1 |
2 |
2 |
|
2 |
1 |
1 |
|
2 |
1 |
2 |
|
2 |
1 |
3 |
|
2 |
2 |
1 |
|
2 |
2 |
2 |
|
C |
B |
A |
|
1 |
1 |
1 |
|
1 |
1 |
2 |
|
1 |
2 |
1 |
|
1 |
2 |
2 |
|
2 |
1 |
1 |
|
2 |
1 |
2 |
|
2 |
2 |
1 |
|
2 |
2 |
2 |
|
3 |
1 |
2 |
Again, PROC NLMIXED’s indexing of the nested subjects in this containment hierarchy can be visualized as follows:
![\[ \begin{array}{c c c} \overbrace{\overbrace{A_{1(11)} A_{2(11)}}^{B_{1(1)}} \overbrace{A_{1(12)} A_{2(12)}}^{B_{2(1)}}}^{C_1} & \overbrace{\overbrace{A_{1(21)} A_{2(21)}}^{B_{1(2)}} \overbrace{A_{1(22)} A_{2(22)}}^{B_{2(2)}}}^{C_2} & \overbrace{\overbrace{A_{1(31)}}^{B_{1(3)}}}^{C_3} \end{array} \]](images/statug_nlmixed0194.png)
Here, PROC NLMIXED assumes that C is "the" SUBJECT=
variable. B is contained in C, and A is contained in C and B. In this case, there are three first-level subjects that are determined using "the" SUBJECT= variable C.
As explained before, in this case, the ith subject from the first level is denoted as C , the second-level nested subjects are denoted as
, the second-level nested subjects are denoted as B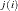 and for third level, the nested subjects are denoted as
and for third level, the nested subjects are denoted as A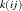 .
.
Note that the containment hierarchy could potentially create more subjects than the unique number of subjects. For example,
consider the following table, in which A is "the" SUBJECT= variable and B is nested within the subject A:
|
A |
B |
|
a |
1 |
|
a |
2 |
|
b |
1 |
|
b |
2 |
|
c |
1 |
|
c |
2 |
Even though the SUBJECT = B variable has only two unique subjects (1 and 2), when the containment hierarchy that is specified along with B is nested within A, PROC NLMIXED creates six nested B subjects. These nested subjects can be denoted as 1(a), 2(a), 1(b), 2(b), 1(c), and 2(c).
PROC NLMIXED does not support noncontainment hierarchy (or non-nested) models. For example, the following statements are not
supported, because subject C is not nested within B and A:
random r11 ~ normal(0,sd1) subject = A; random r21 ~ normal(0,sd2) subject = B(A); random r31 ~ normal(0,sd3) subject = C;