The NLMIXED Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsHierarchical Model SpecificationOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names
Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsHierarchical Model SpecificationOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names -
Examples

- References
Example 82.3 Probit-Normal Model with Ordinal Data
The data for this example are from Ezzet and Whitehead (1991), who describe a crossover experiment on two groups of patients using two different inhaler devices (A and B). Patients from group 1 used device A for one week and then device B for another week. Patients from group 2 used the devices in reverse order. The data entered as a SAS data set are as follows:
data inhaler; input clarity group time freq @@; gt = group*time; sub = floor((_n_+1)/2); datalines; 1 0 0 59 1 0 1 59 1 0 0 35 2 0 1 35 1 0 0 3 3 0 1 3 1 0 0 2 4 0 1 2 2 0 0 11 1 0 1 11 2 0 0 27 2 0 1 27 2 0 0 2 3 0 1 2 2 0 0 1 4 0 1 1 4 0 0 1 1 0 1 1 4 0 0 1 2 0 1 1 1 1 0 63 1 1 1 63 1 1 0 13 2 1 1 13 2 1 0 40 1 1 1 40 2 1 0 15 2 1 1 15 3 1 0 7 1 1 1 7 3 1 0 2 2 1 1 2 3 1 0 1 3 1 1 1 4 1 0 2 1 1 1 2 4 1 0 1 3 1 1 1 ;
The response measurement, clarity, is the patients’ assessment on the clarity of the leaflet instructions for the devices. The clarity variable is on an ordinal scale, with 1=easy, 2=only clear after rereading, 3=not very clear, and 4=confusing. The group variable indicates the treatment group, and the time variable indicates the time of measurement. The freq variable indicates the number of patients with exactly the same responses. A variable gt is created to indicate a group-by-time interaction, and a variable sub is created to indicate patients.
As in the previous example and in Hedeker and Gibbons (1994), assume an underlying latent continuous variable, here with the form
![\[ y_{ij} = \beta _0 + \beta _1 g_ i + \beta _2 t_ j + \beta _3 g_ i t_ j + u_ i + e_{ij} \]](images/statug_nlmixed0353.png)
where i indexes patient and j indexes the time period, 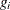 indicates groups,
indicates groups, 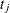 indicates time,
indicates time, 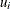 is a patient-level normal random effect, and
is a patient-level normal random effect, and 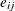 are iid normal errors. The
are iid normal errors. The 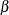 s are unknown coefficients to be estimated.
s are unknown coefficients to be estimated.
Instead of observing 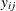 , however, you observe only whether it falls in one of the four intervals: (
, however, you observe only whether it falls in one of the four intervals: (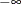 , 0), (0, I1), (I1, I1 + I2), or (I1 + I2,
, 0), (0, I1), (I1, I1 + I2), or (I1 + I2, 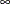 ), where I1 and I2 are both positive. The resulting category is the value assigned to the
), where I1 and I2 are both positive. The resulting category is the value assigned to the clarity variable.
The following code sets up and fits this ordinal probit model:
proc nlmixed data=inhaler corr ecorr;
parms b0=0 b1=0 b2=0 b3=0 sd=1 i1=1 i2=1;
bounds i1 > 0, i2 > 0;
eta = b0 + b1*group + b2*time + b3*gt + u;
if (clarity=1) then p = probnorm(-eta);
else if (clarity=2) then
p = probnorm(i1-eta) - probnorm(-eta);
else if (clarity=3) then
p = probnorm(i1+i2-eta) - probnorm(i1-eta);
else p = 1 - probnorm(i1+i2-eta);
if (p > 1e-8) then ll = log(p);
else ll = -1e20;
model clarity ~ general(ll);
random u ~ normal(0,sd*sd) subject=sub;
replicate freq;
estimate 'thresh2' i1;
estimate 'thresh3' i1 + i2;
estimate 'icc' sd*sd/(1+sd*sd);
run;
The PROC NLMIXED statement specifies the input data set and requests correlations both for the parameter estimates (CORR option) and for the additional estimates specified with ESTIMATE statements (ECORR option).
The parameters as defined in the PARMS statement are as follows: b0 (overall intercept), b1 (group main effect), B2 (time main effect), b3 (group-by-time interaction), sd (standard deviation of the random effect), i1 (increment between first and second thresholds), and i2 (increment between second and third thresholds). The BOUNDS
statement restricts i1 and i2 to be positive.
The SAS programming statements begin by defining the linear predictor eta, which is a linear combination of the b parameters and a single random effect u. The next statements define the ordinal likelihood according to the clarity variable, eta, and the increment variables. An error trap is included in case the likelihood becomes too small.
A general log-likelihood specification is used in the MODEL
statement, and the RANDOM
statement defines the random effect u to have standard deviation sd and subject variable sub. The REPLICATE
statement indicates that data for each subject should be replicated according to the freq variable.
The ESTIMATE statements specify the second and third thresholds in terms of the increment variables (the first threshold is assumed to equal zero for model identifiability). Also computed is the intraclass correlation.
The output is as follows.
Output 82.3.1: Specifications for Ordinal Data Model
| Specifications | |
|---|---|
| Data Set | WORK.INHALER |
| Dependent Variable | clarity |
| Distribution for Dependent Variable | General |
| Random Effects | u |
| Distribution for Random Effects | Normal |
| Subject Variable | sub |
| Replicate Variable | freq |
| Optimization Technique | Dual Quasi-Newton |
| Integration Method | Adaptive Gaussian Quadrature |
The "Specifications" table echoes some primary information specified for this nonlinear mixed model (Output 82.3.1). Because the log-likelihood function was expressed with SAS programming statements, the distribution is displayed as General in the "Specifications" table.
The "Dimensions" table reveals a total of 286 subjects, which is the sum of the values of the FREQ variable for the second time point. Five quadrature points are selected for log-likelihood evaluation (Output 82.3.2).
Output 82.3.2: Dimensions Table for Ordinal Data Model
Output 82.3.3: Parameter Starting Values and Negative Log Likelihood
The "Parameters" table lists the simple starting values for this problem (Output 82.3.3). The "Iteration History" table indicates successful convergence in 13 iterations (Output 82.3.4).
Output 82.3.4: Iteration History
| Iteration History | |||||
|---|---|---|---|---|---|
| Iteration | Calls | Negative Log Likelihood |
Difference | Maximum Gradient |
Slope |
| 1 | 4 | 476.3825 | 62.10176 | 43.7506 | -1431.40 |
| 2 | 7 | 463.2282 | 13.15431 | 14.2465 | -106.753 |
| 3 | 9 | 458.5281 | 4.70008 | 48.3132 | -33.0389 |
| 4 | 11 | 450.9757 | 7.552383 | 22.6010 | -40.9954 |
| 5 | 14 | 448.0127 | 2.963033 | 14.8688 | -16.7453 |
| 6 | 17 | 447.2452 | 0.767549 | 7.77419 | -2.26743 |
| 7 | 19 | 446.7277 | 0.517483 | 3.79353 | -1.59278 |
| 8 | 22 | 446.5183 | 0.209396 | 0.86864 | -0.37801 |
| 9 | 26 | 446.5145 | 0.003745 | 0.32857 | -0.02356 |
| 10 | 29 | 446.5133 | 0.001187 | 0.056778 | -0.00183 |
| 11 | 32 | 446.5133 | 0.000027 | 0.010785 | -0.00004 |
| 12 | 35 | 446.5133 | 3.956E-6 | 0.004922 | -5.41E-6 |
| 13 | 38 | 446.5133 | 1.989E-7 | 0.000470 | -4E-7 |
Output 82.3.5: Fit Statistics for Ordinal Data Model
The "Fit Statistics" table lists the log likelihood and information criteria for model comparisons (Output 82.3.5).
Output 82.3.6: Parameter Estimates at Convergence
| Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | Estimate | Standard Error |
DF | t Value | Pr > |t| | 95% Confidence Limits | Gradient | |
| b0 | -0.6364 | 0.1342 | 285 | -4.74 | <.0001 | -0.9006 | -0.3722 | 0.000470 |
| b1 | 0.6007 | 0.1770 | 285 | 3.39 | 0.0008 | 0.2523 | 0.9491 | 0.000265 |
| b2 | 0.6015 | 0.1582 | 285 | 3.80 | 0.0002 | 0.2900 | 0.9129 | 0.000080 |
| b3 | -1.4817 | 0.2385 | 285 | -6.21 | <.0001 | -1.9512 | -1.0122 | 0.000102 |
| sd | 0.6599 | 0.1312 | 285 | 5.03 | <.0001 | 0.4017 | 0.9181 | -0.00009 |
| i1 | 1.7450 | 0.1474 | 285 | 11.84 | <.0001 | 1.4548 | 2.0352 | 0.000202 |
| i2 | 0.5985 | 0.1427 | 285 | 4.19 | <.0001 | 0.3176 | 0.8794 | 0.000087 |
The "Parameter Estimates" table indicates significance of all the parameters (Output 82.3.6).
Output 82.3.7: Threshold and Intraclass Correlation Estimates
The "Additional Estimates" table displays results from the ESTIMATE statements (Output 82.3.7).