The NLMIXED Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsHierarchical Model SpecificationOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names
Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsHierarchical Model SpecificationOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names -
Examples

- References
Modeling Assumptions and Notation
PROC NLMIXED operates under the following general framework for nonlinear mixed models. Assume that you have an observed data
vector 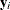 for each of i subjects,
for each of i subjects, 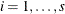 . The
. The 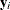 are assumed to be independent across i, but within-subject covariance is likely to exist because each of the elements of
are assumed to be independent across i, but within-subject covariance is likely to exist because each of the elements of 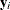 is measured on the same subject. As a statistical mechanism for modeling this within-subject covariance, assume that there
exist latent random-effect vectors
is measured on the same subject. As a statistical mechanism for modeling this within-subject covariance, assume that there
exist latent random-effect vectors 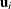 of small dimension (typically one or two) that are also independent across i. Assume also that an appropriate model linking
of small dimension (typically one or two) that are also independent across i. Assume also that an appropriate model linking 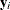 and
and 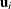 exists, leading to the joint probability density function
exists, leading to the joint probability density function
![\[ p(\mb{y}_ i | \mb{X}_ i, \bphi , \mb{u}_ i) q(\mb{u}_ i | \bxi ) \]](images/statug_nlmixed0114.png)
where 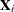 is a matrix of observed explanatory variables and
is a matrix of observed explanatory variables and 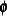 and
and 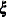 are vectors of unknown parameters.
are vectors of unknown parameters.
Let ![$\btheta = [\bphi , \bxi ]$](images/statug_nlmixed0118.png) and assume that it is of dimension n. Then inferences about
and assume that it is of dimension n. Then inferences about 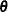 are based on the marginal likelihood function
are based on the marginal likelihood function
![\[ m(\btheta ) = \prod _{i=1}^ s \int p(\mb{y}_ i | \mb{X}_ i, \bphi , \mb{u}_ i) q(\mb{u}_ i | \bxi ) d \mb{u}_ i \]](images/statug_nlmixed0120.png)
In particular, the function
![\[ f(\btheta ) = - \log m(\btheta ) \]](images/statug_nlmixed0121.png)
is minimized over 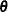 numerically in order to estimate
numerically in order to estimate 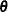 , and the inverse Hessian (second derivative) matrix at the estimates provides an approximate variance-covariance matrix for
the estimate of
, and the inverse Hessian (second derivative) matrix at the estimates provides an approximate variance-covariance matrix for
the estimate of 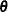 . The function
. The function 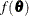 is referred to both as the negative log likelihood function and as the objective function for optimization.
is referred to both as the negative log likelihood function and as the objective function for optimization.
As an example of the preceding general framework, consider the nonlinear growth curve example in the section Getting Started: NLMIXED Procedure. Here, the conditional distribution 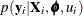 is normal with mean
is normal with mean
![\[ \frac{b_1 + u_{i1}}{1 + \exp [-(d_{ij} - b_2)/ b_3]} \]](images/statug_nlmixed0124.png)
and variance 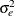 ; thus
; thus ![$\bphi = [b_1,b_2,b_3,\sigma ^2_ e]$](images/statug_nlmixed0126.png) . Also,
. Also, 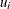 is a scalar and
is a scalar and 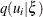 is normal with mean 0 and variance
is normal with mean 0 and variance 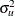 ; thus
; thus 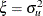 .
.
The following additional notation is also found in this chapter. The quantity 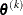 refers to the parameter vector at the kth iteration, the vector
refers to the parameter vector at the kth iteration, the vector 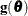 refers to the gradient vector
refers to the gradient vector 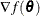 , and the matrix
, and the matrix 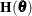 refers to the Hessian
refers to the Hessian 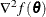 . Other symbols are used to denote various constants or option values.
. Other symbols are used to denote various constants or option values.
Nested Multilevel Nonlinear Mixed Models
The general framework for nested multilevel nonlinear mixed models in cases of two levels can be explained as follows. Let
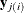 be the response vector observed on subject j that is nested within subject i, where j is commonly referred as the second-level subject and i is the first-level subject. There are s first-level subjects, and each has
be the response vector observed on subject j that is nested within subject i, where j is commonly referred as the second-level subject and i is the first-level subject. There are s first-level subjects, and each has  second-level subjects that are nested within. An example is
second-level subjects that are nested within. An example is 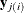 , which are the heights of students in class j of school i, where
, which are the heights of students in class j of school i, where 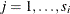 for each i and
for each i and 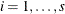 . Suppose there exist latent random-effect vectors
. Suppose there exist latent random-effect vectors 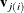 and
and 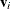 of small dimensions for modeling within subject covariance. Assume also that an appropriate model that links
of small dimensions for modeling within subject covariance. Assume also that an appropriate model that links 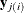 and
and 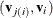 exists, and if you use the notation
exists, and if you use the notation 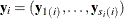 ,
, 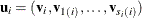 , and
, and 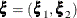 , the joint density function in terms of the first-level subject can be expressed as
, the joint density function in terms of the first-level subject can be expressed as
![\[ p(\mb{y}_ i | \mb{X}_ i, \bphi , \mb{u}_ i) q(\mb{u}_ i | \bxi ) = \left( \prod _{j=1}^{s_ i} p(\mb{y}_{j(i)} | \mb{X}_ i,\bphi ,\mb{v}_ i,\mb{v}_{j(i)}) q_2(\mb{v}_{j(i)} | \bxi _2) \right) q_1(\mb{v}_ i | \bxi _1) \]](images/statug_nlmixed0143.png)
As defined in the previous section, the marginal likelihood function where ![$\btheta = [\bphi , \bxi ]$](images/statug_nlmixed0118.png) is
is
![\[ m(\btheta ) = \prod _{i=1}^ s \int p(\mb{y}_ i | \mb{X}_ i, \bphi , \mb{u}_ i) q(\mb{u}_ i | \bxi ) d \mb{u}_ i \]](images/statug_nlmixed0120.png)
Again, the function
![\[ f(\btheta ) = - \log m(\btheta ) \]](images/statug_nlmixed0121.png)
is minimized over 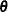 numerically in order to estimate
numerically in order to estimate 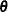 . Models that have more than two levels follow similar notation.
. Models that have more than two levels follow similar notation.