The NLMIXED Procedure

Prediction

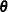The nonlinear mixed model is a useful tool for statistical prediction. Assuming a prediction is to be made regarding the ith subject, suppose that $f(\btheta ,\mb{u}_ i)$ is a differentiable function predicting some quantity of interest. Recall that $\btheta$ denotes the vector of unknown parameters and 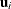$\mb{u}_ i$ denotes the vector of random effects for the ith subject. 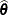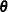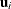A natural point prediction is $f(\widehat{\btheta },\widehat{\mb{u}}_ i)$ , where $\widehat{\btheta }$ is the maximum likelihood estimate of $\btheta$ and $\widehat{\mb{u}}_ i$ is the empirical Bayes estimate of $\mb{u}_ i$ described previously in the section Integral Approximations.

An approximate prediction variance matrix for $(\widehat{\btheta },\widehat{\mb{u}}_ i)$ is

$\bP = \left[ \begin{array}{ll} \widehat{\mb{H}}^{-1} & \widehat{\mb{H}}^{-1} \left( \frac{\partial \widehat{\mb{u}}_ i}{\partial \btheta } \right)^\prime \\ \left( \frac{\partial \widehat{\mb{u}}_ i}{\partial \btheta } \right) \widehat{\mb{H}}^{-1} & \widehat{\bGamma }^{-1} + \left( \frac{\partial \widehat{\mb{u}}_ i}{\partial \btheta } \right) \widehat{\mb{H}}^{-1} \left( \frac{\partial \widehat{\mb{u}}_ i}{\partial \btheta } \right)^\prime \end{array} \right]$

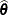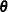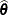where $\widehat{\mb{H}}$ is the approximate Hessian matrix from the optimization for $\widehat{\btheta }$ , $\widehat{\bGamma }$ is the approximate Hessian matrix from the optimization for $\widehat{\mb{u}}_ i$ , and $(\partial \widehat{\mb{u}}_ i/\partial \btheta )$ is the derivative of $\widehat{\mb{u}}_ i$ with respect to $\btheta$ , evaluated at $(\widehat{\btheta },\widehat{\mb{u}}_ i)$ . The approximate variance matrix for $\widehat{\btheta }$ is the standard one discussed in the previous section, and that for $\widehat{\mb{u}}_ i$ is an approximation to the conditional mean squared error of prediction described by Booth and Hobert (1998).

The prediction variance for a general scalar function $f(\btheta ,\mb{u}_ i)$ is defined as the expected squared difference $E[f(\widehat{\btheta },\widehat{\mb{u}}_ i) - f(\btheta ,\mb{u}_ i)]^2.$ PROC NLMIXED computes an approximation to it as follows. The derivative of $f(\btheta ,\mb{u}_ i)$ is computed with respect to each element of $(\btheta ,\mb{u}_ i)$ and evaluated at $(\widehat{\btheta },\widehat{\mb{u}}_ i)$ . 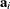If $\mb{a}_ i$ is the resulting vector, then the approximate prediction variance is $\mb{a}^\prime _ i \mb{P} \mb{a}_ i$ . This approximation is known as the delta method (Billingsley 1986; Cox 1998).