The GAMPL Procedure

The factors that affect how you choose an optimization technique for a particular problem are complex. Although the default technique works well for most problems, you might occasionally benefit from trying several different techniques.

For many optimization problems, computing the gradient takes more computer time than computing the function value. Computing the Hessian sometimes takes much more computer time and memory than computing the gradient, especially when there are many decision variables. Unfortunately, optimization techniques that do not use some kind of Hessian approximation usually require many more iterations than techniques that use a Hessian matrix; as a result, the total run time of these techniques is often longer. Techniques that do not use the Hessian also tend to be less reliable. For example, they can terminate more easily at stationary points than at global optima.

Table 42.12 shows which derivatives are required for each optimization technique.

The second-order derivative techniques (TRUREG, NEWRAP, and NRRIDG) are best for small problems for which the Hessian matrix is not expensive to compute. Sometimes the NRRIDG technique can be faster than the TRUREG technique, but TRUREG can be more stable. The NRRIDG technique requires only one matrix with 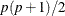double words, where p denotes the number of parameters in the optimization. TRUREG and NEWRAP require two such matrices.

The QUANEW and DBLDOG first-order derivative techniques are best for medium-sized problems for which the objective function and the gradient can be evaluated much faster than the Hessian. In general, the QUANEW and DBLDOG techniques require more iterations than TRUREG, NRRIDG, and NEWRAP, but each iteration can be much faster. The QUANEW and DBLDOG techniques require only the gradient to update an approximate Hessian, and they require slightly less memory than TRUREG or NEWRAP.

The CONGRA first-order derivative technique is best for large problems for which the objective function and the gradient can be computed much faster than the Hessian and for which too much memory is required to store the (approximate) Hessian. In general, the CONGRA technique requires more iterations than QUANEW or DBLDOG, but each iteration can be much faster. Because CONGRA requires only a factor of p double-word memory, many large applications can be solved only by CONGRA.

The no-derivative technique NMSIMP is best for small problems for which derivatives are not continuous or are very difficult to compute.

Each optimization technique uses one or more convergence criteria that determine when it has converged. A technique is considered to have converged when any one of the convergence criteria is satisfied. For example, under the default settings, the QUANEW technique converges if the value of the ABSGCONV= option is less than 1E–5, the value of the FCONV= option is less than 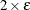, or the value of the GCONV= option is less than 1E–8.

By default, the GAMPL procedure applies the NEWRAP technique to optimization for selecting smoothing parameters by using the performance iteration method. For the outer iteration method, the GAMPL procedure applies the QUANEW technique for selecting smoothing parameters.