The GAMPL Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Missing ValuesThin-Plate Regression SplinesGeneralized Additive ModelsModel Evaluation CriteriaFitting AlgorithmsDegrees of FreedomModel InferenceDispersion ParameterTests for Smoothing ComponentsComputational Method: MultithreadingChoosing an Optimization TechniqueDisplayed OutputODS Table NamesODS Graphics
Missing ValuesThin-Plate Regression SplinesGeneralized Additive ModelsModel Evaluation CriteriaFitting AlgorithmsDegrees of FreedomModel InferenceDispersion ParameterTests for Smoothing ComponentsComputational Method: MultithreadingChoosing an Optimization TechniqueDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Model Inference
Wahba (1983) proposes a Bayesian covariance matrix for parameter estimates 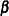 by interpreting a smoothing spline as a posterior mean. Nychka (1988) shows that the derived Bayesian posterior confidence limits work well from frequentist viewpoints. The Bayesian posterior
covariance matrix for the parameters is
by interpreting a smoothing spline as a posterior mean. Nychka (1988) shows that the derived Bayesian posterior confidence limits work well from frequentist viewpoints. The Bayesian posterior
covariance matrix for the parameters is
![\[ \bV _{\bbeta }=(\bX ’\bW \bX +\bS _{\blambda })^{-1}\sigma ^2 \]](images/statug_hpgam0193.png)
The posterior distribution for 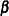 is thus
is thus
![\[ \bbeta |\mb{y} \sim N(\hat{\bbeta },\bV _{\bbeta }) \]](images/statug_hpgam0194.png)
For a particular point whose design row is vector  , the prediction is
, the prediction is  and the standard error is
and the standard error is  . The Bayesian posterior confidence limits are thus
. The Bayesian posterior confidence limits are thus
![\[ \left(\mb{x}\hat{\bbeta } \pm z_{\alpha /2} \sqrt {\mb{x}\bV _{\bbeta }\mb{x}’}\right) \]](images/statug_hpgam0197.png)
where  is the
is the  quantile of the standard normal distribution.
quantile of the standard normal distribution.
For the jth spline term, the prediction for the component is formed by  , where
, where  is a row vector of zeros except for columns that correspond to basis expansions of the jth spline term. And the standard error for the component is
is a row vector of zeros except for columns that correspond to basis expansions of the jth spline term. And the standard error for the component is  .
.