The GAMPL Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Missing ValuesThin-Plate Regression SplinesGeneralized Additive ModelsModel Evaluation CriteriaFitting AlgorithmsDegrees of FreedomModel InferenceDispersion ParameterTests for Smoothing ComponentsComputational Method: MultithreadingChoosing an Optimization TechniqueDisplayed OutputODS Table NamesODS Graphics
Missing ValuesThin-Plate Regression SplinesGeneralized Additive ModelsModel Evaluation CriteriaFitting AlgorithmsDegrees of FreedomModel InferenceDispersion ParameterTests for Smoothing ComponentsComputational Method: MultithreadingChoosing an Optimization TechniqueDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Degrees of Freedom
Let 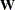 be the adjusted weight matrix at convergence, and let
be the adjusted weight matrix at convergence, and let 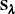 be the roughness penalty matrix with selected smoothing parameters. The degrees of freedom matrix is defined as in Wood (2006):
be the roughness penalty matrix with selected smoothing parameters. The degrees of freedom matrix is defined as in Wood (2006):
![\[ \bF = (\bX ’\bW \bX +\bS _{\blambda })^{-1}\bX ’\bW \bX \]](images/statug_hpgam0183.png)
Given the adjusted response  , the parameter estimate is shown to be
, the parameter estimate is shown to be 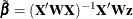 for the model without penalization, and the parameter estimate is
for the model without penalization, and the parameter estimate is 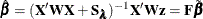 with penalization.
with penalization. 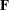 is thus the matrix that projects or maps the unpenalized parameter estimates to the penalized ones.
is thus the matrix that projects or maps the unpenalized parameter estimates to the penalized ones.
The model degrees of freedom is given as
![\[ \mathrm{df} = \mathrm{tr}(\bF ) \]](images/statug_hpgam0188.png)
And the degrees of freedom for error is given as
![\[ \mathrm{df}_ r = n - 2\mathrm{df} + \mathrm{tr}(\bF \bF ) \]](images/statug_hpgam0189.png)
For the jth spline term, the degrees of freedom for the component is defined to be the trace of the submatrix of 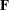 that corresponds to parameter estimates
that corresponds to parameter estimates 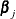 :
:
![\[ \mathrm{df}_ j = \mathrm{tr}(\bF _ j) \]](images/statug_hpgam0191.png)
The degrees of freedom for the smoothing component test of the jth term is defined similarly as
![\[ \mathrm{df}_ j^ t = 2\mathrm{df}_ j-\mathrm{tr}((\bF \bF )_ j) \]](images/statug_hpgam0192.png)