The FMM Procedure
Overdispersion
Overdispersion is the condition by which the data are more dispersed than is permissible under a reference model. Overdispersion arises only if the variability a model can capture is limited (for example, because of a functional relationship between mean and variance). For example, a model for normal data can never be overdispersed in this sense, although the reasons that lead to overdispersion also negatively affect a misspecified model for normal data. For example, omitted variables increase the residual variance estimate because variability that should have been modeled through changes in the mean is now "picked up" as error variability.
Overdispersion is important because an overdispersed model can lead to misleading inferences and conclusions. However, diagnosing and remedying overdispersion is complicated. In order to handle it appropriately, the source of overdispersion must be identified. For example, overdispersion can arise from any of the following conditions alone or in combination:
-
omitted variables and model effects
-
omitted random effects (a source of random variation is not being modeled or is modeled as a fixed effect)
-
correlation among the observations
-
incorrect distributional assumptions
-
incorrectly specified mean-variance relationships
-
outliers in the data
As discussed in the previous section, introducing randomness into a system increases its variability. Mixture, mixed, and mixing models have thus been popular in modeling data that appear overdispersed. Finite mixture models are particularly powerful in this regard, because even low-order mixtures of basic, symmetric distributions (such as two- or three-component mixtures of normal or t distributions) enable you to model data with multiple modes, heavy tails, and skewness. In addition, the latent variable S provides a natural way to accommodate omitted, unobservable variables into the model.
One approach to remedy overdispersion is to apply simple modifications of the variance function of the reference model. For
example, with binomial-type data this approach replaces the variance of the binomial count variable 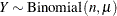 ,
, ![$\mr{Var}[Y] = n\times \mu (1-\mu )$](images/statug_fmm0170.png) with a scaled version,
with a scaled version, 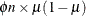 , where
, where  is called an overdispersion parameter,
is called an overdispersion parameter, 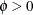 .
.
In addressing overdispersion problems, it is important to tackle the problem at its root. A missing scale factor on the variance function is hardly ever the root cause of overdispersion; it is only the easiest remedy.
