The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement -
Details
 Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis - References
No algorithm for optimizing general nonlinear functions exists that can always find the global optimum for a general nonlinear
minimization problem in a reasonable amount of time. Since no single optimization technique is invariably superior to others,
PROC CALIS provides a variety of optimization techniques that work well in various circumstances. However, you can devise
problems for which none of the techniques in PROC CALIS can find the correct solution. All optimization techniques in PROC
CALIS use ![]() memory except the conjugate gradient methods, which use only
memory except the conjugate gradient methods, which use only ![]() of memory and are designed to optimize problems with many parameters.
of memory and are designed to optimize problems with many parameters.
The PROC CALIS statement NLOPTIONS can be especially helpful for tuning applications with nonlinear equality and inequality constraints on the parameter estimates. Some of the options available in NLOPTIONS can also be invoked as PROC CALIS options. The NLOPTIONS statement can specify almost the same options as the SAS/OR NLP procedure.
Nonlinear optimization requires the repeated computation of the following:
For the criteria used by PROC CALIS, computing the gradient takes more computer time than computing the function value, and computing the Hessian takes much more computer time and memory than computing the gradient, especially when there are many parameters to estimate. Unfortunately, optimization techniques that do not use the Hessian usually require many more iterations than techniques that do use the (approximate) Hessian, and so they are often slower. Techniques that do not use the Hessian also tend to be less reliable (for example, they might terminate at local rather than global optima).
The available optimization techniques are displayed in the following table and can be chosen by the OMETHOD=name option.
|
OMETHOD= |
Optimization Technique |
|---|---|
|
LEVMAR |
Levenberg-Marquardt method |
|
TRUREG |
Trust-region method |
|
NEWRAP |
Newton-Raphson method with line search |
|
NRRIDG |
Newton-Raphson method with ridging |
|
QUANEW |
Quasi-Newton methods (DBFGS, DDFP, BFGS, DFP) |
|
DBLDOG |
Double-dogleg method (DBFGS, DDFP) |
|
CONGRA |
Conjugate gradient methods (PB, FR, PR, CD) |
The following table shows, for each optimization technique, which derivatives are needed (first-order or second-order) and what kind of constraints (boundary, linear, or nonlinear) can be imposed on the parameters.
|
Derivatives |
Constraints |
||||
|---|---|---|---|---|---|
|
OMETHOD= |
First Order |
Second Order |
Boundary |
Linear |
Nonlinear |
|
LEVMAR |
x |
x |
x |
x |
- |
|
TRUREG |
x |
x |
x |
x |
- |
|
NEWRAP |
x |
x |
x |
x |
- |
|
NRRIDG |
x |
x |
x |
x |
- |
|
QUANEW |
x |
- |
x |
x |
x |
|
DBLDOG |
x |
- |
x |
x |
- |
|
CONGRA |
x |
- |
x |
x |
- |
The Levenberg-Marquardt, trust-region, and Newton-Raphson techniques are usually the most reliable, work well with boundary and general linear constraints, and generally converge after a few iterations to a precise solution. However, these techniques need to compute a Hessian matrix in each iteration. Computing the approximate Hessian in each iteration can be very time- and memory-consuming, especially for large problems (more than 200 parameters, depending on the computer used). For large problems, a quasi-Newton technique, especially with the BFGS update, can be far more efficient.
For a poor choice of initial values, the Levenberg-Marquardt method seems to be more reliable.
If memory problems occur, you can use one of the conjugate gradient techniques, but they are generally slower and less reliable than the methods that use second-order information.
There are several options to control the optimization process. You can specify various termination criteria. You can specify the GCONV= option to specify a relative gradient termination criterion. If there are active boundary constraints, only those gradient components that correspond to inactive constraints contribute to the criterion. When you want very precise parameter estimates, the GCONV= option is useful. Other criteria that use relative changes in function values or parameter estimates in consecutive iterations can lead to early termination when active constraints cause small steps to occur. The small default value for the FCONV= option helps prevent early termination. Using the MAXITER= and MAXFUNC= options enables you to specify the maximum number of iterations and function calls in the optimization process. These limits are especially useful in combination with the INMODEL= and OUTMODEL= options; you can run a few iterations at a time, inspect the results, and decide whether to continue iterating.
The algorithm used for nonlinearly constrained quasi-Newton optimization is an efficient modification of Powell’s Variable Metric Constrained WatchDog (VMCWD) algorithm (Powell, 1978a, 1978b, 1982a, 1982b) A similar but older algorithm (VF02AD) is part of the Harwell library. Both VMCWD and VF02AD use Fletcher’s VE02AD algorithm (also part of the Harwell library) for positive definite quadratic programming. The PROC CALIS QUANEW implementation uses a quadratic programming subroutine that updates and downdates the approximation of the Cholesky factor when the active set changes. The nonlinear QUANEW algorithm is not a feasible point algorithm, and the value of the objective function might not necessarily decrease (minimization) or increase (maximization) monotonically. Instead, the algorithm tries to reduce a linear combination of the objective function and constraint violations, called the merit function.
The following are similarities and differences between this algorithm and VMCWD:
-
A modification of this algorithm can be performed by specifying VERSION=1, which replaces the update of the Lagrange vector
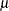 with the original update of Powell (1978a, 1978b), which is used in VF02AD. This can be helpful for some applications with linearly dependent active constraints.
with the original update of Powell (1978a, 1978b), which is used in VF02AD. This can be helpful for some applications with linearly dependent active constraints.
-
If the VERSION= option is not specified or VERSION=2 is specified, the evaluation of the Lagrange vector
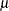 is performed in the same way as Powell (1982a, 1982b) describes.
is performed in the same way as Powell (1982a, 1982b) describes.
-
Instead of updating an approximate Hessian matrix, this algorithm uses the dual BFGS (or DFP) update that updates the Cholesky factor of an approximate Hessian. If the condition of the updated matrix gets too bad, a restart is done with a positive diagonal matrix. At the end of the first iteration after each restart, the Cholesky factor is scaled.
-
The Cholesky factor is loaded into the quadratic programming subroutine, automatically ensuring positive definiteness of the problem. During the quadratic programming step, the Cholesky factor of the projected Hessian matrix
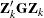 and the QT decomposition are updated simultaneously when the active set changes. See Gill et al. (1984) for more information.
and the QT decomposition are updated simultaneously when the active set changes. See Gill et al. (1984) for more information.
-
The line-search strategy is very similar to that of Powell (1982a, 1982b). However, this algorithm does not call for derivatives during the line search; hence, it generally needs fewer derivative calls than function calls. The VMCWD algorithm always requires the same number of derivative and function calls. It was also found in several applications of VMCWD that Powell’s line-search method sometimes uses steps that are too long during the first iterations. In those cases, you can use the INSTEP= option specification to restrict the step length
 of the first iterations.
of the first iterations.
-
The watchdog strategy is similar to that of Powell (1982a, 1982b). However, this algorithm does not return automatically after a fixed number of iterations to a former better point. A return here is further delayed if the observed function reduction is close to the expected function reduction of the quadratic model.
-
Although Powell’s termination criterion still is used (as FCONV2), the QUANEW implementation uses two additional termination criteria (GCONV and ABSGCONV).
This algorithm is automatically invoked when you specify the NLINCON statement. The nonlinear QUANEW algorithm needs the Jacobian matrix of the first-order derivatives (constraints normals) of the constraints:
where nc is the number of nonlinear constraints for a given point x.
You can specify two update formulas with the UPDATE= option:
This algorithm uses its own line-search technique. All options and parameters (except the INSTEP=
option) controlling the line search in the other algorithms do not apply here. In several applications, large steps in the
first iterations are troublesome. You can specify the INSTEP=
option to impose an upper bound for the step size ![]() during the first five iterations. The values of the LCSINGULAR=, LCEPSILON=, and LCDEACT= options (which control the processing
of linear and boundary constraints) are valid only for the quadratic programming subroutine used in each iteration of the
nonlinear constraints QUANEW algorithm.
during the first five iterations. The values of the LCSINGULAR=, LCEPSILON=, and LCDEACT= options (which control the processing
of linear and boundary constraints) are valid only for the quadratic programming subroutine used in each iteration of the
nonlinear constraints QUANEW algorithm.
The optimization and iteration histories are displayed by default because it is important to check for possible convergence problems. The optimization history includes the following summary of information about the initial state of the optimization:
-
the number of constraints that are active at the starting point, or more precisely, the number of constraints that are currently members of the working set. If this number is followed by a plus sign, there are more active constraints, of which at least one is temporarily released from the working set due to negative Lagrange multipliers.
-
the value of the objective function at the starting point
-
if the (projected) gradient is available, the value of the largest absolute (projected) gradient element
-
for the TRUREG and LEVMAR subroutines, the initial radius of the trust region around the starting point
The optimization history ends with some information concerning the optimization result:
-
the number of constraints that are active at the final point, or more precisely, the number of constraints that are currently members of the working set. If this number is followed by a plus sign, there are more active constraints, of which at least one is temporarily released from the working set due to negative Lagrange multipliers.
-
the value of the objective function at the final point
-
if the (projected) gradient is available, the value of the largest absolute (projected) gradient element
-
other information specific to the optimization technique
The iteration history generally consists of one line of displayed output containing the most important information for each iteration.
The iteration history always includes the following:
-
the iteration number
-
the number of iteration restarts
-
the number of function calls
-
the number of active constraints
-
the value of the optimization criterion
-
the difference between adjacent function values
-
the maximum of the absolute gradient components that correspond to inactive boundary constraints
An apostrophe trailing the number of active constraints indicates that at least one of the active constraints is released from the active set due to a significant Lagrange multiplier.
For the Levenberg-Marquardt technique (LEVMAR), the iteration history also includes the following information:
-
an asterisk trailing the iteration number when the computed Hessian approximation is singular and consequently ridged with a positive lambda value. If all or the last several iterations show a singular Hessian approximation, the problem is not sufficiently identified. Thus, there are other locally optimal solutions that lead to the same optimum function value for different parameter values. This implies that standard errors for the parameter estimates are not computable without the addition of further constraints.
-
the value of the Lagrange multiplier (lambda). This value is 0 when the optimum of the quadratic function approximation is inside the trust region (a trust-region-scaled Newton step can be performed) and is greater than 0 when the optimum of the quadratic function approximation is located at the boundary of the trust region (the scaled Newton step is too long to fit in the trust region and a quadratic constraint optimization is performed). Large values indicate optimization difficulties. For a nonsingular Hessian matrix, the value of lambda should go to 0 during the last iterations, indicating that the objective function can be well approximated by a quadratic function in a small neighborhood of the optimum point. An increasing lambda value often indicates problems in the optimization process.
-
the value of the ratio
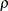 (rho) between the actually achieved difference in function values and the predicted difference in the function values on
the basis of the quadratic function approximation. Values much less than 1 indicate optimization difficulties. The value of
the ratio
(rho) between the actually achieved difference in function values and the predicted difference in the function values on
the basis of the quadratic function approximation. Values much less than 1 indicate optimization difficulties. The value of
the ratio 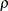 indicates the goodness of the quadratic function approximation. In other words,
indicates the goodness of the quadratic function approximation. In other words, 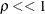 means that the radius of the trust region has to be reduced; a fairly large value of
means that the radius of the trust region has to be reduced; a fairly large value of 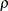 means that the radius of the trust region does not need to be changed. And a value close to or greater than 1 means that
the radius can be increased, indicating a good quadratic function approximation.
means that the radius of the trust region does not need to be changed. And a value close to or greater than 1 means that
the radius can be increased, indicating a good quadratic function approximation.
For the Newton-Raphson technique (NRRIDG), the iteration history also includes the following information:
-
the value of the ridge parameter. This value is 0 when a Newton step can be performed, and it is greater than 0 when either the Hessian approximation is singular or a Newton step fails to reduce the optimization criterion. Large values indicate optimization difficulties.
-
the value of the ratio
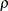 (rho) between the actually achieved difference in function values and the predicted difference in the function values on
the basis of the quadratic function approximation. Values much less than 1.0 indicate optimization difficulties.
(rho) between the actually achieved difference in function values and the predicted difference in the function values on
the basis of the quadratic function approximation. Values much less than 1.0 indicate optimization difficulties.
For the Newton-Raphson with line-search technique (NEWRAP), the iteration history also includes the following information:
-
the step size
 (alpha) computed with one of the line-search algorithms
(alpha) computed with one of the line-search algorithms
-
the slope of the search direction at the current parameter iterate. For minimization, this value should be significantly negative. Otherwise, the line-search algorithm has difficulty reducing the function value sufficiently.
For the trust-region technique (TRUREG), the iteration history also includes the following information:
-
an asterisk after the iteration number when the computed Hessian approximation is singular and consequently ridged with a positive lambda value.
-
the value of the Lagrange multiplier (lambda). This value is zero when the optimum of the quadratic function approximation is inside the trust region (a trust-region-scaled Newton step can be performed) and is greater than zero when the optimum of the quadratic function approximation is located at the boundary of the trust region (the scaled Newton step is too long to fit in the trust region and a quadratically constrained optimization is performed). Large values indicate optimization difficulties. As in Gay (1983), a negative lambda value indicates the special case of an indefinite Hessian matrix (the smallest eigenvalue is negative in minimization).
-
the value of the radius
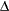 of the trust region. Small trust-region radius values combined with large lambda values in subsequent iterations indicate
optimization problems.
of the trust region. Small trust-region radius values combined with large lambda values in subsequent iterations indicate
optimization problems.
For the quasi-Newton (QUANEW) and conjugate gradient (CONGRA) techniques, the iteration history also includes the following information:
-
the step size (alpha) computed with one of the line-search algorithms
-
the descent of the search direction at the current parameter iterate. This value should be significantly smaller than 0. Otherwise, the line-search algorithm has difficulty reducing the function value sufficiently.
Frequent update restarts (rest) of a quasi-Newton algorithm often indicate numerical problems related to required properties of the approximate Hessian update, and they decrease the speed of convergence. This can happen particularly if the ABSGCONV= termination criterion is too small—that is, when the requested precision cannot be obtained by quasi-Newton optimization. Generally, the number of automatic restarts used by conjugate gradient methods are much higher.
For the nonlinearly constrained quasi-Newton technique, the iteration history also includes the following information:
-
the maximum value of all constraint violations,
![\[ \mbox{conmax} = \max (|c_ i(x)| : c_ i(x) < 0) \]](images/statug_calis0865.png)
-
the value of the predicted function reduction used with the GCONV and FCONV2 termination criteria,
![\[ \mbox{pred} = |g(x^{(k)}) s(x^{(k)})| + \sum _{i=1}^ m |\lambda _ i c_ i(x^{(k)})| \]](images/statug_calis0866.png)
-
the step size
 of the quasi-Newton step. Note that this algorithm works with a special line-search algorithm.
of the quasi-Newton step. Note that this algorithm works with a special line-search algorithm.
-
the maximum element of the gradient of the Lagrange function,
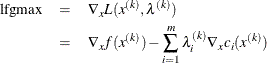
For the double dogleg technique, the iteration history also includes the following information:
-
the parameter
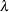 of the double-dogleg step. A value
of the double-dogleg step. A value 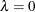 corresponds to the full (quasi) Newton step.
corresponds to the full (quasi) Newton step.
-
the slope of the search direction at the current parameter iterate. For minimization, this value should be significantly negative.
In each iteration k, the (dual) quasi-Newton, hybrid quasi-Newton, conjugate gradient, and Newton-Raphson minimization techniques use iterative
line-search algorithms that try to optimize a linear, quadratic, or cubic approximation of the nonlinear objective function
f of n parameters x along a feasible descent search direction ![]() as follows:
as follows:
by computing an approximately optimal scalar ![]() . Since the outside iteration process is based only on the approximation of the objective function, the inside iteration of
the line-search algorithm does not have to be perfect. Usually, it is satisfactory that the choice of
. Since the outside iteration process is based only on the approximation of the objective function, the inside iteration of
the line-search algorithm does not have to be perfect. Usually, it is satisfactory that the choice of ![]() significantly reduces (in a minimization) the objective function. Criteria often used for termination of line-search algorithms
are the Goldstein conditions (Fletcher, 1987).
significantly reduces (in a minimization) the objective function. Criteria often used for termination of line-search algorithms
are the Goldstein conditions (Fletcher, 1987).
Various line-search algorithms can be selected by using the LIS= option . The line-search methods LIS= 1, LIS= 2, and LIS= 3 satisfy the left-hand-side and right-hand-side Goldstein conditions (Fletcher, 1987).
The line-search method LIS= 2 seems to be superior when function evaluation consumes significantly less computation time than gradient evaluation. Therefore, LIS= 2 is the default value for Newton-Raphson, (dual) quasi-Newton, and conjugate gradient optimizations.
Almost all line-search algorithms use iterative extrapolation techniques that can easily lead to feasible points where the objective function f is no longer defined (resulting in indefinite matrices for ML estimation) or is difficult to compute (resulting in floating point overflows). Therefore, PROC CALIS provides options that restrict the step length or trust region radius, especially during the first main iterations.
The inner product ![]() of the gradient
of the gradient ![]() and the search direction
and the search direction ![]() is the slope of
is the slope of ![]() along the search direction
along the search direction ![]() with step length
with step length ![]() . The default starting value
. The default starting value ![]() in each line-search algorithm (
in each line-search algorithm (![]() ) during the main iteration k is computed in three steps:
) during the main iteration k is computed in three steps:
-
Use either the difference
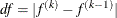 of the function values during the last two consecutive iterations or the final stepsize value
of the function values during the last two consecutive iterations or the final stepsize value 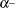 of the previous iteration k – 1 to compute a first value
of the previous iteration k – 1 to compute a first value 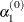 .
.
-
Using the DAMPSTEP<r> option:
![\[ \alpha _1^{(0)} = \min (1,r \alpha ^\_ ) \]](images/statug_calis0880.png)
The initial value for the new step length can be no greater than r times the final step length
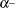 of the previous iteration. The default is r = 2.
of the previous iteration. The default is r = 2.
-
Not using the DAMPSTEP option:
![\[ \alpha _1^{(0)} = \left\{ \begin{array}{ll} \mathit{step} & \mbox{ if $0.1 \le \mathit{step} \le 10$} \\ 10 & \mbox{ if $\mathit{step} > 10 $} \\ 0.1 & \mbox{ if $\mathit{step} < 0.1$} \end{array} \right. \]](images/statug_calis0881.png)
with
![\[ \mathit{step} = \left\{ \begin{array}{ll} \mathit{df} / |\mb{g}^{\prime }\mb{s}| & \mbox{if $ |\mb{g}^{\prime }\mb{s}| \ge \epsilon \max (100 \mathit{df},1)$} \\ 1 & \mbox{otherwise} \end{array} \right. \]](images/statug_calis0882.png)
This value of
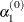 can be too large and can lead to a difficult or impossible function evaluation, especially for highly nonlinear functions
such as the EXP function.
can be too large and can lead to a difficult or impossible function evaluation, especially for highly nonlinear functions
such as the EXP function.
-
-
During the first five iterations, the second step enables you to reduce
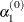 to a smaller starting value
to a smaller starting value 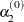 using the INSTEP=
r option:
using the INSTEP=
r option:
![\[ \alpha _2^{(0)} = \min (\alpha _1^{(0)},r) \]](images/statug_calis0884.png)
After more than five iterations,
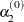 is set to
is set to 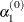 .
.
-
The third step can further reduce the step length by
![\[ \alpha _3^{(0)} = \min (\alpha _2^{(0)},\min (10,u)) \]](images/statug_calis0885.png)
where u is the maximum length of a step inside the feasible region.
The INSTEP=
r option lets you specify a smaller or larger radius of the trust region used in the first iteration by the trust-region, double-dogleg,
and Levenberg-Marquardt algorithms. The default initial trust region radius is the length of the scaled gradient (Moré, 1978). This default length for the initial trust region radius corresponds to the default radius factor of r = 1. This choice is successful in most practical applications of the TRUREG, DBLDOG, and LEVMAR algorithms. However, for
bad initial values used in the analysis of a covariance matrix with high variances or for highly nonlinear constraints (such
as using the EXP function) in your SAS programming statements, the default start radius can result in arithmetic overflows.
If this happens, you can try decreasing values of INSTEP=
r (0 < r < 1), until the iteration starts successfully. A small factor r also affects the trust region radius of the next steps because the radius is changed in each iteration by a factor ![]() depending on the
depending on the ![]() ratio. Reducing the radius corresponds to increasing the ridge parameter
ratio. Reducing the radius corresponds to increasing the ridge parameter ![]() that produces smaller steps directed closer toward the gradient direction.
that produces smaller steps directed closer toward the gradient direction.