The CALIS Procedure
-
Overview

-
Getting Started

-
Syntax
 Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement
Classes of Statements in PROC CALISSingle-Group Analysis SyntaxMultiple-Group Multiple-Model Analysis SyntaxPROC CALIS StatementBOUNDS StatementBY StatementCOSAN StatementCOV StatementDETERM StatementEFFPART StatementFACTOR StatementFITINDEX StatementFREQ StatementGROUP StatementLINCON StatementLINEQS StatementLISMOD StatementLMTESTS StatementMATRIX StatementMEAN StatementMODEL StatementMSTRUCT StatementNLINCON StatementNLOPTIONS StatementOUTFILES StatementPARAMETERS StatementPARTIAL StatementPATH StatementPATHDIAGRAM StatementPCOV StatementPVAR StatementRAM StatementREFMODEL StatementRENAMEPARM StatementSAS Programming StatementsSIMTESTS StatementSTD StatementSTRUCTEQ StatementTESTFUNC StatementVAR StatementVARIANCE StatementVARNAMES StatementWEIGHT Statement -
Details
 Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics
Input Data SetsOutput Data SetsDefault Analysis Type and Default ParameterizationThe COSAN ModelThe FACTOR ModelThe LINEQS ModelThe LISMOD Model and SubmodelsThe MSTRUCT ModelThe PATH ModelThe RAM ModelNaming Variables and ParametersSetting Constraints on ParametersAutomatic Variable SelectionPath Diagrams: Layout Algorithms, Default Settings, and CustomizationEstimation CriteriaRelationships among Estimation CriteriaGradient, Hessian, Information Matrix, and Approximate Standard ErrorsCounting the Degrees of FreedomAssessment of FitCase-Level Residuals, Outliers, Leverage Observations, and Residual DiagnosticsTotal, Direct, and Indirect EffectsStandardized SolutionsModification IndicesMissing Values and the Analysis of Missing PatternsMeasures of Multivariate KurtosisInitial EstimatesUse of Optimization TechniquesComputational ProblemsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis
Estimating Covariances and CorrelationsEstimating Covariances and Means SimultaneouslyTesting Uncorrelatedness of VariablesTesting Covariance PatternsTesting Some Standard Covariance Pattern HypothesesLinear Regression ModelMultivariate Regression ModelsMeasurement Error ModelsTesting Specific Measurement Error ModelsMeasurement Error Models with Multiple PredictorsMeasurement Error Models Specified As Linear EquationsConfirmatory Factor ModelsConfirmatory Factor Models: Some VariationsResidual Diagnostics and Robust EstimationThe Full Information Maximum Likelihood MethodComparing the ML and FIML EstimationPath Analysis: Stability of AlienationSimultaneous Equations with Mean Structures and Reciprocal PathsFitting Direct Covariance StructuresConfirmatory Factor Analysis: Cognitive AbilitiesTesting Equality of Two Covariance Matrices Using a Multiple-Group AnalysisTesting Equality of Covariance and Mean Matrices between Independent GroupsIllustrating Various General Modeling LanguagesTesting Competing Path Models for the Career Aspiration DataFitting a Latent Growth Curve ModelHigher-Order and Hierarchical Factor ModelsLinear Relations among Factor LoadingsMultiple-Group Model for Purchasing BehaviorFitting the RAM and EQS Models by the COSAN Modeling LanguageSecond-Order Confirmatory Factor AnalysisLinear Relations among Factor Loadings: COSAN Model SpecificationOrdinal Relations among Factor LoadingsLongitudinal Factor Analysis - References
In many applications, the manifest variables are not even approximately multivariate normal. If this happens to be the case with your data set, the default generalized least squares and maximum likelihood estimation methods are not appropriate, and you should compute the parameter estimates and their standard errors by an asymptotically distribution-free method, such as the WLS estimation method. If your manifest variables are multivariate normal, then they have a zero relative multivariate kurtosis, and all marginal distributions have zero kurtosis (Browne, 1982). If your DATA= data set contains raw data, PROC CALIS computes univariate skewness and kurtosis and a set of multivariate kurtosis values. By default, the values of univariate skewness and kurtosis are corrected for bias (as in PROC UNIVARIATE), but using the BIASKUR option enables you to compute the uncorrected values also. The values are displayed when you specify the PROC CALIS statement option KURTOSIS .
In the following formulas, N denotes the sample size and p denotes the number of variables.
-
corrected variance for variable
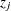
![\[ \sigma _ j^2 = \frac{1}{N-1} {\sum _ i^ N(z_{ij} - \bar{z}_ j)^2} \]](images/statug_calis0831.png)
-
uncorrected univariate skewness for variable
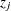
![\[ \gamma _{1(j)} = \frac{ {N \sum _ i^ N (z_{ij} - \bar{z}_ j)^3}}{\sqrt {N [\sum _ i^ N (z_{ij} - \bar{z}_ j)^2]^3 } } \]](images/statug_calis0832.png)
-
corrected univariate skewness for variable
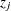
![\[ \gamma _{1(j)} = \frac{N}{(N - 1)(N - 2)} \frac{{\sum _ i^ N (z_{ij} - \bar{z}_ j)^3}}{\sigma _ j^3} \]](images/statug_calis0833.png)
-
uncorrected univariate kurtosis for variable
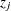
![\[ \gamma _{2(j)} = \frac{ N {\sum _ i^ N (z_{ij} - \bar{z}_ j)^4}}{[\sum _ i^ N (z_{ij} - \bar{z}_ j)^2]^2 } - 3 \]](images/statug_calis0834.png)
-
corrected univariate kurtosis for variable
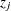
![\[ \gamma _{2(j)} = \frac{N(N + 1)}{(N - 1)(N - 2)(N - 3)} \frac{ {\sum _ i^ N (z_{ij} - \bar{z}_ j)^4}}{\sigma _ j^4} - \frac{3(N - 1)^2}{(N - 2)(N - 3)} \]](images/statug_calis0835.png)
-
Mardia’s multivariate kurtosis
![\[ \gamma _2 = {\frac{1}{N} {\sum _ i^ N[(z_ i - \bar{z})^{\prime } \mb{S}^{-1} (z_ i - \bar{z})]^2} - p(p + 2) } \]](images/statug_calis0836.png)
where
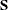 is the biased sample covariance matrix with N as the divisor.
is the biased sample covariance matrix with N as the divisor.
-
relative multivariate kurtosis
![\[ \eta _2 = \frac{ {\gamma _2 + p(p + 2)}}{ {p(p + 2)} } \]](images/statug_calis0837.png)
-
normalized multivariate kurtosis
![\[ \kappa _0 = \frac{ \gamma _2 }{\sqrt {8p(p + 2) / N} } \]](images/statug_calis0838.png)
-
Mardia based kappa
![\[ \kappa _1 = \frac{\gamma _2}{p(p + 2) } \]](images/statug_calis0839.png)
-
mean scaled univariate kurtosis
![\[ \kappa _2 = { \frac{1}{3p} {\sum _ j^ p \gamma _{2(j)}} } \]](images/statug_calis0840.png)
-
adjusted mean scaled univariate kurtosis
![\[ \kappa _3 = { \frac{1}{3p} {\sum _ j^ p \gamma ^*_{2(j)}} } \]](images/statug_calis0841.png)
with
![\[ \gamma ^*_{2(j)} = \left\{ \begin{matrix} \gamma _{2(j)} \quad , & \quad \mbox{if} \quad \gamma _{2(j)} > \frac{-6}{p+2} \\ \frac{-6}{p+2} \quad , & \mbox{otherwise} \\ \end{matrix} \right. \]](images/statug_calis0842.png)
If variable ![]() is normally distributed, the uncorrected univariate kurtosis
is normally distributed, the uncorrected univariate kurtosis ![]() is equal to 0. If Z has an p-variate normal distribution, Mardia’s multivariate kurtosis
is equal to 0. If Z has an p-variate normal distribution, Mardia’s multivariate kurtosis ![]() is equal to 0. A variable
is equal to 0. A variable ![]() is called leptokurtic if it has a positive value of
is called leptokurtic if it has a positive value of ![]() and is called platykurtic if it has a negative value of
and is called platykurtic if it has a negative value of ![]() . The values of
. The values of ![]() ,
, ![]() , and
, and ![]() should not be smaller than the following lower bound (Bentler, 1985):
should not be smaller than the following lower bound (Bentler, 1985):
PROC CALIS displays a message if ![]() ,
, ![]() , or
, or ![]() falls below the lower bound.
falls below the lower bound.
If weighted least squares estimates (METHOD= WLS or METHOD= ADF) are specified and the weight matrix is computed from an input raw data set, the CALIS procedure computes two more measures of multivariate kurtosis.
The occurrence of significant nonzero values of Mardia’s multivariate kurtosis ![]() and significant amounts of some of the univariate kurtosis values
and significant amounts of some of the univariate kurtosis values ![]() indicate that your variables are not multivariate normal distributed. Violating the multivariate normality assumption in
(default) generalized least squares and maximum likelihood estimation usually leads to the wrong approximate standard errors
and incorrect fit statistics based on the
indicate that your variables are not multivariate normal distributed. Violating the multivariate normality assumption in
(default) generalized least squares and maximum likelihood estimation usually leads to the wrong approximate standard errors
and incorrect fit statistics based on the ![]() value. In general, the parameter estimates are more stable against violation of the normal distribution assumption. For more
details, see Browne (1974, 1982, 1984).
value. In general, the parameter estimates are more stable against violation of the normal distribution assumption. For more
details, see Browne (1974, 1982, 1984).