The GLM Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Statistical Assumptions for Using PROC GLM Specification of Effects Using PROC GLM Interactively Parameterization of PROC GLM Models Hypothesis Testing in PROC GLM Effect Size Measures for F Tests in GLM Absorption Specification of ESTIMATE Expressions Comparing Groups Multivariate Analysis of Variance Repeated Measures Analysis of Variance Random-Effects Analysis Missing Values Computational Resources Computational Method Output Data Sets Displayed Output ODS Table Names ODS Graphics
Statistical Assumptions for Using PROC GLM Specification of Effects Using PROC GLM Interactively Parameterization of PROC GLM Models Hypothesis Testing in PROC GLM Effect Size Measures for F Tests in GLM Absorption Specification of ESTIMATE Expressions Comparing Groups Multivariate Analysis of Variance Repeated Measures Analysis of Variance Random-Effects Analysis Missing Values Computational Resources Computational Method Output Data Sets Displayed Output ODS Table Names ODS Graphics -
Examples
 Randomized Complete Blocks with Means Comparisons and Contrasts Regression with Mileage Data Unbalanced ANOVA for Two-Way Design with Interaction Analysis of Covariance Three-Way Analysis of Variance with Contrasts Multivariate Analysis of Variance Repeated Measures Analysis of Variance Mixed Model Analysis of Variance with the RANDOM Statement Analyzing a Doubly Multivariate Repeated Measures Design Testing for Equal Group Variances Analysis of a Screening Design
Randomized Complete Blocks with Means Comparisons and Contrasts Regression with Mileage Data Unbalanced ANOVA for Two-Way Design with Interaction Analysis of Covariance Three-Way Analysis of Variance with Contrasts Multivariate Analysis of Variance Repeated Measures Analysis of Variance Mixed Model Analysis of Variance with the RANDOM Statement Analyzing a Doubly Multivariate Repeated Measures Design Testing for Equal Group Variances Analysis of a Screening Design - References
Example 41.11 Analysis of a Screening Design
Yin and Jillie (1987) describe an experiment performed on a nitride etch process for a single wafer plasma etcher. The experiment is run using four factors: cathode power (power), gas flow (flow), reactor chamber pressure (pressure), and electrode gap (gap). Of interest are the main effects and interaction effects of the factors on the nitride etch rate (rate). The following statements create a SAS data set named HalfFraction, containing the factor settings and the observed etch rate for each of eight experimental runs.
data HalfFraction; input power flow pressure gap rate; datalines; 0.8 4.5 125 275 550 0.8 4.5 200 325 650 0.8 550.0 125 325 642 0.8 550.0 200 275 601 1.2 4.5 125 325 749 1.2 4.5 200 275 1052 1.2 550.0 125 275 1075 1.2 550.0 200 325 729 ;
Notice that each of the factors has just two values. This is a common experimental design when the intent is to screen from the many factors that might affect the response the few that actually do. Since there are 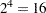 different possible settings of four two-level factors, this design with only eight runs is called a "half fraction." The eight runs are chosen specifically to provide unambiguous information on main effects at the cost of confounding interaction effects with each other.
different possible settings of four two-level factors, this design with only eight runs is called a "half fraction." The eight runs are chosen specifically to provide unambiguous information on main effects at the cost of confounding interaction effects with each other.
One way to analyze these data is simply to use PROC GLM to compute an analysis of variance, including both main effects and interactions in the model. The following statements demonstrate this approach.
proc glm data=HalfFraction; class power flow pressure gap; model rate=power|flow|pressure|gap@2; run;
The "@2" notation in the MODEL statement includes all main effects and two-factor interactions between the factors. The output is shown in Output 41.11.1.
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| power | 2 | 0.8 1.2 |
| flow | 2 | 4.5 550 |
| pressure | 2 | 125 200 |
| gap | 2 | 275 325 |
| Number of Observations Read | 8 |
|---|---|
| Number of Observations Used | 8 |
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 7 | 280848.0000 | 40121.1429 | . | . |
| Error | 0 | 0.0000 | . | ||
| Corrected Total | 7 | 280848.0000 |
| R-Square | Coeff Var | Root MSE | rate Mean |
|---|---|---|---|
| 1.000000 | . | . | 756.0000 |
| Source | DF | Type I SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| power | 1 | 168780.5000 | 168780.5000 | . | . |
| flow | 1 | 264.5000 | 264.5000 | . | . |
| power*flow | 1 | 200.0000 | 200.0000 | . | . |
| pressure | 1 | 32.0000 | 32.0000 | . | . |
| power*pressure | 1 | 1300.5000 | 1300.5000 | . | . |
| flow*pressure | 1 | 78012.5000 | 78012.5000 | . | . |
| gap | 1 | 32258.0000 | 32258.0000 | . | . |
| power*gap | 0 | 0.0000 | . | . | . |
| flow*gap | 0 | 0.0000 | . | . | . |
| pressure*gap | 0 | 0.0000 | . | . | . |
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| power | 1 | 168780.5000 | 168780.5000 | . | . |
| flow | 1 | 264.5000 | 264.5000 | . | . |
| power*flow | 0 | 0.0000 | . | . | . |
| pressure | 1 | 32.0000 | 32.0000 | . | . |
| power*pressure | 0 | 0.0000 | . | . | . |
| flow*pressure | 0 | 0.0000 | . | . | . |
| gap | 1 | 32258.0000 | 32258.0000 | . | . |
| power*gap | 0 | 0.0000 | . | . | . |
| flow*gap | 0 | 0.0000 | . | . | . |
| pressure*gap | 0 | 0.0000 | . | . | . |
Notice that there are no error degrees of freedom. This is because there are 10 effects in the model (4 main effects plus 6 interactions) but only 8 observations in the data set. This is another cost of using a fractional design: not only is it impossible to estimate all the main effects and interactions, but there is also no information left to estimate the underlying error rate in order to measure the significance of the effects that are estimable.
Another thing to notice in Output 41.11.1 is the difference between the Type I and Type III ANOVA tables. The rows corresponding to main effects in each are the same, but no Type III interaction tests are estimable, while some Type I interaction tests are estimable. This indicates that there is aliasing in the design: some interactions are completely confounded with each other.
In order to analyze this confounding, you should examine the aliasing structure of the design by using the ALIASING option in the MODEL statement. Before doing so, however, it is advisable to code the design, replacing low and high levels of each factor with the values 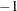 and
and 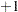 , respectively. This puts each factor on an equal footing in the model and makes the aliasing structure much more interpretable. The following statements code the data, creating a new data set named Coded.
, respectively. This puts each factor on an equal footing in the model and makes the aliasing structure much more interpretable. The following statements code the data, creating a new data set named Coded.
data Coded; set HalfFraction; power = -1*(power =0.80) + 1*(power =1.20); flow = -1*(flow =4.50) + 1*(flow =550 ); pressure = -1*(pressure=125 ) + 1*(pressure=200 ); gap = -1*(gap =275 ) + 1*(gap =325 ); run;
The following statements use the GLM procedure to reanalyze the coded design, displaying the parameter estimates as well as the functions of the parameters that they each estimate.
proc glm data=Coded; model rate=power|flow|pressure|gap@2 / solution aliasing; run;
The parameter estimates table is shown in Output 41.11.2.
| Parameter | Estimate | Standard Error | t Value | Pr > |t| | Expected Value | |
|---|---|---|---|---|---|---|
| Intercept | 756.0000000 | . | . | . | Intercept | |
| power | 145.2500000 | . | . | . | power | |
| flow | 5.7500000 | . | . | . | flow | |
| power*flow | -5.0000000 | B | . | . | . | power*flow + pressure*gap |
| pressure | 2.0000000 | . | . | . | pressure | |
| power*pressure | -12.7500000 | B | . | . | . | power*pressure + flow*gap |
| flow*pressure | -98.7500000 | B | . | . | . | flow*pressure + power*gap |
| gap | -63.5000000 | . | . | . | gap | |
| power*gap | 0.0000000 | B | . | . | . | |
| flow*gap | 0.0000000 | B | . | . | . | |
| pressure*gap | 0.0000000 | B | . | . | . |
In the "Expected Value" column, notice that, while each of the main effects is unambiguously estimated by its associated term in the model, the expected values of the interaction estimates are more complicated. For example, the relatively large effect (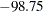 ) corresponding to flow*pressure actually estimates the combined effect of flow*pressure and power*gap. Without further information, it is impossible to disentangle these aliased interactions; however, since the main effects of both power and gap are large and those for flow and pressure are small, it is reasonable to suspect that power*gap is the more "active" of the two interactions.
) corresponding to flow*pressure actually estimates the combined effect of flow*pressure and power*gap. Without further information, it is impossible to disentangle these aliased interactions; however, since the main effects of both power and gap are large and those for flow and pressure are small, it is reasonable to suspect that power*gap is the more "active" of the two interactions.
Fortunately, eight more runs are available for this experiment (the other half fraction). The following statements create a data set containing these extra runs and add it to the previous eight, resulting in a full 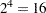 run replicate. Then PROC GLM displays the analysis of variance again.
run replicate. Then PROC GLM displays the analysis of variance again.
data OtherHalf; input power flow pressure gap rate; datalines; 0.8 4.5 125 325 669 0.8 4.5 200 275 604 0.8 550.0 125 275 633 0.8 550.0 200 325 635 1.2 4.5 125 275 1037 1.2 4.5 200 325 868 1.2 550.0 125 325 860 1.2 550.0 200 275 1063 ; data FullRep; set HalfFraction OtherHalf; run;
proc glm data=FullRep; class power flow pressure gap; model rate=power|flow|pressure|gap@2; run;
The results are displayed in Output 41.11.3.
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| power | 2 | 0.8 1.2 |
| flow | 2 | 4.5 550 |
| pressure | 2 | 125 200 |
| gap | 2 | 275 325 |
| Number of Observations Read | 16 |
|---|---|
| Number of Observations Used | 16 |
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 10 | 521234.1250 | 52123.4125 | 25.58 | 0.0011 |
| Error | 5 | 10186.8125 | 2037.3625 | ||
| Corrected Total | 15 | 531420.9375 |
| R-Square | Coeff Var | Root MSE | rate Mean |
|---|---|---|---|
| 0.980831 | 5.816175 | 45.13715 | 776.0625 |
| Source | DF | Type I SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| power | 1 | 374850.0625 | 374850.0625 | 183.99 | <.0001 |
| flow | 1 | 217.5625 | 217.5625 | 0.11 | 0.7571 |
| power*flow | 1 | 18.0625 | 18.0625 | 0.01 | 0.9286 |
| pressure | 1 | 10.5625 | 10.5625 | 0.01 | 0.9454 |
| power*pressure | 1 | 1.5625 | 1.5625 | 0.00 | 0.9790 |
| flow*pressure | 1 | 7700.0625 | 7700.0625 | 3.78 | 0.1095 |
| gap | 1 | 41310.5625 | 41310.5625 | 20.28 | 0.0064 |
| power*gap | 1 | 94402.5625 | 94402.5625 | 46.34 | 0.0010 |
| flow*gap | 1 | 2475.0625 | 2475.0625 | 1.21 | 0.3206 |
| pressure*gap | 1 | 248.0625 | 248.0625 | 0.12 | 0.7414 |
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| power | 1 | 374850.0625 | 374850.0625 | 183.99 | <.0001 |
| flow | 1 | 217.5625 | 217.5625 | 0.11 | 0.7571 |
| power*flow | 1 | 18.0625 | 18.0625 | 0.01 | 0.9286 |
| pressure | 1 | 10.5625 | 10.5625 | 0.01 | 0.9454 |
| power*pressure | 1 | 1.5625 | 1.5625 | 0.00 | 0.9790 |
| flow*pressure | 1 | 7700.0625 | 7700.0625 | 3.78 | 0.1095 |
| gap | 1 | 41310.5625 | 41310.5625 | 20.28 | 0.0064 |
| power*gap | 1 | 94402.5625 | 94402.5625 | 46.34 | 0.0010 |
| flow*gap | 1 | 2475.0625 | 2475.0625 | 1.21 | 0.3206 |
| pressure*gap | 1 | 248.0625 | 248.0625 | 0.12 | 0.7414 |
With 16 runs, the analysis of variance tells the whole story: all effects are estimable and there are five degrees of freedom left over to estimate the underlying error. The main effects of power and gap and their interaction are all significant, and no other effects are. Notice that the Type I and Type III ANOVA tables are the same; this is because the design is orthogonal and all effects are estimable.
This example illustrates the use of the GLM procedure for the model analysis of a screening experiment. Typically, there is much more involved in performing an experiment of this type, from selecting the design points to be studied to graphically assessing significant effects, optimizing the final model, and performing subsequent experimentation. Specialized tools for this are available in SAS/QC software, in particular the ADX Interface and the FACTEX and OPTEX procedures. See SAS/QC User’s Guide for more information.