The GLM Procedure
-
Overview
-
Getting Started
-
Syntax
-
Details
Statistical Assumptions for Using PROC GLM Specification of Effects Using PROC GLM Interactively Parameterization of PROC GLM Models Hypothesis Testing in PROC GLM Effect Size Measures for F Tests in GLM Absorption Specification of ESTIMATE Expressions Comparing Groups Multivariate Analysis of Variance Repeated Measures Analysis of Variance Random-Effects Analysis Missing Values Computational Resources Computational Method Output Data Sets Displayed Output ODS Table Names ODS Graphics
-
Examples
Randomized Complete Blocks with Means Comparisons and Contrasts Regression with Mileage Data Unbalanced ANOVA for Two-Way Design with Interaction Analysis of Covariance Three-Way Analysis of Variance with Contrasts Multivariate Analysis of Variance Repeated Measures Analysis of Variance Mixed Model Analysis of Variance with the RANDOM Statement Analyzing a Doubly Multivariate Repeated Measures Design Testing for Equal Group Variances Analysis of a Screening Design
- References
| Displayed Output |
The GLM procedure produces the following output by default:
The overall analysis-of-variance table breaks down the Total Sum of Squares for the dependent variable into the portion attributed to the Model and the portion attributed to Error.
The Mean Square term is the Sum of Squares divided by the degrees of freedom (DF).
The Mean Square for Error is an estimate of
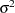, the variance of the true errors. The
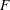Value is the ratio produced by dividing the Mean Square for the Model by the Mean Square for Error. It tests how well the model as a whole (adjusted for the mean) accounts for the dependent variable’s behavior. An 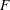test is a joint test to determine that all parameters except the intercept are zero. A small significance probability, Pr > F, indicates that some linear function of the parameters is significantly different from zero.
R-Square,
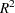, measures how much variation in the dependent variable can be accounted for by the model. 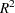, which can range from 0 to 1, is the ratio of the sum of squares for the model to the corrected total sum of squares. In general, the larger the value of 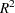, the better the model’s fit. Coeff Var, the coefficient of variation, which describes the amount of variation in the population, is 100 times the standard deviation estimate of the dependent variable, Root MSE (Mean Square for Error), divided by the Mean. The coefficient of variation is often a preferred measure because it is unitless.
Root MSE estimates the standard deviation of the dependent variable (or equivalently, the error term) and equals the square root of the Mean Square for Error.
Mean is the sample mean of the dependent variable.
These tests are used primarily in analysis-of-variance applications:
The Type I SS (sum of squares) measures incremental sums of squares for the model as each variable is added.
The Type III SS is the sum of squares for a balanced test of each effect, adjusted for every other effect.
These items are used primarily in regression applications:
The Estimates for the model Parameters (the intercept and the coefficients)
t Value is the Student’s
value for testing the null hypothesis that the parameter (if it is estimable) equals zero. The significance level, Pr > |t|, is the probability of getting a larger value of
if the parameter is truly equal to zero. A very small value for this probability leads to the conclusion that the independent variable contributes significantly to the model. The Standard Error is the square root of the estimated variance of the estimate of the true value of the parameter.
Other portions of output are discussed in the following examples.