The GLM Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Statistical Assumptions for Using PROC GLM Specification of Effects Using PROC GLM Interactively Parameterization of PROC GLM Models Hypothesis Testing in PROC GLM Effect Size Measures for F Tests in GLM Absorption Specification of ESTIMATE Expressions Comparing Groups Multivariate Analysis of Variance Repeated Measures Analysis of Variance Random-Effects Analysis Missing Values Computational Resources Computational Method Output Data Sets Displayed Output ODS Table Names ODS Graphics
Statistical Assumptions for Using PROC GLM Specification of Effects Using PROC GLM Interactively Parameterization of PROC GLM Models Hypothesis Testing in PROC GLM Effect Size Measures for F Tests in GLM Absorption Specification of ESTIMATE Expressions Comparing Groups Multivariate Analysis of Variance Repeated Measures Analysis of Variance Random-Effects Analysis Missing Values Computational Resources Computational Method Output Data Sets Displayed Output ODS Table Names ODS Graphics -
Examples
 Randomized Complete Blocks with Means Comparisons and Contrasts Regression with Mileage Data Unbalanced ANOVA for Two-Way Design with Interaction Analysis of Covariance Three-Way Analysis of Variance with Contrasts Multivariate Analysis of Variance Repeated Measures Analysis of Variance Mixed Model Analysis of Variance with the RANDOM Statement Analyzing a Doubly Multivariate Repeated Measures Design Testing for Equal Group Variances Analysis of a Screening Design
Randomized Complete Blocks with Means Comparisons and Contrasts Regression with Mileage Data Unbalanced ANOVA for Two-Way Design with Interaction Analysis of Covariance Three-Way Analysis of Variance with Contrasts Multivariate Analysis of Variance Repeated Measures Analysis of Variance Mixed Model Analysis of Variance with the RANDOM Statement Analyzing a Doubly Multivariate Repeated Measures Design Testing for Equal Group Variances Analysis of a Screening Design - References
| REPEATED Statement |
- REPEATED factor-specification </ options> ;
When values of the dependent variables in the MODEL statement represent repeated measurements on the same experimental unit, the REPEATED statement enables you to test hypotheses about the measurement factors (often called within-subject factors) as well as the interactions of within-subject factors with independent variables in the MODEL statement (often called between-subject factors). The REPEATED statement provides multivariate and univariate tests as well as hypothesis tests for a variety of single-degree-of-freedom contrasts. There is no limit to the number of within-subject factors that can be specified.
The REPEATED statement is typically used for handling repeated measures designs with one repeated response variable. Usually, the variables on the left-hand side of the equation in the MODEL statement represent one repeated response variable. This does not mean that only one factor can be listed in the REPEATED statement. For example, one repeated response variable (hemoglobin count) might be measured 12 times (implying variables Y1 to Y12 on the left-hand side of the equal sign in the MODEL statement), with the associated within-subject factors treatment and time (implying two factors listed in the REPEATED statement). See the section Examples for an example of how PROC GLM handles this case.
Designs with two or more repeated response variables can, however, be handled with the IDENTITY transformation; see the description of this transformation in the following section, and see Example 41.9 for an example of analyzing a doubly multivariate repeated measures design.
When a REPEATED statement appears, the GLM procedure enters a multivariate mode of handling missing values. If any values for variables corresponding to each combination of the within-subject factors are missing, the observation is excluded from the analysis.
If you use a CONTRAST or TEST statement with a REPEATED statement, you must enter the CONTRAST or TEST statement before the REPEATED statement.
The simplest form of the REPEATED statement requires only a factor-name. With two repeated factors, you must specify the factor-name and number of levels (levels) for each factor. Optionally, you can specify the actual values for the levels (level-values), a transformation that defines single-degree-of-freedom contrasts, and options for additional analyses and output. When you specify more than one within-subject factor, the factor-names (and associated level and transformation information) must be separated by a comma in the REPEATED statement.
These terms are described in the following section, "Syntax Details."
Syntax Details
You can specify the following terms in the REPEATED statement.
- factor-specification
-
The factor-specification for the REPEATED statement can include any number of individual factor specifications, separated by commas, of the following form:
factor-name levels < (level-values) > < transformation >
where
- factor-name
-
names a factor to be associated with the dependent variables. The name should not be the same as any variable name that already exists in the data set being analyzed and should conform to the usual conventions of SAS variable names.
When specifying more than one factor, list the dependent variables in the MODEL statement so that the within-subject factors defined in the REPEATED statement are nested; that is, the first factor defined in the REPEATED statement should be the one with values that change least frequently.
- levels
gives the number of levels associated with the factor being defined. When there is only one within-subject factor, the number of levels is equal to the number of dependent variables. In this case, levels is optional. When more than one within-subject factor is defined, however, levels is required, and the product of the number of levels of all the factors must equal the number of dependent variables in the MODEL statement.
- (level-values)
gives values that correspond to levels of a repeated-measures factor. These values are used to label output and as spacings for constructing orthogonal polynomial contrasts if you specify a POLYNOMIAL transformation. The number of values specified must correspond to the number of levels for that factor in the REPEATED statement. Enclose the level-values in parentheses.
The following transformation keywords define single-degree-of-freedom contrasts for factors specified in the REPEATED statement. Since the number of contrasts generated is always one less than the number of levels of the factor, you have some control over which contrast is omitted from the analysis by which transformation you select. The only exception is the IDENTITY transformation; this transformation is not composed of contrasts and has the same degrees of freedom as the factor has levels. By default, the procedure uses the CONTRAST transformation.
- CONTRAST<(ordinal-reference-level)>
-
generates contrasts between levels of the factor and a reference level. By default, the procedure uses the last level as the reference level; you can optionally specify a reference level in parentheses after the keyword CONTRAST. The reference level corresponds to the ordinal value of the level rather than the level value specified. For example, to generate contrasts between the first level of a factor and the other levels, use
contrast(1)
- HELMERT
generates contrasts between each level of the factor and the mean of subsequent levels.
- IDENTITY
generates an identity transformation corresponding to the associated factor. This transformation is not composed of contrasts; it has
 degrees of freedom for an
degrees of freedom for an  -level factor, instead of
-level factor, instead of 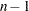 . This can be used for doubly multivariate repeated measures.
. This can be used for doubly multivariate repeated measures. - MEAN<(ordinal-reference-level)>
generates contrasts between levels of the factor and the mean of all other levels of the factor. Specifying a reference level eliminates the contrast between that level and the mean. Without a reference level, the contrast involving the last level is omitted. See the CONTRAST transformation for an example.
- POLYNOMIAL
generates orthogonal polynomial contrasts. Level values, if provided, are used as spacings in the construction of the polynomials; otherwise, equal spacing is assumed.
- PROFILE
You can specify the following options in the REPEATED statement after a slash (/).
- CANONICAL
performs a canonical analysis of the
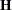 and
and 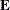 matrices corresponding to the transformed variables specified in the REPEATED statement.
matrices corresponding to the transformed variables specified in the REPEATED statement. - HTYPE=n
specifies the type of the
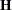 matrix used in the multivariate tests and the type of sums of squares used in the univariate tests. See the HTYPE= option in the specifications for the MANOVA statement for further details.
matrix used in the multivariate tests and the type of sums of squares used in the univariate tests. See the HTYPE= option in the specifications for the MANOVA statement for further details. - MEAN
generates the overall arithmetic means of the within-subject variables.
- MSTAT=FAPPROX | EXACT
specifies the method of evaluating the test statistics for the multivariate analysis. The default is MSTAT=FAPPROX, which specifies that the multivariate tests are evaluated using the usual approximations based on the
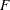 distribution, as discussed in the section "Multivariate Tests" in
Chapter 4,
Introduction to Regression Procedures.
Alternatively, you can specify MSTAT=EXACT to compute exact p-values for three of the four tests (Wilks’ lambda, the Hotelling-Lawley trace, and Roy’s greatest root) and an improved
distribution, as discussed in the section "Multivariate Tests" in
Chapter 4,
Introduction to Regression Procedures.
Alternatively, you can specify MSTAT=EXACT to compute exact p-values for three of the four tests (Wilks’ lambda, the Hotelling-Lawley trace, and Roy’s greatest root) and an improved 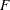 approximation for the fourth (Pillai’s trace). While MSTAT=EXACT provides better control of the significance probability for the tests, especially for Roy’s greatest root, computations for the exact p-values can be appreciably more demanding, and are in fact infeasible for large problems (many dependent variables). Thus, although MSTAT=EXACT is more accurate for most data, it is not the default method. For more information about the results of MSTAT=EXACT, see the section Multivariate Analysis of Variance.
approximation for the fourth (Pillai’s trace). While MSTAT=EXACT provides better control of the significance probability for the tests, especially for Roy’s greatest root, computations for the exact p-values can be appreciably more demanding, and are in fact infeasible for large problems (many dependent variables). Thus, although MSTAT=EXACT is more accurate for most data, it is not the default method. For more information about the results of MSTAT=EXACT, see the section Multivariate Analysis of Variance. - NOM
- NOU
- PRINTE
displays the
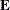 matrix for each combination of within-subject factors, as well as partial correlation matrices for both the original dependent variables and the variables defined by the transformations specified in the REPEATED statement. In addition, the PRINTE option provides sphericity tests for each set of transformed variables. If the requested transformations are not orthogonal, the PRINTE option also provides a sphericity test for a set of orthogonal contrasts.
matrix for each combination of within-subject factors, as well as partial correlation matrices for both the original dependent variables and the variables defined by the transformations specified in the REPEATED statement. In addition, the PRINTE option provides sphericity tests for each set of transformed variables. If the requested transformations are not orthogonal, the PRINTE option also provides a sphericity test for a set of orthogonal contrasts. - PRINTH
displays the
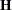 (SSCP) matrix associated with each multivariate test.
(SSCP) matrix associated with each multivariate test. - PRINTM
-
displays the transformation matrices that define the contrasts in the analysis. PROC GLM always displays the
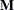 matrix so that the transformed variables are defined by the rows, not the columns, of the displayed
matrix so that the transformed variables are defined by the rows, not the columns, of the displayed 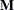 matrix. In other words, PROC GLM actually displays
matrix. In other words, PROC GLM actually displays 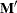 .
. - PRINTRV
displays the characteristic roots and vectors for each multivariate test.
- SUMMARY
produces analysis-of-variance tables for each contrast defined by the within-subject factors. Along with tests for the effects of the independent variables specified in the MODEL statement, a term labeled MEAN tests the hypothesis that the overall mean of the contrast is zero.
- UEPSDEF=unbiased-epsilon-definition
specifies the type of adjustment for the univariate
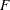 test that is displayed in addition to the Greenhouse-Geisser adjustment. The default is UEPSDEF=HFL, corresponding to the corrected form of the Huynh-Feldt adjustment (Huynh and Feldt; 1976; Lecoutre; 1991). Other alternatives are UEPSDEF=HF, the uncorrected Huynh-Feldt adjustment (the only available method in previous releases of SAS/STAT software), and UEPSDEF=CM, the adjustment of Chi and Muller (2009). See the section Hypothesis Testing in Repeated Measures Analysis for details about these adjustments.
test that is displayed in addition to the Greenhouse-Geisser adjustment. The default is UEPSDEF=HFL, corresponding to the corrected form of the Huynh-Feldt adjustment (Huynh and Feldt; 1976; Lecoutre; 1991). Other alternatives are UEPSDEF=HF, the uncorrected Huynh-Feldt adjustment (the only available method in previous releases of SAS/STAT software), and UEPSDEF=CM, the adjustment of Chi and Muller (2009). See the section Hypothesis Testing in Repeated Measures Analysis for details about these adjustments.
Examples
When specifying more than one factor, list the dependent variables in the MODEL statement so that the within-subject factors defined in the REPEATED statement are nested; that is, the first factor defined in the REPEATED statement should be the one with values that change least frequently. For example, assume that three treatments are administered at each of four times, for a total of twelve dependent variables on each experimental unit. If the variables are listed in the MODEL statement as Y1 through Y12, then the REPEATED statement in
proc glm;
classes group;
model Y1-Y12=group / nouni;
repeated trt 3, time 4;
run;
implies the following structure:
Dependent Variables |
||||||||||||
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
Y7 |
Y8 |
Y9 |
Y10 |
Y11 |
Y12 |
|
Value of trt |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
Value of time |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
The REPEATED statement always produces a table like the preceding one. For more information, see the section Repeated Measures Analysis of Variance.