The GLM Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Statistical Assumptions for Using PROC GLM Specification of Effects Using PROC GLM Interactively Parameterization of PROC GLM Models Hypothesis Testing in PROC GLM Effect Size Measures for F Tests in GLM Absorption Specification of ESTIMATE Expressions Comparing Groups Multivariate Analysis of Variance Repeated Measures Analysis of Variance Random-Effects Analysis Missing Values Computational Resources Computational Method Output Data Sets Displayed Output ODS Table Names ODS Graphics
Statistical Assumptions for Using PROC GLM Specification of Effects Using PROC GLM Interactively Parameterization of PROC GLM Models Hypothesis Testing in PROC GLM Effect Size Measures for F Tests in GLM Absorption Specification of ESTIMATE Expressions Comparing Groups Multivariate Analysis of Variance Repeated Measures Analysis of Variance Random-Effects Analysis Missing Values Computational Resources Computational Method Output Data Sets Displayed Output ODS Table Names ODS Graphics -
Examples
 Randomized Complete Blocks with Means Comparisons and Contrasts Regression with Mileage Data Unbalanced ANOVA for Two-Way Design with Interaction Analysis of Covariance Three-Way Analysis of Variance with Contrasts Multivariate Analysis of Variance Repeated Measures Analysis of Variance Mixed Model Analysis of Variance with the RANDOM Statement Analyzing a Doubly Multivariate Repeated Measures Design Testing for Equal Group Variances Analysis of a Screening Design
Randomized Complete Blocks with Means Comparisons and Contrasts Regression with Mileage Data Unbalanced ANOVA for Two-Way Design with Interaction Analysis of Covariance Three-Way Analysis of Variance with Contrasts Multivariate Analysis of Variance Repeated Measures Analysis of Variance Mixed Model Analysis of Variance with the RANDOM Statement Analyzing a Doubly Multivariate Repeated Measures Design Testing for Equal Group Variances Analysis of a Screening Design - References
Example 41.7 Repeated Measures Analysis of Variance
This example uses data from Cole and Grizzle (1966) to illustrate a commonly occurring repeated measures ANOVA design. Sixteen dogs are randomly assigned to four groups. (One animal is removed from the analysis due to a missing value for one dependent variable.) Dogs in each group receive either morphine or trimethaphan (variable Drug) and have either depleted or intact histamine levels (variable Depleted) before receiving the drugs. The dependent variable is the blood concentration of histamine at 0, 1, 3, and 5 minutes after injection of the drug. Logarithms are applied to these concentrations to minimize correlation between the mean and the variance of the data.
The following SAS statements perform both univariate and multivariate repeated measures analyses and produce Output 41.7.1 through Output 41.7.7.
data dogs;
input Drug $12. Depleted $ Histamine0 Histamine1
Histamine3 Histamine5;
LogHistamine0=log(Histamine0);
LogHistamine1=log(Histamine1);
LogHistamine3=log(Histamine3);
LogHistamine5=log(Histamine5);
datalines;
Morphine N .04 .20 .10 .08
Morphine N .02 .06 .02 .02
Morphine N .07 1.40 .48 .24
Morphine N .17 .57 .35 .24
Morphine Y .10 .09 .13 .14
Morphine Y .12 .11 .10 .
Morphine Y .07 .07 .06 .07
Morphine Y .05 .07 .06 .07
Trimethaphan N .03 .62 .31 .22
Trimethaphan N .03 1.05 .73 .60
Trimethaphan N .07 .83 1.07 .80
Trimethaphan N .09 3.13 2.06 1.23
Trimethaphan Y .10 .09 .09 .08
Trimethaphan Y .08 .09 .09 .10
Trimethaphan Y .13 .10 .12 .12
Trimethaphan Y .06 .05 .05 .05
;
proc glm;
class Drug Depleted;
model LogHistamine0--LogHistamine5 =
Drug Depleted Drug*Depleted / nouni;
repeated Time 4 (0 1 3 5) polynomial / summary printe;
run;
The NOUNI option in the MODEL statement suppresses the individual ANOVA tables for the original dependent variables. These analyses are usually of no interest in a repeated measures analysis. The POLYNOMIAL option in the REPEATED statement indicates that the transformation used to implement the repeated measures analysis is an orthogonal polynomial transformation, and the SUMMARY option requests that the univariate analyses for the orthogonal polynomial contrast variables be displayed. The parenthetical numbers (0 1 3 5) determine the spacing of the orthogonal polynomials used in the analysis.
| Class Level Information | ||
|---|---|---|
| Class | Levels | Values |
| Drug | 2 | Morphine Trimethaphan |
| Depleted | 2 | N Y |
| Number of Observations Read | 16 |
|---|---|
| Number of Observations Used | 15 |
The "Repeated Measures Level Information" table gives information about the repeated measures effect; it is displayed in Output 41.7.2. In this example, the within-subject (within-dog) effect is Time, which has the levels 0, 1, 3, and 5.
| Repeated Measures Level Information | ||||
|---|---|---|---|---|
| Dependent Variable | LogHistamine0 | LogHistamine1 | LogHistamine3 | LogHistamine5 |
| Level of Time | 0 | 1 | 3 | 5 |
The multivariate analyses for within-subject effects and related interactions are displayed in Output 41.7.3. For the example, the first table displayed shows that the TIME effect is significant. In addition, the Time*Drug*Depleted interaction is significant, as shown in the fourth table. This means that the effect of Time on the blood concentration of histamine is different for the four Drug*Depleted combinations studied.
| MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no Time Effect H = Type III SSCP Matrix for Time E = Error SSCP Matrix S=1 M=0.5 N=3.5 |
|||||
|---|---|---|---|---|---|
| Statistic | Value | F Value | Num DF | Den DF | Pr > F |
| Wilks' Lambda | 0.11097706 | 24.03 | 3 | 9 | 0.0001 |
| Pillai's Trace | 0.88902294 | 24.03 | 3 | 9 | 0.0001 |
| Hotelling-Lawley Trace | 8.01087137 | 24.03 | 3 | 9 | 0.0001 |
| Roy's Greatest Root | 8.01087137 | 24.03 | 3 | 9 | 0.0001 |
| MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no Time*Drug Effect H = Type III SSCP Matrix for Time*Drug E = Error SSCP Matrix S=1 M=0.5 N=3.5 |
|||||
|---|---|---|---|---|---|
| Statistic | Value | F Value | Num DF | Den DF | Pr > F |
| Wilks' Lambda | 0.34155984 | 5.78 | 3 | 9 | 0.0175 |
| Pillai's Trace | 0.65844016 | 5.78 | 3 | 9 | 0.0175 |
| Hotelling-Lawley Trace | 1.92774470 | 5.78 | 3 | 9 | 0.0175 |
| Roy's Greatest Root | 1.92774470 | 5.78 | 3 | 9 | 0.0175 |
| MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no Time*Depleted Effect H = Type III SSCP Matrix for Time*Depleted E = Error SSCP Matrix S=1 M=0.5 N=3.5 |
|||||
|---|---|---|---|---|---|
| Statistic | Value | F Value | Num DF | Den DF | Pr > F |
| Wilks' Lambda | 0.12339988 | 21.31 | 3 | 9 | 0.0002 |
| Pillai's Trace | 0.87660012 | 21.31 | 3 | 9 | 0.0002 |
| Hotelling-Lawley Trace | 7.10373567 | 21.31 | 3 | 9 | 0.0002 |
| Roy's Greatest Root | 7.10373567 | 21.31 | 3 | 9 | 0.0002 |
| MANOVA Test Criteria and Exact F Statistics for the Hypothesis of no Time*Drug*Depleted Effect H = Type III SSCP Matrix for Time*Drug*Depleted E = Error SSCP Matrix S=1 M=0.5 N=3.5 |
|||||
|---|---|---|---|---|---|
| Statistic | Value | F Value | Num DF | Den DF | Pr > F |
| Wilks' Lambda | 0.19383010 | 12.48 | 3 | 9 | 0.0015 |
| Pillai's Trace | 0.80616990 | 12.48 | 3 | 9 | 0.0015 |
| Hotelling-Lawley Trace | 4.15915732 | 12.48 | 3 | 9 | 0.0015 |
| Roy's Greatest Root | 4.15915732 | 12.48 | 3 | 9 | 0.0015 |
Output 41.7.4 displays tests of hypotheses for between-subject (between-dog) effects. This section tests the hypotheses that the different Drugs, Depleteds, and their interactions have no effects on the dependent variables, while ignoring the within-dog effects. From this analysis, there is a significant between-dog effect for Depleted (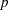 -value=0.0229). The interaction and the main effect for Drug are not significant (
-value=0.0229). The interaction and the main effect for Drug are not significant (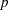 -values=0.1734 and 0.1281, respectively).
-values=0.1734 and 0.1281, respectively).
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Drug | 1 | 5.99336243 | 5.99336243 | 2.71 | 0.1281 |
| Depleted | 1 | 15.44840703 | 15.44840703 | 6.98 | 0.0229 |
| Drug*Depleted | 1 | 4.69087508 | 4.69087508 | 2.12 | 0.1734 |
| Error | 11 | 24.34683348 | 2.21334850 |
Univariate analyses for within-subject (within-dog) effects and related interactions are displayed in Output 41.7.6. The results for this example are the same as for the multivariate analyses; this is not always the case. In addition, before the univariate analyses are used to make conclusions about the data, the result of the sphericity test (requested with the PRINTE option in the REPEATED statement and displayed in Output 41.7.5) should be examined. If the sphericity test is rejected, consider using the adjusted G-G or H-F-L probabilities. See the section Repeated Measures Analysis of Variance for more information.
| Sphericity Tests | ||||
|---|---|---|---|---|
| Variables | DF | Mauchly's Criterion | Chi-Square | Pr > ChiSq |
| Transformed Variates | 5 | 0.1752641 | 16.930873 | 0.0046 |
| Orthogonal Components | 5 | 0.1752641 | 16.930873 | 0.0046 |
| Source | DF | Type III SS | Mean Square | F Value | Pr > F | Adj Pr > F | |
|---|---|---|---|---|---|---|---|
| G - G | H-F-L | ||||||
| Time | 3 | 12.05898677 | 4.01966226 | 53.44 | <.0001 | <.0001 | <.0001 |
| Time*Drug | 3 | 1.84429514 | 0.61476505 | 8.17 | 0.0003 | 0.0039 | 0.0023 |
| Time*Depleted | 3 | 12.08978557 | 4.02992852 | 53.57 | <.0001 | <.0001 | <.0001 |
| Time*Drug*Depleted | 3 | 2.93077939 | 0.97692646 | 12.99 | <.0001 | 0.0005 | 0.0002 |
| Error(Time) | 33 | 2.48238887 | 0.07522391 | ||||
| Greenhouse-Geisser Epsilon | 0.5694 |
|---|---|
| Huynh-Feldt-Lecoutre Epsilon | 0.6636 |
Output 41.7.7 is produced by the SUMMARY option in the REPEATED statement. If the POLYNOMIAL option is not used, a similar table is displayed using the default CONTRAST transformation. The linear, quadratic, and cubic trends for Time, labeled as ‘Time_1’, ‘Time_2’, and ‘Time_3’, are displayed, and in each case, the Source labeled ‘Mean’ gives a test for the respective trend.
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Mean | 1 | 2.00963483 | 2.00963483 | 34.99 | 0.0001 |
| Drug | 1 | 1.18069076 | 1.18069076 | 20.56 | 0.0009 |
| Depleted | 1 | 1.36172504 | 1.36172504 | 23.71 | 0.0005 |
| Drug*Depleted | 1 | 2.04346848 | 2.04346848 | 35.58 | <.0001 |
| Error | 11 | 0.63171161 | 0.05742833 |
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Mean | 1 | 5.40988418 | 5.40988418 | 57.15 | <.0001 |
| Drug | 1 | 0.59173192 | 0.59173192 | 6.25 | 0.0295 |
| Depleted | 1 | 5.94945506 | 5.94945506 | 62.86 | <.0001 |
| Drug*Depleted | 1 | 0.67031587 | 0.67031587 | 7.08 | 0.0221 |
| Error | 11 | 1.04118707 | 0.09465337 |
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Mean | 1 | 4.63946776 | 4.63946776 | 63.04 | <.0001 |
| Drug | 1 | 0.07187246 | 0.07187246 | 0.98 | 0.3443 |
| Depleted | 1 | 4.77860547 | 4.77860547 | 64.94 | <.0001 |
| Drug*Depleted | 1 | 0.21699504 | 0.21699504 | 2.95 | 0.1139 |
| Error | 11 | 0.80949018 | 0.07359002 |