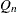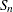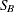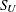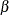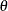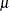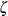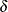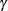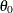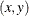The UNIVARIATE Procedure

INSET Statement

Subsections:

Statistical Keywords
Primary and Secondary Keywords
INSET Statistic Labels and Formats
Summary of Options
Dictionary of Options

INSET keywords </ options>;

An INSET statement places a box or table of summary statistics, called an inset, directly in a graph created with a CDFPLOT , HISTOGRAM , PPPLOT , PROBPLOT , or QQPLOT statement. The INSET statement must follow the plot statement that creates the plot that you want to augment. The inset appears in all the graphs that the preceding plot statement produces.

You can use multiple INSET statements after a plot statement to add more than one inset to a plot. See Example 4.17.

In an INSET statement, you specify one or more keywords that identify the information to display in the inset. The information is displayed in the order that you request the keywords. Keywords can be any of the following:

statistical keywords
primary keywords
secondary keywords

Statistical Keywords

The available statistical keywords are listed in Table 4.10.

Table 4.10: Statistical Keywords

Keyword	Description
Descriptive Statistic Keywords
CSS	Corrected sum of squares
CV	Coefficient of variation
GEOMEAN	Geometric mean
KURTOSIS \| KURT	Kurtosis
MAX	Largest value
MEAN	Sample mean
MIN	Smallest value
MODE	Most frequent value
N	Sample size
NEXCL	Number of observations excluded by MAXNBIN= or MAXSIGMAS= option
NMISS	Number of missing values
NOBS	Number of observations
RANGE	Range
SKEWNESS \| SKEW	Skewness
STD \| STDDEV	Standard deviation
STDMEAN \| STDERR	Standard error of the mean
SUM	Sum of the observations
SUMWGT	Sum of the weights
USS	Uncorrected sum of squares
VAR	Variance
Percentile Statistic Keywords
P1	1st percentile
P5	5th percentile
P10	10th percentile
Q1
P25	Lower quartile (25th percentile)
MEDIAN
Q2
P50	Median (50th percentile)
Q3
P75	Upper quartile (75th percentile)
P90	90th percentile
P95	95th percentile
P99	99th percentile
QRANGE	Interquartile range (Q3–Q1)
Keywords for Distribution-Free Confidence Limits for Percentiles (CIPCTLDF Option)
P1_LCL_DF	1st percentile lower confidence limit
P1_UCL_DF	1st percentile upper confidence limit
P5_LCL_DF	5th percentile lower confidence limit
P5_UCL_DF	5th percentile upper confidence limit
P10_LCL_DF	10th percentile lower confidence limit
P10_UCL_DF	10th percentile upper confidence limit
Q1_LCL_DF
P25_LCL_DF	Lower quartile (25th percentile) lower confidence limit
Q1_UCL_DF
P25_UCL_DF	Lower quartile (25th percentile) upper confidence limit
MEDIAN_LCL_DF
Q2_LCL_DF
P50_LCL_DF	Median (50th percentile) lower confidence limit
MEDIAN_UCL_DF
Q2_UCL_DF
P50_UCL_DF	Median (50th percentile) upper confidence limit
Q3_LCL_DF
P75_LCL_DF	Upper quartile (75th percentile) lower confidence limit
Q3_UCL_DF
P75_UCL_DF	Upper quartile (75th percentile) upper confidence limit
P90_LCL_DF	90th percentile lower confidence limit
P90_UCL_DF	90th percentile upper confidence limit
P95_LCL_DF	95th percentile lower confidence limit
P95_UCL_DF	95th percentile upper confidence limit
P99_LCL_DF	99th percentile lower confidence limit
P99_UCL_DF	99th percentile upper confidence limit
Keywords Percentile Confidence Limits Assuming Normality (CIPCTLNORMAL Option)
P1_LCL	1st percentile lower confidence limit
P1_UCL	1st percentile upper confidence limit
P5_LCL	5th percentile lower confidence limit
P5_UCL	5th percentile upper confidence limit
P10_LCL	10th percentile lower confidence limit
P10_UCL	10th percentile upper confidence limit
Q1_LCL
P25_LCL	Lower quartile (25th percentile) lower confidence limit
Q1_UCL
P25_UCL	Lower quartile (25th percentile) upper confidence limit
MEDIAN_LCL
Q2_LCL
P50_LCL	Median (50th percentile) lower confidence limit
MEDIAN_UCL
Q2_UCL
P50_UCL	Median (50th percentile) upper confidence limit
Q3_LCL
P75_LCL	Upper quartile (75th percentile) lower confidence limit
Q3_UCL
P75_UCL	Upper quartile (75th percentile) upper confidence limit
P90_LCL	90th percentile lower confidence limit
P90_UCL	90th percentile upper confidence limit
P95_LCL	95th percentile lower confidence limit
P95_UCL	95th percentile upper confidence limit
P99_LCL	99th percentile lower confidence limit
P99_UCL	99th percentile upper confidence limit
Robust Statistics Keywords
GINI	Gini’s mean difference
MAD	Median absolute difference about the median
QN	$Q_ n$ , alternative to MAD
SN	$S_ n$ , alternative to MAD
STD_GINI	Gini’s standard deviation
STD_MAD	MAD standard deviation
STD_QN	$Q_ n$ standard deviation
STD_QRANGE	Interquartile range standard deviation
STD_SN	$S_ n$ standard deviation
Hypothesis Testing Keywords
MSIGN	Sign statistic
NORMALTEST	Test statistic for normality
PNORMAL	Probability value for the test of normality
SIGNRANK	Signed rank statistic
PROBM	Probability of greater absolute value for the sign statistic
PROBN	Probability value for the test of normality
PROBS	Probability value for the signed rank test
PROBT	Probability value for the Student’s t test
T	Statistics for Student’s t test
Keyword for Reading an Input Data Set
DATA=	(label, value) pairs from input data set

To create a completely customized inset, use a DATA= data set.

DATA=SAS-data-set

requests that PROC UNIVARIATE display customized statistics from a SAS data set in the inset table. The data set must contain two variables:

_LABEL_: is a character variable whose values provide labels for inset entries.
_VALUE_: is a variable that is either character or numeric and whose values provide values for inset entries.

The label and value from each observation in the data set occupy one line in the inset. The position of the DATA= keyword in the keyword list determines the position of its lines in the inset.

Primary and Secondary Keywords

A primary keyword specifies a fitted distribution, which is one of the parametric distributions or a kernel density estimate. You specify secondary keywords in parentheses after the primary keyword to request particular statistics associated with that distribution.

Note: When producing traditional graphics output, you can specify a primary keyword without secondary keywords to display a colored line and the distribution name as a key for the density curve.

In the HISTOGRAM statement you can request more than one fitted distribution from the same family (for example, two normal distributions). You can display inset statistics for individual curves by specifying the curve indices in square brackets immediately following the primary keyword.

The following statements produce a histogram with three fitted normal curves and an inset that contains goodness-of-fit statistics for the second curve only:

proc univariate data=score;
   histogram final / normal(sigma=1 2 3);
   inset normal[2](ad adpval);
run;

Table 4.11 lists the primary keywords and the plot statements with which they can be specified.

Table 4.11: Primary Keywords

Keyword	Distribution	Plot Statement Availability
BETA	Beta	All plot statements
EXPONENTIAL	Exponential	All plot statements
GAMMA	Gamma	All plot statements
GUMBEL	Gumbel	All plot statements
IGAUSS	Inverse Gaussian	CDFPLOT, HISTOGRAM, PPPLOT
KERNEL	Kernel density estimate	HISTOGRAM
LOGNORMAL	Lognormal	All plot statements
NORMAL	Normal	All plot statements
PARETO	Pareto	All plot statements
POWER	Power function	All plot statements
RAYLEIGH	Rayleigh	All plot statements
SB	Johnson $S_ B$	HISTOGRAM
SU	Johnson $S_ U$	HISTOGRAM
WEIBULL	Weibull(3-parameter)	All plot statements
WEIBULL2	Weibull(2-parameter)	PROBPLOT, QQPLOT

Table 4.12 lists the secondary keywords available with the primary keywords listed in Table 4.11.

Table 4.12: Secondary Keywords

Secondary Keyword	Alias	Description
BETA Secondary Keywords
ALPHA	SHAPE1	First shape parameter $\alpha$
BETA	SHAPE2	Second shape parameter $\beta$
MEAN		Mean of the fitted distribution
SIGMA	SCALE	Scale parameter $\sigma$
STD		Standard deviation of the fitted distribution
THETA	THRESHOLD	Lower threshold parameter $\theta$
EXPONENTIAL Secondary Keywords
MEAN		Mean of the fitted distribution
SIGMA	SCALE	Scale parameter $\sigma$
STD		Standard deviation of the fitted distribution
THETA	THRESHOLD	Threshold parameter $\theta$
GAMMA Secondary Keywords
ALPHA	SHAPE	Shape parameter $\alpha$
MEAN		Mean of the fitted distribution
SIGMA	SCALE	Scale parameter $\sigma$
STD		Standard deviation of the fitted distribution
THETA	THRESHOLD	Threshold parameter $\theta$
GUMBEL Secondary Keywords
MEAN		Mean of the fitted distribution
MU		Location parameter $\mu$
SIGMA	SCALE	Scale parameter $\sigma$
STD		Standard deviation of the fitted distribution
IGAUSS Secondary Keywords
LAMBDA		Shape parameter $\lambda$
MEAN		Mean of the fitted distribution
MU		Mean parameter $\mu$
STD		Standard deviation of the fitted distribution
KERNEL Secondary Keywords
AMISE		Approximate mean integrated square error (MISE) for the kernel density
BANDWIDTH		Bandwidth $\lambda$ for the density estimate
BWIDTH		Alias for BANDWIDTH
C		Standardized bandwidth for the density estimate
TYPE		Kernel type: normal, quadratic, or triangular
LOGNORMAL Secondary Keywords
MEAN		Mean of the fitted distribution
SIGMA	SHAPE	Shape parameter $\sigma$
STD		Standard deviation of the fitted distribution
THETA	THRESHOLD	Threshold parameter $\theta$
ZETA	SCALE	Scale parameter $\zeta$
NORMAL Secondary Keywords
MU	MEAN	Mean parameter $\mu$
SIGMA	STD	Scale parameter $\sigma$
PARETO Secondary Keywords
ALPHA		Shape parameter $\alpha$
MEAN		Mean of the fitted distribution
SIGMA	SCALE	Scale parameter $\sigma$
STD		Standard deviation of the fitted distribution
THETA	THRESHOLD	Threshold parameter $\theta$
POWER Secondary Keywords
ALPHA		Shape parameter $\alpha$
MEAN		Mean of the fitted distribution
SIGMA	SCALE	Scale parameter $\sigma$
STD		Standard deviation of the fitted distribution
THETA	THRESHOLD	Threshold parameter $\theta$
RAYLEIGH Secondary Keywords
MEAN		Mean of the fitted distribution
SIGMA	SCALE	Scale parameter $\sigma$
STD		Standard deviation of the fitted distribution
THETA	THRESHOLD	Threshold parameter $\theta$
SB and SU Secondary Keywords
DELTA	SHAPE1	First shape parameter $\delta$
GAMMA	SHAPE2	Second shape parameter $\gamma$
MEAN		Mean of the fitted distribution
SIGMA	SCALE	Scale parameter $\sigma$
STD		Standard deviation of the fitted distribution
THETA	THRESHOLD	Lower threshold parameter $\theta$
WEIBULL Secondary Keywords
C	SHAPE	Shape parameter c
MEAN		Mean of the fitted distribution
SIGMA	SCALE	Scale parameter $\sigma$
STD		Standard deviation of the fitted distribution
THETA	THRESHOLD	Threshold parameter $\theta$
WEIBULL2 Secondary Keywords
C	SHAPE	Shape parameter c
MEAN		Mean of the fitted distribution
SIGMA	SCALE	Scale parameter $\sigma$
STD		Standard deviation of the fitted distribution
THETA	THRESHOLD	Known lower threshold $\theta _0$
Keywords Available for All Parametric (non-KERNEL) Distributions
AD		Anderson-Darling EDF test statistic
ADPVAL		Anderson-Darling EDF test p-value
CVM		Cramér–von Mises EDF test statistic
CVMPVAL		Cramér–von Mises EDF test p-value
KSD		Kolmogorov-Smirnov EDF test statistic
KSDPVAL		Kolmogorov-Smirnov EDF test p-value

The inset statistics listed in Table 4.12 are not available unless you request a plot statement and options that calculate these statistics. For example, consider the following statements:

proc univariate data=score;
   histogram final / normal;
   inset mean std normal(ad adpval);
run;

The MEAN and STD keywords display the sample mean and standard deviation, respectively, of final. The NORMAL keyword with the secondary keywords AD and ADPVAL displays the Anderson-Darling goodness-of-fit test statistic and p-value, respectively. The statistics that are specified with the NORMAL keyword are available only because the NORMAL option is requested in the HISTOGRAM statement.

The KERNEL keyword is available only if you request a kernel density estimate in a HISTOGRAM statement. The WEIBULL2 keyword is available only if you request a two-parameter Weibull distribution in the PROBPLOT or QQPLOT statement.

INSET Statistic Labels and Formats

By default, PROC UNIVARIATE identifies inset statistics with appropriate labels and prints numeric values with appropriate formats. To customize the label, specify the keyword followed by an equal sign (=) and the desired label in quotes. To customize the format, specify a numeric format in parentheses after the keyword. Labels can have up to 24 characters. If you specify both a label and a format for a statistic, the label must appear before the format. For example, the following statement requests customized labels for two statistics and displays the standard deviation with a field width of 5 and two decimal places:

inset n='Sample Size' std='Std Dev' (5.2);

Summary of Options

Table 4.13 lists INSET statement options, which are specified after the slash (/) in the INSET statement. For complete descriptions, see the section Dictionary of Options.

Table 4.13: INSET Options

Option	Description
CFILL=color \| BLANK	specifies color of inset background
CFILLH=color	specifies color of header background
CFRAME=color	specifies color of frame
CHEADER=color	specifies color of header text
CSHADOW=color	specifies color of drop shadow
CTEXT=color	specifies color of inset text
DATA	specifies data units for POSITION= $(x,y)$ coordinates
FONT=font	specifies font of text
FORMAT=format	specifies format of values in inset
GUTTER=value	specifies gutter width for inset in top or bottom margin
HEADER='string'	specifies header text
HEIGHT=value	specifies height of inset text
NCOLS=	specifies number of columns for inset in top or bottom margin
NOFRAME	suppresses frame around inset
POSITION=position	specifies position of inset
REFPOINT=BR \| BL \| TR \| TL	specifies reference point of inset positioned with POSITION= $(x,y)$ coordinates

Dictionary of Options

The following entries provide detailed descriptions of options for the INSET statement. Options marked with † are applicable only when traditional graphics are produced.

† CFILL=color | BLANK

specifies the color of the background for traditional graphics. If you omit the CFILLH= option the header background is included. By default, the background is empty, which causes items that overlap the inset (such as curves or histogram bars) to show through the inset.

If you specify a value for CFILL= option, then overlapping items no longer show through the inset. Use CFILL=BLANK to leave the background uncolored and to prevent items from showing through the inset.

† CFILLH=color

specifies the color of the header background for traditional graphics. The default value is the CFILL= color.

† CFRAME=color

specifies the color of the frame for traditional graphics. The default value is the same color as the axis of the plot.

† CHEADER=color

specifies the color of the header text for traditional graphics. The default value is the CTEXT= color.

† CSHADOW=color

specifies the color of the drop shadow for traditional graphics. By default, if a CSHADOW= option is not specified, a drop shadow is not displayed.

† CTEXT=color

specifies the color of the text for traditional graphics. The default value is the same color as the other text on the plot.

DATA

specifies that data coordinates are to be used in positioning the inset with the POSITION= option. The DATA option is available only when you specify POSITION=(x,y). You must place DATA immediately after the coordinates (x,y). Note: Positioning insets with coordinates is not supported for ODS Graphics output.

† FONT=font

specifies the font of the text for traditional graphics. By default, if you locate the inset in the interior of the plot, then the font is SIMPLEX. If you locate the inset in the exterior of the plot, then the font is the same as the other text on the plot.

FORMAT=format

specifies a format for all the values in the inset. If you specify a format for a particular statistic, then that format overrides the one specified with the FORMAT= option. For more information about SAS formats, see SAS Formats and Informats: Reference.

GUTTER=value

specifies the gutter width in percent screen units for an inset located in the top or bottom margin. The gutter is the space between columns of (label, value) pairs in an inset. The default value is four. Note: The GUTTER= option applies only when ODS Graphics is enabled.

HEADER=string

specifies the header text. The string cannot exceed 40 characters. By default, no header line appears in the inset. If all the keywords that you list in the INSET statement are secondary keywords that correspond to a fitted curve on a histogram, PROC UNIVARIATE displays a default header that indicates the distribution and identifies the curve.

† HEIGHT=value

specifies the height of the text for traditional graphics.

NCOLS=n

specifies the number of columns of (label, value) pairs displayed in an inset located in the top or bottom margin. The default value is three. Note: The NCOLS= option applies only when ODS Graphics is enabled.

NOFRAME

suppresses the frame drawn around the text.

POSITION=position POS=position

determines the position of the inset. The position is a compass point keyword, a margin keyword, or a pair of coordinates (x,y). You can specify coordinates in axis percent units or axis data units. The default value is NW, which positions the inset in the upper left (northwest) corner of the display. See the section Positioning Insets.

Note: Positioning insets with coordinates is not supported for ODS Graphics output.

† REFPOINT=BR | BL | TR | TL

specifies the reference point for an inset that PROC UNIVARIATE positions by a pair of coordinates with the POSITION= option. The REFPOINT= option specifies which corner of the inset frame that you want to position at coordinates (x,y). The keywords are BL, BR, TL, and TR, which correspond to bottom left, bottom right, top left, and top right. The default value is BL. You must use REFPOINT= with POSITION=(x,y) coordinates. The option does not apply to ODS Graphics output.