The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources
Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources -
Examples
 Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Basic Summary PlotsAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot
Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Basic Summary PlotsAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot - References
Example 4.34 Comparing Weibull Quantile Plots
This example compares the use of three-parameter and two-parameter Weibull Q-Q plots for the failure times in months for 48
integrated circuits. The times are assumed to follow a Weibull distribution. The following statements save the failure times
as the values of the variable Time in the data set Failures:
data Failures; input Time @@; label Time = 'Time in Months'; datalines; 29.42 32.14 30.58 27.50 26.08 29.06 25.10 31.34 29.14 33.96 30.64 27.32 29.86 26.28 29.68 33.76 29.32 30.82 27.26 27.92 30.92 24.64 32.90 35.46 30.28 28.36 25.86 31.36 25.26 36.32 28.58 28.88 26.72 27.42 29.02 27.54 31.60 33.46 26.78 27.82 29.18 27.94 27.66 26.42 31.00 26.64 31.44 32.52 ;
If no assumption is made about the parameters of this distribution, you can use the WEIBULL option to request a three-parameter Weibull plot. As in the previous example, you can visually estimate the shape parameter c by requesting plots for different values of c and choosing the value of c that linearizes the point pattern. Alternatively, you can request a maximum likelihood estimate for c, as illustrated in the following statements:
title 'Three-Parameter Weibull Q-Q Plot for Failure Times';
ods graphics on;
proc univariate data=Failures noprint;
qqplot Time / weibull(c=est theta=est sigma=est)
square
href = 0.5 1 1.5 2
vref = 25 27.5 30 32.5 35
odstitle = title;
run;
Note: When using the WEIBULL option, you must either specify a list of values for the Weibull shape parameter c with the C= option or specify C=EST.
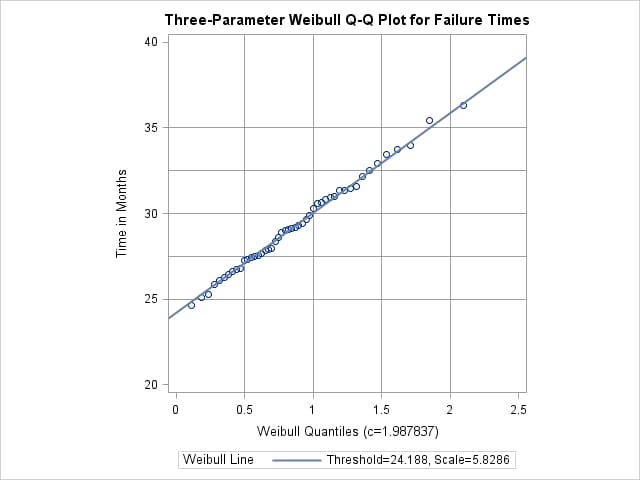
Output 4.34.1 displays the plot for the estimated value 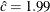 . The reference line corresponds to the estimated values for the threshold and scale parameters of
. The reference line corresponds to the estimated values for the threshold and scale parameters of 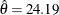 and
and 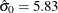 , respectively.
, respectively.
Output 4.34.1: Three-Parameter Weibull Q-Q Plot
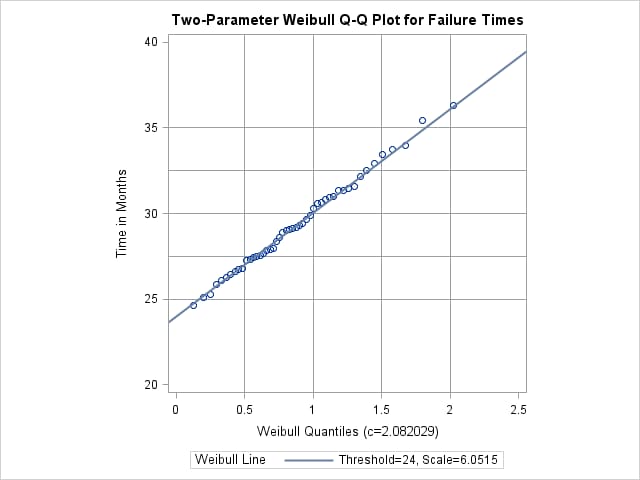
Now, suppose it is known that the circuit lifetime is at least 24 months. The following statements use the known threshold
value 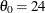 to produce the two-parameter Weibull Q-Q plot shown in Output 4.31.4:
to produce the two-parameter Weibull Q-Q plot shown in Output 4.31.4:
title 'Two-Parameter Weibull Q-Q Plot for Failure Times';
proc univariate data=Failures noprint;
qqplot Time / weibull(theta=24 c=est sigma=est)
square
vref = 25 to 35 by 2.5
href = 0.5 to 2.0 by 0.5
odstitle = title;
run;
The reference line is based on maximum likelihood estimates 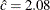 and
and 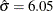 .
.
Output 4.34.2: Two-Parameter Weibull Q-Q Plot for 
A sample program for this example, uniex19.sas, is available in the SAS Sample Library for Base SAS software.