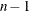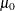The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources
Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources -
Examples
 Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Basic Summary PlotsAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot
Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Basic Summary PlotsAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot - References
OUT= Output Data Set in the OUTPUT Statement
PROC UNIVARIATE creates an OUT= data set for each OUTPUT statement. This data set contains an observation for each combination of levels of the variables in the BY statement, or a single observation if you do not specify a BY statement. Thus the number of observations in the new data set corresponds to the number of groups for which statistics are calculated. Without a BY statement, the procedure computes statistics and percentiles by using all the observations in the input data set. With a BY statement, the procedure computes statistics and percentiles by using the observations within each BY group.
The variables in the OUT= data set are as follows:
-
BY statement variables. The values of these variables match the values in the corresponding BY group in the DATA= data set and indicate which BY group each observation summarizes.
-
variables created by selecting statistics in the OUTPUT statement. The statistics are computed using all the nonmissing data, or they are computed for each BY group if you use a BY statement.
-
variables created by requesting new percentiles with the PCTLPTS= option. The names of these new variables depend on the values of the PCTLPRE= and PCTLNAME= options.
If the output data set contains a percentile variable or a quartile variable, the percentile definition assigned with the PCTLDEF= option in the PROC UNIVARIATE statement is recorded in the output data set label. See Example 4.8.
The following table lists variables available in the OUT= data set.
Table 4.36: Variables Available in the OUT= Data Set
|
Variable Name |
Description |
|---|---|
|
Descriptive Statistics |
|
|
CSS |
sum of squares corrected for the mean |
|
CV |
percent coefficient of variation |
|
KURTOSIS | KURT |
measurement of the heaviness of tails |
|
MAX |
largest (maximum) value |
|
MEAN |
arithmetic mean |
|
MIN |
smallest (minimum) value |
|
MODE |
most frequent value (if not unique, the smallest mode) |
|
N |
number of observations on which calculations are based |
|
NMISS |
number of missing observations |
|
NOBS |
total number of observations |
|
RANGE |
difference between the maximum and minimum values |
|
SKEWNESS | SKEW |
measurement of the tendency of the deviations to be larger in one direction than in the other |
|
STD | STDDEV |
standard deviation |
|
STDMEAN | STDERR |
standard error of the mean |
|
SUM |
sum |
|
SUMWGT |
sum of the weights |
|
USS |
uncorrected sum of squares |
|
VAR |
variance |
|
Quantile Statistics |
|
|
MEDIAN | Q2 | P50 |
middle value (50th percentile) |
|
P1 |
1st percentile |
|
P5 |
5th percentile |
|
P10 |
10th percentile |
|
P90 |
90th percentile |
|
P95 |
95th percentile |
|
P99 |
99th percentile |
|
Q1 | P25 |
lower quartile (25th percentile) |
|
Q3 | P75 |
upper quartile (75th percentile) |
|
QRANGE |
difference between the upper and lower quartiles (also known as the inner quartile range) |
|
Robust Statistics |
|
|
GINI |
Gini’s mean difference |
|
MAD |
median absolute difference |
|
QN |
2nd variation of median absolute difference |
|
SN |
1st variation of median absolute difference |
|
STD_GINI |
standard deviation for Gini’s mean difference |
|
STD_MAD |
standard deviation for median absolute difference |
|
STD_QN |
standard deviation for the second variation of the median absolute difference |
|
STD_QRANGE |
estimate of the standard deviation, based on interquartile range |
|
STD_SN |
standard deviation for the first variation of the median absolute difference |
|
Hypothesis Test Statistics |
|
|
MSIGN |
sign statistic |
|
NORMAL |
test statistic for normality. If the sample size is less than or equal to 2000, this is the Shapiro-Wilk W statistic. Otherwise, it is the Kolmogorov D statistic. |
|
PROBM |
probability of a greater absolute value for the sign statistic |
|
PROBN |
probability that the data came from a normal distribution |
|
PROBS |
probability of a greater absolute value for the signed rank statistic |
|
PROBT |
two-tailed p-value for Student’s t statistic with |
|
SIGNRANK |
signed rank statistic |
|
T |
Student’s t statistic to test the null hypothesis that the population mean is equal to |