The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources
Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources -
Examples
 Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Basic Summary PlotsAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot
Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Basic Summary PlotsAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot - References
Confidence Limits for Parameters of the Normal Distribution
The two-sided 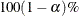 confidence interval for the mean has upper and lower limits
confidence interval for the mean has upper and lower limits
![\[ \bar{x} \pm t_{1-\frac{\alpha }{2};n-1}\frac{s}{\sqrt {n}} \]](images/procstat_univariate0222.png)
where 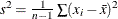 and
and 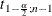 is the
is the 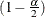 percentile of the t distribution with
percentile of the t distribution with 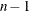 degrees of freedom. The one-sided upper
degrees of freedom. The one-sided upper 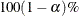 confidence limit is computed as
confidence limit is computed as 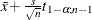 and the one-sided lower
and the one-sided lower 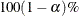 confidence limit is computed as
confidence limit is computed as 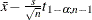 . See Example 4.9.
. See Example 4.9.
The two-sided 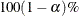 confidence interval for the standard deviation has lower and upper limits,
confidence interval for the standard deviation has lower and upper limits,
![\[ \begin{array}{ccc} s \sqrt {\frac{n-1}{\chi ^2_{1-\frac{\alpha }{2};n-1}}} & \mbox{and} & s \sqrt {\frac{n-1}{\chi ^2_{\frac{\alpha }{2};n-1}}} \end{array} \]](images/procstat_univariate0228.png)
respectively, where 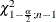 and
and 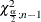 are the
are the 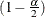 and
and 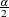 percentiles of the chi-square distribution with
percentiles of the chi-square distribution with 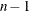 degrees of freedom. A one-sided
degrees of freedom. A one-sided 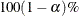 confidence limit has lower and upper limits,
confidence limit has lower and upper limits,
![\[ \begin{array}{ccc} s \sqrt {\frac{n-1}{\chi ^2_{1-\alpha ;n-1}}} & \mbox{and} & s \sqrt {\frac{n-1}{\chi ^2_{\alpha ;n-1}}} \end{array} \]](images/procstat_univariate0231.png)
respectively. The 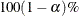 confidence interval for the variance has upper and lower limits equal to the squares of the corresponding upper and lower
limits for the standard deviation.
confidence interval for the variance has upper and lower limits equal to the squares of the corresponding upper and lower
limits for the standard deviation.
When you use the WEIGHT statement and specify VARDEF=DF in the PROC statement, the 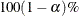 confidence interval for the weighted mean is
confidence interval for the weighted mean is
![\[ \bar{x}_ w \pm t_{1-\frac{\alpha }{2}} \frac{s_ w}{\sqrt {\sum _{i=1}^ n w_ i}} \]](images/procstat_univariate0232.png)
where 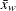 is the weighted mean,
is the weighted mean, 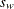 is the weighted standard deviation,
is the weighted standard deviation, 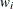 is the weight for ith observation, and
is the weight for ith observation, and 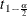 is the
is the 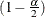 percentile for the t distribution with
percentile for the t distribution with 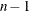 degrees of freedom.
degrees of freedom.
Confidence intervals for the weighted standard deviation are computed by substituting 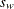 for s in the preceding formulas for confidence limits for the standard deviation.
for s in the preceding formulas for confidence limits for the standard deviation.