The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources
Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources -
Examples
 Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Plots for Line Printer OutputAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot
Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Plots for Line Printer OutputAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot - References
To determine an appropriate model for a data distribution, you should consider curves from several distribution families. As shown in this example, you can use the HISTOGRAM statement to fit more than one distribution and display the density curves on a histogram.
The gap between two plates is measured (in cm) for each of 50 welded assemblies selected at random from the output of a welding
process. The following statements save the measurements (Gap) in a data set named Plates:
data Plates; label Gap = 'Plate Gap in cm'; input Gap @@; datalines; 0.746 0.357 0.376 0.327 0.485 1.741 0.241 0.777 0.768 0.409 0.252 0.512 0.534 1.656 0.742 0.378 0.714 1.121 0.597 0.231 0.541 0.805 0.682 0.418 0.506 0.501 0.247 0.922 0.880 0.344 0.519 1.302 0.275 0.601 0.388 0.450 0.845 0.319 0.486 0.529 1.547 0.690 0.676 0.314 0.736 0.643 0.483 0.352 0.636 1.080 ;
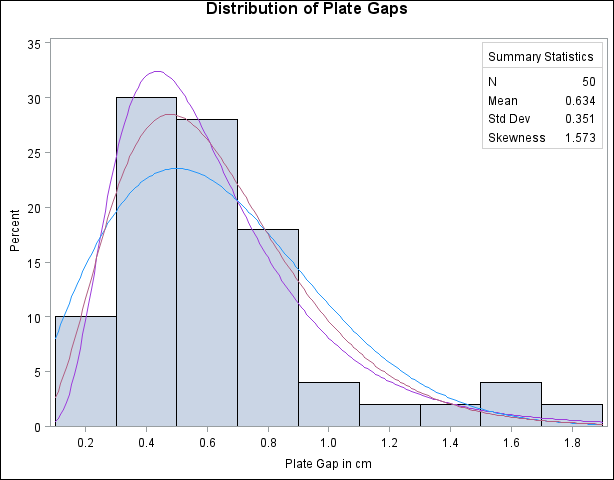
The following statements fit three distributions (lognormal, Weibull, and gamma) and display their density curves on a single histogram:
title 'Distribution of Plate Gaps';
ods graphics off;
ods select ParameterEstimates GoodnessOfFit FitQuantiles MyHist;
proc univariate data=Plates;
var Gap;
histogram / midpoints=0.2 to 1.8 by 0.2
lognormal
weibull
gamma
vaxis = axis1
name = 'MyHist';
inset n mean(5.3) std='Std Dev'(5.3) skewness(5.3)
/ pos = ne header = 'Summary Statistics';
axis1 label=(a=90 r=0);
run;
The ODS SELECT statement restricts the output to the “ParameterEstimates,” “GoodnessOfFit,” and “FitQuantiles” tables; see the section ODS Table Names. The LOGNORMAL, WEIBULL, and GAMMA primary options request superimposed fitted curves on the histogram in Output 4.22.1. Note that a threshold parameter ![]() is assumed for each curve. In applications where the threshold is not zero, you can specify
is assumed for each curve. In applications where the threshold is not zero, you can specify ![]() with the THETA= secondary option.
with the THETA= secondary option.
The LOGNORMAL, WEIBULL, and GAMMA options also produce the summaries for the fitted distributions shown in Output 4.22.2 through Output 4.22.4.
Output 4.22.2 provides three EDF goodness-of-fit tests for the lognormal distribution: the Anderson-Darling, the Cramér-von Mises, and
the Kolmogorov-Smirnov tests. At the ![]() significance level, all tests support the conclusion that the two-parameter lognormal distribution with scale parameter
significance level, all tests support the conclusion that the two-parameter lognormal distribution with scale parameter ![]() and shape parameter
and shape parameter ![]() provides a good model for the distribution of plate gaps.
provides a good model for the distribution of plate gaps.
Output 4.22.2: Summary of Fitted Lognormal Distribution
| Distribution of Plate Gaps |
| Parameters for Lognormal Distribution | ||
|---|---|---|
| Parameter | Symbol | Estimate |
| Threshold | Theta | 0 |
| Scale | Zeta | -0.58375 |
| Shape | Sigma | 0.499546 |
| Mean | 0.631932 | |
| Std Dev | 0.336436 | |
| Goodness-of-Fit Tests for Lognormal Distribution | ||||
|---|---|---|---|---|
| Test | Statistic | p Value | ||
| Kolmogorov-Smirnov | D | 0.06441431 | Pr > D | >0.150 |
| Cramer-von Mises | W-Sq | 0.02823022 | Pr > W-Sq | >0.500 |
| Anderson-Darling | A-Sq | 0.24308402 | Pr > A-Sq | >0.500 |
| Quantiles for Lognormal Distribution | ||
|---|---|---|
| Percent | Quantile | |
| Observed | Estimated | |
| 1.0 | 0.23100 | 0.17449 |
| 5.0 | 0.24700 | 0.24526 |
| 10.0 | 0.29450 | 0.29407 |
| 25.0 | 0.37800 | 0.39825 |
| 50.0 | 0.53150 | 0.55780 |
| 75.0 | 0.74600 | 0.78129 |
| 90.0 | 1.10050 | 1.05807 |
| 95.0 | 1.54700 | 1.26862 |
| 99.0 | 1.74100 | 1.78313 |
Output 4.22.3: Summary of Fitted Weibull Distribution
| Distribution of Plate Gaps |
| Parameters for Weibull Distribution | ||
|---|---|---|
| Parameter | Symbol | Estimate |
| Threshold | Theta | 0 |
| Scale | Sigma | 0.719208 |
| Shape | C | 1.961159 |
| Mean | 0.637641 | |
| Std Dev | 0.339248 | |
| Goodness-of-Fit Tests for Weibull Distribution | ||||
|---|---|---|---|---|
| Test | Statistic | p Value | ||
| Cramer-von Mises | W-Sq | 0.15937281 | Pr > W-Sq | 0.016 |
| Anderson-Darling | A-Sq | 1.15693542 | Pr > A-Sq | <0.010 |
| Quantiles for Weibull Distribution | ||
|---|---|---|
| Percent | Quantile | |
| Observed | Estimated | |
| 1.0 | 0.23100 | 0.06889 |
| 5.0 | 0.24700 | 0.15817 |
| 10.0 | 0.29450 | 0.22831 |
| 25.0 | 0.37800 | 0.38102 |
| 50.0 | 0.53150 | 0.59661 |
| 75.0 | 0.74600 | 0.84955 |
| 90.0 | 1.10050 | 1.10040 |
| 95.0 | 1.54700 | 1.25842 |
| 99.0 | 1.74100 | 1.56691 |
Output 4.22.3 provides two EDF goodness-of-fit tests for the Weibull distribution: the Anderson-Darling and the Cramér–von Mises tests.
The ![]() -values for the EDF tests are all less than 0.10, indicating that the data do not support a Weibull model.
-values for the EDF tests are all less than 0.10, indicating that the data do not support a Weibull model.
Output 4.22.4: Summary of Fitted Gamma Distribution
| Distribution of Plate Gaps |
| Parameters for Gamma Distribution | ||
|---|---|---|
| Parameter | Symbol | Estimate |
| Threshold | Theta | 0 |
| Scale | Sigma | 0.155198 |
| Shape | Alpha | 4.082646 |
| Mean | 0.63362 | |
| Std Dev | 0.313587 | |
| Goodness-of-Fit Tests for Gamma Distribution | ||||
|---|---|---|---|---|
| Test | Statistic | p Value | ||
| Kolmogorov-Smirnov | D | 0.09695325 | Pr > D | >0.250 |
| Cramer-von Mises | W-Sq | 0.07398467 | Pr > W-Sq | >0.250 |
| Anderson-Darling | A-Sq | 0.58106613 | Pr > A-Sq | 0.137 |
| Quantiles for Gamma Distribution | ||
|---|---|---|
| Percent | Quantile | |
| Observed | Estimated | |
| 1.0 | 0.23100 | 0.13326 |
| 5.0 | 0.24700 | 0.21951 |
| 10.0 | 0.29450 | 0.27938 |
| 25.0 | 0.37800 | 0.40404 |
| 50.0 | 0.53150 | 0.58271 |
| 75.0 | 0.74600 | 0.80804 |
| 90.0 | 1.10050 | 1.05392 |
| 95.0 | 1.54700 | 1.22160 |
| 99.0 | 1.74100 | 1.57939 |
Output 4.22.4 provides three EDF goodness-of-fit tests for the gamma distribution: the Anderson-Darling, the Cramér–von Mises, and the
Kolmogorov-Smirnov tests. At the ![]() significance level, all tests support the conclusion that the gamma distribution with scale parameter
significance level, all tests support the conclusion that the gamma distribution with scale parameter ![]() and shape parameter
and shape parameter ![]() provides a good model for the distribution of plate gaps.
provides a good model for the distribution of plate gaps.
Based on this analysis, the fitted lognormal distribution and the fitted gamma distribution are both good models for the distribution of plate gaps.
A sample program for this example, uniex13.sas, is available in the SAS Sample Library for Base SAS software.