The OPTNET Procedure

TSP Statement

TSP < options > ;

The TSP statement invokes an algorithm that solves the traveling salesman problem.

The traveling salesman problem is described in the section Traveling Salesman Problem. The algorithm that is used to solve this problem is built around the same method as is used in PROC OPTMILP: a branch-and-cut algorithm. Many of the options below are the same as those described for PROC OPTMILP in the SAS/OR User's Guide: Mathematical Programming.

You can specify the following options:

ABSOBJGAP=number

specifies a stopping criterion. When the absolute difference between the best integer objective and the objective of the best remaining branch-and-bound node becomes less than the value of number, the procedure stops. The value of number can be any nonnegative number; the default value is 1E–6.

CUTOFF=number

cuts off any branch-and-bound nodes in a minimization problem with an objective value that is greater than number. The value of number can be any number; the default value is the positive number that has the largest absolute value that can be represented in your operating environment.

CUTSTRATEGY=option

specifies the level of cuts to be generated by PROC OPTNET. Table 2.23 lists the valid values for this option.

Table 2.23: Values for CUTSTRATEGY= Option

number	string	Description
–1	AUTOMATIC	Disables most of the generic mixed-integer programming cuts and focuses on the generation of TSP-specific cuts
0	NONE	Disables generation of cutting planes
1	MODERATE	Uses a moderate cut strategy
2	AGGRESSIVE	Uses an aggressive cut strategy

The default is AUTOMATIC.

EMPHASIS=number | string

specifies a search emphasis option or its corresponding value number as listed in Table 2.24.

Table 2.24: Values for EMPHASIS= Option

number	string	Description
0	BALANCE	Performs a balanced search
1	OPTIMAL	Emphasizes optimality over feasibility
2	FEASIBLE	Emphasizes feasibility over optimality

The default is BALANCE.

HEURISTICS=number | string

controls the level of initial and primal heuristics that are applied by PROC OPTNET. This level determines how frequently primal heuristics are applied during the branch-and-bound tree search. It also affects the maximum number of iterations that are allowed in iterative heuristics. Some computationally expensive heuristics might be disabled by the solver at less aggressive levels. Table 2.25 lists the valid values for this option.

Table 2.25: Values for HEURISTICS= Option

number	string	Description
–1	AUTOMATIC	Applies the default level of heuristics
0	NONE	Disables all initial and primal heuristics
1	BASIC	Applies basic intial and primal heuristics at low frequency
2	MODERATE	Applies most intial and primal heuristics at moderate frequency
3	AGGRESSIVE	Applies all intitial primal heuristics at high frequency

The default is AUTOMATIC.

INTTOL=number

specifies the amount by which an integer variable value can differ from an integer and still be considered integer feasible. The value of number can be any number between 0.0 and 1.0; the default value is 1E–5. PROC OPTNET attempts to find an optimal solution with integer infeasibility less than number. If you assign a value that is less than 1E–10 to number and the best solution found by PROC OPTNET has integer infeasibility between number and 1E–10, then PROC OPTNET ends with a solution status of OPTIMAL_COND (see the section TSP).

LOGFREQ=number

specifies how often to print information in the branch-and-bound node log. The value of number can be any nonnegative integer up to the largest four-byte signed integer, which is 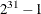$2^{31} - 1$ . The default value is 100. If number is set to 0, then the node log is disabled. If number is positive, then an entry is made in the node log at the first node, at the last node, and at intervals that are dictated by the value of number. An entry is also made each time a better integer solution is found.

LOGLEVEL=number | string

controls the amount of information displayed in the SAS log by the solver, from a short description of presolve information and summary to details at each branch-and-bound node. Table 2.26 describes the valid values for this option.

Table 2.26: Values for LOGLEVEL= Option

number	string	Description
0	NONE	Turns off all solver-related messages in the SAS log
1	BASIC	Displays a solver summary after stopping
2	MODERATE	Prints a solver summary and a node log by using the interval dictated by the LOGFREQ= option
3	AGGRESSIVE	Prints a detailed solver summary and a node log by using the interval dictated by the LOGFREQ= option

The default value is MODERATE.

MAXNODES=number

specifies the maximum number of branch-and-bound nodes to be processed. The value of number can be any nonnegative integer up to the largest four-byte signed integer, which is 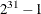$2^{31} - 1$ . The default value is $2^{31} - 1$ .

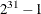MAXSOLS=number

specifies a stopping criterion. If number solutions have been found, then the procedure stops. The value of number can be any positive integer up to the largest four-byte signed integer, which is 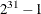$2^{31} - 1$ . The default value is $2^{31} - 1$ .

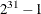MAXTIME=number

specifies the maximum amount of time to spend solving the traveling salesman problem. The type of time (either CPU time or real time) is determined by the value of the TIMETYPE= option. The value of number can be any positive number; the default value is the positive number that has the largest absolute value that can be represented in your operating environment.

MILP=number | string

specifies whether to use a mixed-integer linear programming (MILP) solver for solving the traveling salesman problem. The MILP solver attempts to find the overall best TSP tour by using a branch-and-bound based algorithm. This algorithm can be expensive for large-scale problems. If MILP=OFF, then PROC OPTNET uses its initial heuristics to find a feasible, but not necessarily optimal, tour as quickly as possible. Table 2.27 describes the valid values for this option.

Table 2.27: Values for MILP= Option

number	string	Description
1	ON	Uses a mixed-integer linear programming solver
0	OFF	Does not use a mixed-integer linear programming solver

NODESEL=number | string

specifies the branch-and-bound node selection strategy option or its corresponding value number, as listed in Table 2.28.

Table 2.28: Values for NODESEL= Option

number	string	Description
–1	AUTOMATIC	Uses automatic node selection
0	BESTBOUND	Chooses the node with the best relaxed objective (best-bound-first strategy)
1	BESTESTIMATE	Chooses the node with the best estimate of the integer objective value (best-estimate-first strategy)
2	DEPTH	Chooses the most recently created node (depth-first strategy)

The default is AUTOMATIC. For more information about node selection, see Chapter 11: The OPTMILP Procedure in SAS/OR 12.1 User's Guide: Mathematical Programming.

OUT=SAS-data-set

specifies the output data set to contain the solution to the traveling salesman problem.

PROBE=number | string

specifies a probing option or its corresponding value number, as listed in Table 2.29:

Table 2.29: Values for PROBE= Option

number	string	Description
–1	AUTOMATIC	Uses an automatic probing strategy
0	NONE	Disables probing
1	MODERATE	Uses the probing moderately
2	AGGRESSIVE	Uses the probing aggressively

The default value is NONE.

RELOBJGAP=number

specifies a stopping criterion that is based on the best integer objective (BestInteger) and the objective of the best remaining node (BestBound). The relative objective gap is equal to

$\mid \mbox{BestInteger} - \mbox{BestBound}\mid / \left(\mbox{1E$-$10}~ + \mid \mbox{BestBound}\mid \right)$

When this value becomes less than the specified gap size number, the procedure stops. The value of number can be any number between 0 and 1; the default value is 1E–4.

STRONGITER=number

specifies the number of simplex iterations to be performed for each variable in the candidate list when using the strong branching variable selection strategy. The value of number can be any positive number; the default value is automatically calculated by PROC OPTNET.

STRONGLEN=number

specifies the number of candidates to be used when performing the strong branching variable selection strategy. The value of number can be any positive integer up to the largest four-byte signed integer, which is 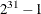$2^{31} - 1$ . The default value is 10.

TARGET=number

specifies a stopping criterion for minimization (maximization) problems. If the best integer objective is better than or equal to number, the procedure stops. The value of number can be any number; the default is the negative (positive) number that has the largest absolute value that can be represented in your operating environment.

VARSEL=number | string

specifies the rule for selecting the branching variable. Table 2.30 lists the valid values for this option.

Table 2.30: Values for VARSEL= Option

number	string	Description
–1	AUTOMATIC	Uses automatic branching variable selection
0	MAXINFEAS	Chooses the variable with maximum infeasibility
1	MININFEAS	Chooses the variable with minimum infeasibility
2	PSEUDO	Chooses a branching variable based on pseudocost
3	STRONG	Uses strong branching variable selection strategy

The default is STRONG. For more information about variable selection, see Chapter 11: The OPTMILP Procedure in SAS/OR 12.1 User's Guide: Mathematical Programming.