The OPTNET Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryPROC OPTNET StatementBICONCOMP StatementCLIQUE StatementCONCOMP StatementCYCLE StatementDATA_ADJ_MATRIX_VAR StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementSHORTPATH StatementTRANSITIVE_CLOSURE StatementTSP Statement
Functional SummaryPROC OPTNET StatementBICONCOMP StatementCLIQUE StatementCONCOMP StatementCYCLE StatementDATA_ADJ_MATRIX_VAR StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementSHORTPATH StatementTRANSITIVE_CLOSURE StatementTSP Statement -
Details

-
Examples
 Articulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities
Articulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities - References
Transitive Closure
The transitive closure of a graph ![]() is a graph
is a graph ![]() such that for all
such that for all ![]() there is a link
there is a link ![]() if and only if there exists a path from
if and only if there exists a path from ![]() to
to ![]() in
in ![]() .
.
The transitive closure of a graph can help to efficiently answer questions about reachability. Suppose you want to answer
the question of whether you can get from node ![]() to node
to node ![]() in the original graph
in the original graph ![]() . Given the transitive closure
. Given the transitive closure ![]() of
of ![]() , you can simply check for the existence of link
, you can simply check for the existence of link ![]() to answer the question. This has many applications, including speeding up the processing of structured query languages, which
are often used in databases.
to answer the question. This has many applications, including speeding up the processing of structured query languages, which
are often used in databases.
In PROC OPTNET, the transitive closure algorithm can be invoked by using the TRANSITIVE_CLOSURE statement. The options for this statement are described in the section TRANSITIVE_CLOSURE Statement.
The results for the transitive closure algorithm are written to the output data set that is specified in the OUT= option in
the TRANSITIVE_CLOSURE statement. The links that define the transitive closure are listed in the output data set with variable
names from and to.
The transitive closure algorithm reports status information in a macro variable called _OROPTNET_TRANSCL_. See the section Macro Variable _OROPTNET_TRANSCL_ for more information about this macro variable.
The algorithm used by PROC OPTNET to compute transitive closure is a sparse version of the Floyd-Warshall algorithm (Cormen,
Leiserson, and Rivest 1990). This algorithm runs in time ![]() and therefore might not scale to very large graphs.
and therefore might not scale to very large graphs.
Transitive Closure of a Simple Directed Graph
This example illustrates the use of the transitive closure algorithm on the simple directed graph ![]() shown in Figure 2.56.
shown in Figure 2.56.
Figure 2.56: A Simple Directed Graph ![]()
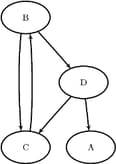
The directed graph ![]() can be represented by the links data set
can be represented by the links data set LinkSetIn as follows:
data LinkSetIn; input from $ to $ @@; datalines; B C B D C B D A D C ;
The following statements calculate the transitive closure and output the results in the data set TransClosure:
proc optnet
graph_direction = directed
data_links = LinkSetIn;
transitive_closure
out = TransClosure;
run;
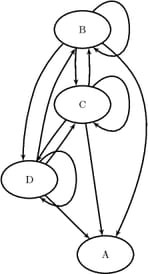
The data set TransClosure contains the transitive closure of ![]() and is shown in Figure 2.57.
and is shown in Figure 2.57.
Figure 2.57: Transitive Closure of a Simple Directed Graph
| Transitive Closure |
| from | to |
|---|---|
| B | C |
| B | D |
| C | B |
| D | A |
| D | C |
| C | C |
| C | D |
| B | B |
| D | B |
| D | D |
| B | A |
| C | A |
The transitive closure of ![]() is shown graphically in Figure 2.58.
is shown graphically in Figure 2.58.
Figure 2.58: Transitive Closure of ![]()
For a more detailed example, see Example 2.6.