The OPTNET Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryPROC OPTNET StatementBICONCOMP StatementCLIQUE StatementCONCOMP StatementCYCLE StatementDATA_ADJ_MATRIX_VAR StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementSHORTPATH StatementTRANSITIVE_CLOSURE StatementTSP Statement
Functional SummaryPROC OPTNET StatementBICONCOMP StatementCLIQUE StatementCONCOMP StatementCYCLE StatementDATA_ADJ_MATRIX_VAR StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementSHORTPATH StatementTRANSITIVE_CLOSURE StatementTSP Statement -
Details

-
Examples
 Articulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities
Articulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities - References
Example 2.2 Cycle Detection for Kidney Donor Exchange
This example looks at an application of cycle detection to help create a kidney donor exchange. Suppose someone needs a kidney
transplant and a family member is willing to donate one. If the donor and recipient are incompatible (because of blood types,
tissue mismatch, and so on), the transplant cannot happen. Now suppose two donor-recipient pairs A and B are in this situation,
but donor A is compatible with recipient B and donor B is compatible with recipient A. Then two transplants can take place
in a two-way swap, shown graphically in Output 2.2.1. More generally, an ![]() -way swap can be performed involving
-way swap can be performed involving ![]() donors and
donors and ![]() recipients (Willingham 2009).
recipients (Willingham 2009).
Output 2.2.1: Kidney Donor Exchange Two-Way Swap
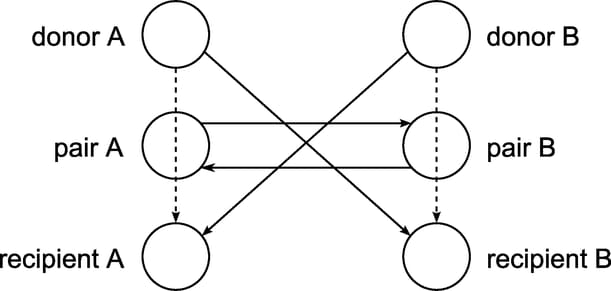
To model this problem, define a directed graph as follows. Each node is an incompatible donor-recipient pair. Link ![]() exists if the donor from node
exists if the donor from node ![]() is compatible with the recipient from node
is compatible with the recipient from node ![]() . The link weight is a measure of the quality of the match. By introducing dummy links with weight 0, you can also include
altruistic donors with no recipients, or recipients without donors. The idea is to find a maximum weight node-disjoint union
of directed cycles. You want the union to be node-disjoint so that no kidney is donated more than once, and you want cycles
so that the donor from node
. The link weight is a measure of the quality of the match. By introducing dummy links with weight 0, you can also include
altruistic donors with no recipients, or recipients without donors. The idea is to find a maximum weight node-disjoint union
of directed cycles. You want the union to be node-disjoint so that no kidney is donated more than once, and you want cycles
so that the donor from node ![]() gives up a kidney if and only if the recipient from node
gives up a kidney if and only if the recipient from node ![]() receives a kidney.
receives a kidney.
Without any other constraints, the problem could be solved as a linear assignment problem, as described in the section Linear Assignment (Matching). But doing so would allow arbitrarily long cycles in the solution. Because of practical considerations (such as travel) and
to mitigate risk, each cycle must have no more than ![]() links. The kidney exchange problem is to find a maximum weight node-disjoint union of short directed cycles.
links. The kidney exchange problem is to find a maximum weight node-disjoint union of short directed cycles.
One way to solve this problem is to explicitly generate all cycles of at most ![]() length and then solve a set packing problem. You can use PROC OPTNET to generate the cycles and then PROC OPTMODEL (see
SAS/OR User's Guide: Mathematical Programming) to read the PROC OPTNET output, formulate the set packing problem, call the mixed integer linear programming solver, and
output the optimal solution.
length and then solve a set packing problem. You can use PROC OPTNET to generate the cycles and then PROC OPTMODEL (see
SAS/OR User's Guide: Mathematical Programming) to read the PROC OPTNET output, formulate the set packing problem, call the mixed integer linear programming solver, and
output the optimal solution.
The following DATA step sets up the problem, first creating a random graph on ![]() nodes with link probability
nodes with link probability ![]() and Uniform(0,1) weight:
and Uniform(0,1) weight:
/* create random graph on n nodes with arc probability p
and uniform(0,1) weight */
%let n = 100;
%let p = 0.02;
data LinkSetIn;
do from = 0 to &n - 1;
do to = 0 to &n - 1;
if from eq to then continue;
else if ranuni(1) < &p then do;
weight = ranuni(2);
output;
end;
end;
end;
run;
The following statements use PROC OPTNET to generate all cycles with length greater than or equal to 2 and less than or equal to 10:
/* generate all cycles with 2 <= length <= max_length */
%let max_length = 10;
proc optnet
loglevel = moderate
graph_direction = directed
data_links = LinkSetIn;
cycle
minLength = 2
maxLength = &max_length
out = Cycles
mode = all_cycles;
run;
%put &_OROPTNET_;
%put &_OROPTNET_CYCLE_;
PROC OPTNET finds 224 cycles of the appropriate length, as shown in Output 2.2.2.
Output 2.2.2: Cycles for Kidney Donor Exchange PROC OPTNET Log
| NOTE: ------------------------------------------------------------------------- |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: Running OPTNET. |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: Reading the links data set. |
| NOTE: There were 194 observations read from the data set WORK.LINKSETIN. |
| NOTE: Data input used 0.00 (cpu: 0.00) seconds. |
| NOTE: Building the input graph storage used 0.00 (cpu: 0.00) seconds. |
| NOTE: The input graph storage is using 0.0 MBs of memory. |
| NOTE: The number of nodes in the input graph is 97. |
| NOTE: The number of links in the input graph is 194. |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: Processing CYCLE statement. |
| NOTE: The graph has 224 cycles. |
| NOTE: Processing cycles used 3.20 (cpu: 3.18) seconds. |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: Creating cycle data set output. |
| NOTE: Data output used 0.00 (cpu: 0.00) seconds. |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: ------------------------------------------------------------------------- |
| NOTE: The data set WORK.CYCLES has 2124 observations and 3 variables. |
| STATUS=OK CYCLE=OK |
| STATUS=OK NUM_CYCLES=224 CPU_TIME=3.18 REAL_TIME=3.20 |
From the resulting data set Cycles, use the following DATA step to convert the cycles into one observation per arc:
/* convert Cycles into one observation per arc */ data Cycles0(keep=c i j); set Cycles; retain last; c = cycle; i = last; j = node; last = j; if order ne 1 then output; run;
Given the set of cycles, you can now formulate a mixed integer linear program (MILP) to maximize the total cycle weight. Let
![]() define the set of cycles of appropriate length,
define the set of cycles of appropriate length, ![]() define the set of nodes in cycle
define the set of nodes in cycle ![]() ,
, ![]() define the set of links in cycle
define the set of links in cycle ![]() , and
, and ![]() denote the link weight for link
denote the link weight for link ![]() . Define a binary decision variable
. Define a binary decision variable ![]() . Set
. Set ![]() to 1 if cycle
to 1 if cycle ![]() is used in the solution; otherwise, set it to 0. Then, the following MILP defines the problem that you want to solve to maximize
the quality of the kidney exchange:
is used in the solution; otherwise, set it to 0. Then, the following MILP defines the problem that you want to solve to maximize
the quality of the kidney exchange:
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The constraint (incomp_pair) ensures that each node (incompatible pair) in the graph is intersected at most once. That is, a donor can donate a kidney only once. You can use PROC OPTMODEL to solve this mixed integer linear programming problem as follows:
/* solve set packing problem to find maximum weight node-disjoint union
of short directed cycles */
proc optmodel;
/* declare index sets and parameters, and read data */
set <num,num> ARCS;
num weight {ARCS};
read data LinkSetIn into ARCS=[from to] weight;
set <num,num,num> TRIPLES;
read data Cycles0 into TRIPLES=[c i j];
set CYCLES = setof {<c,i,j> in TRIPLES} c;
set ARCS_c {c in CYCLES} = setof {<(c),i,j> in TRIPLES} <i,j>;
set NODES_c {c in CYCLES} = union {<i,j> in ARCS_c[c]} {i,j};
set NODES = union {c in CYCLES} NODES_c[c];
num cycle_weight {c in CYCLES} = sum {<i,j> in ARCS_c[c]} weight[i,j];
/* UseCycle[c] = 1 if cycle c is used, 0 otherwise */
var UseCycle {CYCLES} binary;
/* declare objective */
max TotalWeight
= sum {c in CYCLES} cycle_weight[c] * UseCycle[c];
/* each node appears in at most one cycle */
con node_packing {i in NODES}:
sum {c in CYCLES: i in NODES_c[c]} UseCycle[c] <= 1;
/* call solver */
solve with milp;
/* output optimal solution */
create data Solution from
[c]={c in CYCLES: UseCycle[c].sol > 0.5} cycle_weight;
quit;
%put &_OROPTMODEL_;
PROC OPTMODEL solves the problem by using the mixed integer linear programming solver. As shown in Output 2.2.3, it was able to find a total weight (quality level) of 26.02.
Output 2.2.3: Cycles for Kidney Donor Exchange PROC OPTMODEL Log
| NOTE: There were 194 observations read from the data set WORK.LINKSETIN. |
| NOTE: There were 1900 observations read from the data set WORK.CYCLES0. |
| NOTE: Problem generation will use 2 threads. |
| NOTE: The problem has 224 variables (0 free, 0 fixed). |
| NOTE: The problem has 224 binary and 0 integer variables. |
| NOTE: The problem has 63 linear constraints (63 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The problem has 1900 linear constraint coefficients. |
| NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The MILP presolver value AUTOMATIC is applied. |
| NOTE: The MILP presolver removed 0 variables and 35 constraints. |
| NOTE: The MILP presolver removed 518 constraint coefficients. |
| NOTE: The MILP presolver modified 116 constraint coefficients. |
| NOTE: The presolved problem has 224 variables, 28 constraints, and 1382 |
| constraint coefficients. |
| NOTE: The MILP solver is called. |
| Node Active Sols BestInteger BestBound Gap Time |
| 0 1 4 22.7780692 1080.2049611 97.89% 0 |
| 0 1 4 22.7780692 26.5638757 14.25% 0 |
| 0 1 6 26.0202871 26.0202871 0.00% 0 |
| 0 0 6 26.0202871 26.0202871 0.00% 0 |
| NOTE: The MILP solver added 17 cuts with 1970 cut coefficients at the root. |
| NOTE: Optimal. |
| NOTE: Objective = 26.0202871. |
| NOTE: The data set WORK.SOLUTION has 6 observations and 2 variables. |
| STATUS=OK ALGORITHM=BAC SOLUTION_STATUS=OPTIMAL OBJECTIVE=26.020287143 |
| RELATIVE_GAP=0 ABSOLUTE_GAP=0 PRIMAL_INFEASIBILITY=1.1040848E-8 |
| BOUND_INFEASIBILITY=7.3628972E-9 INTEGER_INFEASIBILITY=7.3628972E-9 |
| BEST_BOUND=26.020287143 NODES=1 ITERATIONS=83 PRESOLVE_TIME=0.03 |
| SOLUTION_TIME=0.11 |
The data set Solution, shown in Output 2.2.4, now contains the cycles that define the best exchange and their associated weight (quality).
Output 2.2.4: Maximum Quality Solution for Kidney Donor Exchange
| c | cycle_weight |
|---|---|
| 12 | 5.84985 |
| 43 | 3.90015 |
| 71 | 5.44467 |
| 124 | 7.42574 |
| 222 | 2.28231 |
| 224 | 1.11757 |