The OPTNET Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryPROC OPTNET StatementBICONCOMP StatementCLIQUE StatementCONCOMP StatementCYCLE StatementDATA_ADJ_MATRIX_VAR StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementSHORTPATH StatementTRANSITIVE_CLOSURE StatementTSP Statement
Functional SummaryPROC OPTNET StatementBICONCOMP StatementCLIQUE StatementCONCOMP StatementCYCLE StatementDATA_ADJ_MATRIX_VAR StatementDATA_LINKS_VAR StatementDATA_MATRIX_VAR StatementDATA_NODES_VAR StatementLINEAR_ASSIGNMENT StatementMINCOSTFLOW StatementMINCUT StatementMINSPANTREE StatementSHORTPATH StatementTRANSITIVE_CLOSURE StatementTSP Statement -
Details

-
Examples
 Articulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities
Articulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities - References
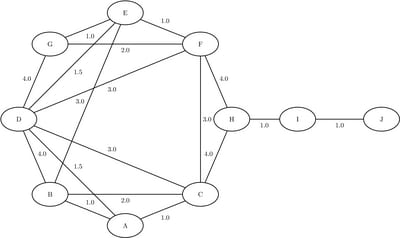
Example 2.5 Minimum Spanning Tree for Computer Network Topology
Consider the problem of designing a small network of computers. In designing the network, the goal is to make sure that each machine in the office can reach every other machine. To accomplish this goal, Ethernet lines must be constructed and run between the machines. The construction costs for each possible link are based approximately on distance and are shown in Output 2.5.1. Besides distance, the costs also reflect some restrictions due to physical boundaries. To connect all the machines in the office at minimal cost, you need to find a minimum spanning tree on the network of possible links.
Output 2.5.1: Potential Office Computer Network
Define the link data set as follows:
data LinkSetInCompNet; input from $ to $ weight @@; datalines; A B 1.0 A C 1.0 A D 1.5 B C 2.0 B D 4.0 B E 3.0 C D 3.0 C F 3.0 C H 4.0 D E 1.5 D F 3.0 D G 4.0 E F 1.0 E G 1.0 F G 2.0 F H 4.0 H I 1.0 I J 1.0 ;
The following statements find a minimum spanning tree:
proc optnet
data_links = LinkSetInCompNet;
minspantree
out = MinSpanTree;
run;
Output 2.5.3 shows the resulting data set MinSpanTree, which is displayed graphically in Output 2.5.2 with the minimal cost links shown in green.
Output 2.5.2: Minimum Spanning Tree for Office Computer Network
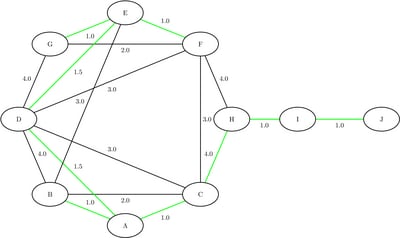
Output 2.5.3: Minimum Spanning Tree of a Computer Network Topology
| from | to | weight |
|---|---|---|
| H | I | 1.0 |
| E | G | 1.0 |
| E | F | 1.0 |
| A | B | 1.0 |
| A | C | 1.0 |
| I | J | 1.0 |
| D | E | 1.5 |
| A | D | 1.5 |
| C | H | 4.0 |
| 13.0 |