The QLIM Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Ordinal Discrete Choice ModelingLimited Dependent Variable ModelsStochastic Frontier Production and Cost ModelsHeteroscedasticity and Box-Cox TransformationBivariate Limited Dependent Variable ModelingSelection ModelsMultivariate Limited Dependent ModelsVariable SelectionTests on ParametersEndogeneity and Instrumental VariablesBayesian AnalysisPrior DistributionsAutomated MCMCOutput to SAS Data SetOUTEST= Data SetNamingODS Table NamesODS Graphics
Ordinal Discrete Choice ModelingLimited Dependent Variable ModelsStochastic Frontier Production and Cost ModelsHeteroscedasticity and Box-Cox TransformationBivariate Limited Dependent Variable ModelingSelection ModelsMultivariate Limited Dependent ModelsVariable SelectionTests on ParametersEndogeneity and Instrumental VariablesBayesian AnalysisPrior DistributionsAutomated MCMCOutput to SAS Data SetOUTEST= Data SetNamingODS Table NamesODS Graphics -
Examples

- References
The multivariate model is similar to bivariate models. The generic form of the multivariate limited dependent variable model is
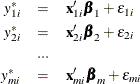
where m is the number of models to be estimated. The vector ![]() has multivariate normal distribution with mean 0 and variance-covariance matrix
has multivariate normal distribution with mean 0 and variance-covariance matrix ![]() . Similar to bivariate models, the likelihood may involve computing multivariate normal integrations. This is done using Monte
Carlo integration. (See Genz (1992); Hajivassiliou and McFadden (1998).)
. Similar to bivariate models, the likelihood may involve computing multivariate normal integrations. This is done using Monte
Carlo integration. (See Genz (1992); Hajivassiliou and McFadden (1998).)
When the number of equations, ![]() , increases in a system, the number of parameters increases at the rate of
, increases in a system, the number of parameters increases at the rate of ![]() because of the correlation matrix. When the number of parameters is large, sometimes the optimization converges but some
of the standard deviations are missing. This usually means that the model is over-parameterized. The default method for computing
the covariance is to use the inverse Hessian matrix. The Hessian is computed by finite differences, and in over-parameterized
cases, the inverse cannot be computed. It is recommended that you reduce the number of parameters in such cases. Sometimes
using the outer product covariance matrix (COVEST=OP option) may also help.
because of the correlation matrix. When the number of parameters is large, sometimes the optimization converges but some
of the standard deviations are missing. This usually means that the model is over-parameterized. The default method for computing
the covariance is to use the inverse Hessian matrix. The Hessian is computed by finite differences, and in over-parameterized
cases, the inverse cannot be computed. It is recommended that you reduce the number of parameters in such cases. Sometimes
using the outer product covariance matrix (COVEST=OP option) may also help.