The QLIM Procedure

Stochastic Frontier Production and Cost Models

Subsections:

Stochastic frontier production models were first developed by Aigner, Lovell, and Schmidt (1977); Meeusen and van den Broeck (1977). Specification of these models allow for random shocks of the production or cost but also include a term for technological or cost inefficiency. Assuming that the production function takes a log-linear Cobb-Douglas form, the stochastic frontier production model can be written as

\[ ln({y_ i}) = \beta _0+\sum _{n} \bbeta _ n\ln (x_{ni})+\epsilon _ i \]

where $\epsilon _ i=v_ i-u_ i$. The $v_ i$ term represents the stochastic error component and $u_ i$ is the nonnegative, technology inefficiency error component. The $v_ i$ error component is assumed to be distributed iid normal and independently from $u_ i$. If $u_ i>0$, the error term, $\epsilon _ i$, is negatively skewed and represents technology inefficiency. If $u_ i<0$, the error term $\epsilon _ i$ is positively skewed and represents cost inefficiency. PROC QLIM models the $u_ i$ error component as a half normal, exponential, or truncated normal distribution.

The Normal-Half Normal Model

In case of the normal-half normal model, $v_ i$ is iid $N(0,\sigma _ v^2)$, $u_ i$ is iid $N^+(0,\sigma _ u^2)$ with $v_ i$ and $u_ i$ independent of each other. Given the independence of error terms, the joint density of v and u can be written as

\[ f(u,v) = \frac{2}{2\pi \sigma _ u\sigma _ v} \exp \left\{ -\frac{u^2}{2\sigma _ u^2} - \frac{v^2}{2\sigma _ v^2} \right\} \]

Substituting $v=\epsilon +u$ into the preceding equation gives

\[ f(u,\epsilon ) = \frac{2}{2\pi \sigma _ u\sigma _ v} \exp \left\{ -\frac{u^2}{2\sigma _ u^2} - \frac{(\epsilon +u)^2}{2\sigma _ v^2} \right\} \]

Integrating u out to obtain the marginal density function of $\epsilon $ results in the following form:

\begin{eqnarray*} f(\epsilon ) & = & \int ^\infty _0 f(u,\epsilon )du \\ & = & \frac{2}{\sqrt {2\pi }\sigma } \left[ 1-\Phi \left( \frac{\epsilon \lambda }{\sigma } \right) \right] \exp \left\{ -\frac{\epsilon ^2}{2\sigma ^2} \right\} \\ & = & \frac{2}{\sigma }\phi \left( \frac{\epsilon }{\sigma } \right) \Phi \left( -\frac{\epsilon \lambda }{\sigma } \right) \end{eqnarray*}

where $\lambda =\sigma _ u/\sigma _ v$ and $\sigma =\sqrt {\sigma _ u^2+\sigma _ v^2}$.

In the case of a stochastic frontier cost model, $v=\epsilon -u$ and

\[ f(\epsilon ) = \frac{2}{\sigma }\phi \left( \frac{\epsilon }{\sigma } \right) \Phi \left( \frac{\epsilon \lambda }{\sigma } \right) \]

The log-likelihood function for the production model with $N$ producers is written as

\[ \ln L = constant - N \ln \sigma +\sum _ i{ \ln \Phi \left( -\frac{\epsilon _ i\lambda }{\sigma } \right) } -\frac{1}{2\sigma ^2}\sum _ i \epsilon ^2_ i \]

The Normal-Exponential Model

Under the normal-exponential model, $v_ i$ is iid $N(0,\sigma _ v^2)$ and $u_ i$ is iid exponential with scale parameter $\sigma _ u$. Given the independence of error term components $u_ i$ and $v_ i$, the joint density of v and u can be written as

\[ f(u,v) = \frac{1}{\sqrt {2\pi }\sigma _ u\sigma _ v} \exp \left\{ -\frac{u}{\sigma _ u} - \frac{v^2}{2\sigma _ v^2} \right\} \]

The marginal density function of $\epsilon $ for the production function is

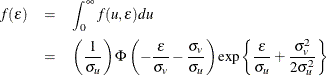
\begin{eqnarray*} f(\epsilon ) & = & \int ^\infty _0 f(u,\epsilon )du \\ & = & \left( \frac{1}{\sigma _ u} \right) \Phi \left( -\frac{\epsilon }{\sigma _ v}-\frac{\sigma _ v}{\sigma _ u} \right) \exp \left\{ \frac{\epsilon }{\sigma _ u}+\frac{\sigma _ v^2}{2\sigma _ u^2} \right\} \end{eqnarray*}

and the marginal density function for the cost function is equal to

\[ f(\epsilon ) = \left( \frac{1}{\sigma _ u} \right) \Phi \left( \frac{\epsilon }{\sigma _ v}-\frac{\sigma _ v}{\sigma _ u} \right) \exp \left\{ -\frac{\epsilon }{\sigma _ u}+\frac{\sigma _ v^2}{2\sigma _ u^2} \right\} \]

The log-likelihood function for the normal-exponential production model with $N$ producers is

\[ \ln L = constant - N \ln \sigma _ u+N\left( \frac{\sigma _ v^2}{2\sigma _ u^2} \right) +\sum _ i\frac{\epsilon _ i}{\sigma _ u} +\sum _ i\ln \Phi \left( -\frac{\epsilon _ i}{\sigma _ v}-\frac{\sigma _ v}{\sigma _ u} \right) \]

The Normal-Truncated Normal Model

The normal-truncated normal model is a generalization of the normal-half normal model by allowing the mean of $u_ i$ to differ from zero. Under the normal-truncated normal model, the error term component $v_ i$ is iid $N(0,\sigma _ v^2)$ and $u_ i$ is iid $N^+(\mu ,\sigma _ u^2)$. The joint density of $v_ i$ and $u_ i$ can be written as

\[ f(u,v) = \frac{1}{ 2\pi \sigma _ u\sigma _ v\Phi \left( \mu /\sigma _ u \right) } \exp \left\{ -\frac{(u-\mu )^2}{2\sigma _ u^2}-\frac{v^2}{2\sigma _ v^2} \right\} \]

The marginal density function of $\epsilon $ for the production function is

\begin{eqnarray*} f(\epsilon ) & = & \int ^\infty _0 f(u,\epsilon )du \\ & = & \frac{1}{ \sqrt {2\pi }\sigma \Phi \left( \mu /\sigma _ u \right) } \Phi \left( \frac{\mu }{\sigma \lambda }-\frac{\epsilon \lambda }{\sigma } \right) \exp \left\{ -\frac{(\epsilon +\mu )^2}{2\sigma ^2} \right\} \\ & = & \frac{1}{\sigma }\phi \left( \frac{\epsilon +\mu }{\sigma } \right) \Phi \left( \frac{\mu }{\sigma \lambda }-\frac{\epsilon \lambda }{\sigma } \right) \left[ \Phi \left( \frac{\mu }{\sigma _ u} \right) \right]^{-1} \end{eqnarray*}

and the marginal density function for the cost function is

\begin{eqnarray*} f(\epsilon ) & = & \frac{1}{\sigma }\phi \left( \frac{\epsilon -\mu }{\sigma } \right) \Phi \left( \frac{\mu }{\sigma \lambda }+\frac{\epsilon \lambda }{\sigma } \right) \left[ \Phi \left( \frac{\mu }{\sigma _ u} \right) \right]^{-1} \end{eqnarray*}

The log-likelihood function for the normal-truncated normal production model with $N$ producers is

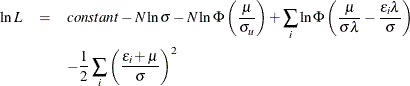
\begin{eqnarray*} \ln L & = & constant - N \ln \sigma -N\ln \Phi \left( \frac{\mu }{\sigma _ u} \right) +\sum _ i\ln \Phi \left( \frac{\mu }{\sigma \lambda }-\frac{\epsilon _ i\lambda }{\sigma } \right) \\ & & -\frac{1}{2}\sum _ i{ \left( \frac{\epsilon _ i+\mu }{\sigma } \right)^2 } \end{eqnarray*}

For more detail on normal-half normal, normal-exponential, and normal-truncated models, see Kumbhakar and Lovell (2000); Coelli, Prasada Rao, and Battese (1998).