The QLIM Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Ordinal Discrete Choice ModelingLimited Dependent Variable ModelsStochastic Frontier Production and Cost ModelsHeteroscedasticity and Box-Cox TransformationBivariate Limited Dependent Variable ModelingSelection ModelsMultivariate Limited Dependent ModelsVariable SelectionTests on ParametersEndogeneity and Instrumental VariablesBayesian AnalysisPrior DistributionsAutomated MCMCOutput to SAS Data SetOUTEST= Data SetNamingODS Table NamesODS Graphics
Ordinal Discrete Choice ModelingLimited Dependent Variable ModelsStochastic Frontier Production and Cost ModelsHeteroscedasticity and Box-Cox TransformationBivariate Limited Dependent Variable ModelingSelection ModelsMultivariate Limited Dependent ModelsVariable SelectionTests on ParametersEndogeneity and Instrumental VariablesBayesian AnalysisPrior DistributionsAutomated MCMCOutput to SAS Data SetOUTEST= Data SetNamingODS Table NamesODS Graphics -
Examples

- References
In sample selection models, one or several dependent variables are observed when another variable takes certain values. For example, the standard Heckman selection model can be defined as
where ![]() and
and ![]() are jointly normal with 0 mean, standard deviations of 1 and
are jointly normal with 0 mean, standard deviations of 1 and ![]() , respectively, and correlation of
, respectively, and correlation of ![]() . Selection is based on the variable z, and y is observed when z has a value of 1. Least squares regression that uses the observed data of y produces inconsistent estimates of
. Selection is based on the variable z, and y is observed when z has a value of 1. Least squares regression that uses the observed data of y produces inconsistent estimates of ![]() . The maximum likelihood method is used to estimate selection models. It is also possible to estimate these models by using
Heckman’s method, which is more computationally efficient. But it can be shown that the resulting estimates, although consistent,
are not asymptotically efficient under a normality assumption. Moreover, this method often violates the constraint on the
correlation coefficient
. The maximum likelihood method is used to estimate selection models. It is also possible to estimate these models by using
Heckman’s method, which is more computationally efficient. But it can be shown that the resulting estimates, although consistent,
are not asymptotically efficient under a normality assumption. Moreover, this method often violates the constraint on the
correlation coefficient ![]() .
.
The log-likelihood function of the Heckman selection model is written as
![\begin{eqnarray*} \ell & =& \sum _{i\in \{ z_{i}=0\} }\ln [1-\Phi (\mb{w}_{i}’\bgamma )] \\ & +& \sum _{i\in \{ z_{i}=1\} } \left\{ \ln \phi (\frac{y_ i-\mb{x_ i}'\bbeta }{\sigma }) - \ln \sigma + \ln \Phi \left(\frac{\mb{w}_{i}'\bgamma + \rho \frac{y_ i-\mb{x_ i}'\bbeta }{\sigma }}{\sqrt {1-\rho ^2}}\right) \right\} \end{eqnarray*}](images/etsug_qlim0233.png)
The selection can be based on only one variable, but the selection can lead to several variables. For example, selection is based on the variable z in the following switching regression model:
If ![]() , then
, then ![]() is observed. If
is observed. If ![]() , then
, then ![]() is observed. Because
is observed. Because ![]() and
and ![]() are never observed at the same time, the correlation between
are never observed at the same time, the correlation between ![]() and
and ![]() cannot be estimated. Only the correlation between z and
cannot be estimated. Only the correlation between z and ![]() and the correlation between z and
and the correlation between z and ![]() can be estimated. This estimation uses the maximum likelihood method.
can be estimated. This estimation uses the maximum likelihood method.
A brief example of the SAS statements for this model can be found in Sample Selection Model.
The Heckman selection model can include censoring or truncation. For a brief example of the SAS statements for these models
see Sample Selection Model with Truncation and Censoring. The following example shows a variable ![]() that is censored from below at zero:
that is censored from below at zero:
In this case, the log-likelihood function of the Heckman selection model needs to be modified as follows to include the censored region:
![\begin{eqnarray*} \ell & =& \sum _{\{ i|z_{i}=0\} }\ln [1-\Phi (\mb{w}_{i}’\bgamma )] \\ & +& \sum _{ \{ i|z_{i}=1,y_{i}=y_{i}^{*}\} } \left\{ \ln \left[\phi (\frac{y_ i-\mb{x_ i}'\bbeta }{\sigma })\right] - \ln \sigma + \ln \left[\Phi \left(\frac{\mb{w}_{i}'\bgamma + \rho \frac{y_ i-\mb{x_ i}'\bbeta }{\sigma }}{\sqrt {1-\rho ^2}}\right)\right] \right\} \\ & +& \sum _{ \{ i|z_{i}=1,y_{i}=0\} } \ln \int _{-\infty } ^{\frac{-\mb{x_ i}'\bbeta }{\sigma }} \int _{-\mb{w_ i}'\gamma } ^{\infty } \phi _2(u,v,\rho ) \, du\, dv \end{eqnarray*}](images/etsug_qlim0240.png)
In case ![]() is truncated from below at 0 instead of censored, the likelihood function can be written as
is truncated from below at 0 instead of censored, the likelihood function can be written as
![\begin{eqnarray*} \ell & =& \sum _{\{ i|z_{i}=0\} }\ln [1-\Phi (\mb{w}_{i}’\bgamma )] \\ & +& \sum _{\{ i|z_{i}=1\} } \left\{ \ln \left[\phi (\frac{y_ i-\mb{x_ i}'\bbeta }{\sigma })\right] - \ln \sigma + \ln \left[\Phi \left(\frac{\mb{w}_{i}'\bgamma + \rho \frac{y_ i-\mb{x_ i}'\bbeta }{\sigma }}{\sqrt {1-\rho ^2}}\right)\right] -\ln \left[\Phi (\mb{x}_{i}’\bbeta /\sigma )\right] \right\} \end{eqnarray*}](images/etsug_qlim0241.png)
Sample selection bias arises from nonrandom selection of the sample from the population. A classic example is using a sample of market wages for working women to estimate female labor supply function. This sample is nonrandom because it includes only the wages of women whose market wage exceeds their home wage at zero hours of work.
A simple selection model can be written as the latent model
where ![]() and
and ![]() are jointly normal with 0 mean, standard deviations of 1 and
are jointly normal with 0 mean, standard deviations of 1 and ![]() , respectively, and correlation of
, respectively, and correlation of ![]() . The dependent variable
. The dependent variable ![]() (wage) is observed if the latent variable
(wage) is observed if the latent variable ![]() (the difference between market wage and reservation wage) is positive or if the indicator variable
(the difference between market wage and reservation wage) is positive or if the indicator variable ![]() (labor force participation) is 1.
(labor force participation) is 1.
The model of interest that applies to the observations in the selected sample can be written as
where ![]() . Hence, the following regression equation is valid for the observations for which
. Hence, the following regression equation is valid for the observations for which ![]() :
:
Therefore, estimates of ![]() that are obtained from the OLS regression of y on
that are obtained from the OLS regression of y on ![]() by using the selected sample (that is, the sample for which
by using the selected sample (that is, the sample for which ![]() ) suffer from omitted variable bias if selection bias is really the case. Although maximum likelihood estimation of
) suffer from omitted variable bias if selection bias is really the case. Although maximum likelihood estimation of ![]() is consistent and efficient, Heckman’s two-step method is more frequently used. Heckman’s two-step method can be requested
by specifying the HECKIT option of the QLIM statement.
is consistent and efficient, Heckman’s two-step method is more frequently used. Heckman’s two-step method can be requested
by specifying the HECKIT option of the QLIM statement.
Heckman’s two-step method is as follows:
-
Obtain
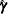 , the estimate of the parameters of the probability that
, the estimate of the parameters of the probability that 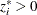 , by using regressors
, by using regressors 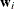 and the binary dependent variable
and the binary dependent variable  by probit analysis for the full sample. Compute
by probit analysis for the full sample. Compute 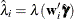 .
.
-
Obtain
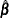 and
and 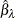 , the estimates of
, the estimates of 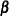 and
and 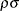 , by least squares regression of
, by least squares regression of 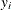 on
on 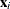 and
and 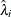 by using observations on the selected subsample.
by using observations on the selected subsample.
The standard least squares estimators of the population variance ![]() and the variances of the estimated coefficients are incorrect. To test hypotheses, the correct ones need to be calculated.
An estimator of
and the variances of the estimated coefficients are incorrect. To test hypotheses, the correct ones need to be calculated.
An estimator of ![]() is
is
where ![]() is the selected subsample size,
is the selected subsample size, ![]() is the residual for the ith observation obtained from step 2, and
is the residual for the ith observation obtained from step 2, and ![]() . Let
. Let ![]() be an
be an ![]() matrix with ith row
matrix with ith row ![]() , and define
, and define ![]() similarly with ith row
similarly with ith row ![]() . Then the estimator of the asymptotic covariance of
. Then the estimator of the asymptotic covariance of ![]() is
is
where ![]() ,
, ![]() , and
, and
where ![]() is the estimator of the asymptotic covariance of the probit coefficients that are obtained in step 1. When you specify the
HECKIT option, PROC QLIM uses a numerical estimated asymptotic variance.
is the estimator of the asymptotic covariance of the probit coefficients that are obtained in step 1. When you specify the
HECKIT option, PROC QLIM uses a numerical estimated asymptotic variance.
When the HECKIT option is specified, PROC QLIM reports the corrected standard errors for ![]() automatically. However, if you need the conventional OLS standard errors, you can specify the HECKIT(UNCORRECTED) option.
automatically. However, if you need the conventional OLS standard errors, you can specify the HECKIT(UNCORRECTED) option.
In the selected regression model, when the coefficient of ![]() is 0, you do not need Heckman’s two-step estimation method; a simple regression of y on
is 0, you do not need Heckman’s two-step estimation method; a simple regression of y on ![]() produces consistent estimates for
produces consistent estimates for ![]() , and the OLS standard errors are correct. Thus, a standard t test on
, and the OLS standard errors are correct. Thus, a standard t test on ![]() (which uses the estimate from step 2 and the uncorrected standard errors) is a valid test of the null hypothesis of no selection
bias.
(which uses the estimate from step 2 and the uncorrected standard errors) is a valid test of the null hypothesis of no selection
bias.
Although Heckman’s two-step method uses the OLS method in the second stage, you can request the ML method by specifying the
HECKIT(SECONDSTAGE=ML) option. When the second-stage method is the ML method, the model for ![]() can be nonlinear.
can be nonlinear.