The PANEL Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Specifying the Input DataSpecifying the Regression ModelUnbalanced DataMissing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsFirst-Differenced Methods for One-Way and Two-Way ModelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR-SquareSpecification TestsPanel Data Poolability TestPanel Data Cross-Sectional Dependence TestPanel Data Unit Root TestsLagrange Multiplier (LM) Tests for Cross-Sectional and Time EffectsTests for Serial Correlation and Cross-Sectional EffectsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names
Specifying the Input DataSpecifying the Regression ModelUnbalanced DataMissing ValuesComputational ResourcesRestricted EstimatesNotationOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsFirst-Differenced Methods for One-Way and Two-Way ModelsBetween EstimatorsPooled EstimatorOne-Way Random-Effects ModelTwo-Way Random-Effects ModelParks Method (Autoregressive Model)Da Silva Method (Variance-Component Moving Average Model)Dynamic Panel EstimatorLinear Hypothesis TestingHeteroscedasticity-Corrected Covariance MatricesHeteroscedasticity- and Autocorrelation-Consistent Covariance MatricesR-SquareSpecification TestsPanel Data Poolability TestPanel Data Cross-Sectional Dependence TestPanel Data Unit Root TestsLagrange Multiplier (LM) Tests for Cross-Sectional and Time EffectsTests for Serial Correlation and Cross-Sectional EffectsTroubleshootingCreating ODS GraphicsOUTPUT OUT= Data SetOUTEST= Data SetOUTTRANS= Data SetPrinted OutputODS Table Names -
Example

- References
Breusch and Pagan (1980) propose a Lagrange multiplier (LM) statistic to test the null hypothesis of zero cross-sectional error correlations. Let
![]() be the OLS estimate of the error term
be the OLS estimate of the error term ![]() under the null hypothesis. Then the pairwise cross-sectional correlations can be estimated by the sample counterparts
under the null hypothesis. Then the pairwise cross-sectional correlations can be estimated by the sample counterparts ![]() ,
,
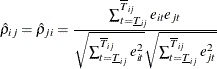
where ![]() and
and ![]() are the lower bound and upper bound, respectively, which mark the overlap time periods for the cross sections i and j. If the panel is balanced,
are the lower bound and upper bound, respectively, which mark the overlap time periods for the cross sections i and j. If the panel is balanced, ![]() and
and ![]() . Let
. Let ![]() denote the number of overlapped time periods (
denote the number of overlapped time periods (![]() ). Then the Breusch-Pagan LM test statistic can be constructed as
). Then the Breusch-Pagan LM test statistic can be constructed as
When N is fixed and ![]() ,
, ![]() . So the test is not applicable as
. So the test is not applicable as ![]() .
.
Because ![]() , are asymptotically independent under the null hypothesis of zero cross-sectional correlation,
, are asymptotically independent under the null hypothesis of zero cross-sectional correlation, ![]() . Then the following modified Breusch-Pagan LM statistic can be considered to test for cross-sectional dependence:
. Then the following modified Breusch-Pagan LM statistic can be considered to test for cross-sectional dependence:
Under the null hypothesis, ![]() as
as ![]() , and then
, and then ![]() . But because
. But because ![]() is not correctly centered at zero for finite
is not correctly centered at zero for finite ![]() , the test is likely to exhibit substantial size distortion for large N and small
, the test is likely to exhibit substantial size distortion for large N and small ![]() .
.
Pesaran (2004) proposes a cross-sectional dependence test that is also based on the pairwise correlation coefficients ![]() ,
,
The test statistic has a zero mean for fixed N and ![]() under a wide class of panel data models, including stationary or unit root heterogeneous dynamic models that are subject
to multiple breaks. For each
under a wide class of panel data models, including stationary or unit root heterogeneous dynamic models that are subject
to multiple breaks. For each ![]() , as
, as ![]() ,
, ![]() . Therefore, for N and
. Therefore, for N and ![]() tending to infinity in any order,
tending to infinity in any order, ![]() .
.
To enhance the power against the alternative hypothesis of local dependence, Pesaran (2004) proposes the CDp test. Local dependence is defined with respect to a weight matrix, ![]() . Therefore, the test can be applied only if the cross-sectional units can be given an ordering that remains immutable over
time. Under the alternative hypothesis of a pth-order local dependence, the CD statistic can be generalized to a local CD test, CDp,
. Therefore, the test can be applied only if the cross-sectional units can be given an ordering that remains immutable over
time. Under the alternative hypothesis of a pth-order local dependence, the CD statistic can be generalized to a local CD test, CDp,
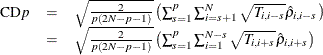
where ![]() . When
. When ![]() , CDp reduces to the original CD test. Under the null hypothesis of zero cross-sectional dependence, the CDp statistic is centered at zero for fixed N and
, CDp reduces to the original CD test. Under the null hypothesis of zero cross-sectional dependence, the CDp statistic is centered at zero for fixed N and ![]() , and CD
, and CD![]() as
as ![]() and
and ![]() .
.