The PANEL Procedure

Dynamic Panel Estimator

Subsections:

For an example on dynamic panel estimation using GMM option, see The Cigarette Sales Data: Dynamic Panel Estimation with GMM.

Consider the case of the following general model:

\[ \mi{y} _\mi {it} = \Sigma _\mi {l = 1} ^\mi {maxlag} \phi _\mi {l} \mi{y} _\mi {i(t-l)} + \Sigma _\mi {k = 1} ^\mi {K} \beta _\mi {k} \mi{x} _\mi {itk} + \gamma _\mi {i} + \alpha _\mi {t} + \epsilon _\mi {it} \]

The x variables can include ones that are correlated or uncorrelated to the individual effects, predetermined, or strictly exogenous. The variable $x_{it}^{p}$ is defined as predetermined in the sense that $E\left(x_{it}^{p}\epsilon _\mi {is}\right)\neq 0$ for $s<t$ and zero otherwise. The variable $x_{it}^{e}$ is defined as strictly exogenous if $E\left(x_{it}^{e}\epsilon _\mi {is}\right)=0$ for all s and t. The $\gamma _{i}$ and $\alpha _{t}$ are cross-sectional and time series fixed effects, respectively. Arellano and Bond (1991) show that it is possible to define conditions that should result in a consistent estimator.

Consider the simple case of an autoregression in a panel setting (with only individual effects):

\[ \mi{y} _\mi {it} = \phi \mi{y} _\mi {i(t-1)} + \gamma _\mi {i} + \epsilon _\mi {it} \]

Differencing the preceding relationship results in:

\[ \Delta \mi{y} _\mi {it} = \phi \Delta \mi{y} _\mi {i(t-1)} + \nu _\mi {it} \]

where $\nu _\mi {it} = \epsilon _\mi {it}- \epsilon _\mi {it-1} $.

Obviously, $\mi{y}_{it} $ is not exogenous. However, Arellano and Bond (1991) show that it is still useful as an instrument, if properly lagged. This instrument is required with the option DEPVAR(LEVEL).

For $t = 2$ (assuming the first observation corresponds to time period 1) you have,

\[ \Delta \mi{y} _\mi {i2} = \phi \Delta \mi{y} _\mi {i1} + \nu _\mi {i2} \]

Using $\mi{y} _\mi {i1} $ as an instrument is not a good idea since $\mr{Cov}\left(\epsilon _\mi {i1}, \nu _\mi {i2} \right)\neq 0$. Therefore, since it is not possible to form a moment restriction, you discard this observation.

For $t = 3$ you have,

\[ \Delta \mi{y} _\mi {i3} = \phi \Delta \mi{y} _\mi {i2} + \nu _\mi {i3} \]

Clearly, you have every reason to suspect that $\mr{Cov}\left(\epsilon _\mi {i1}, \nu _\mi {i3} \right)=0$. This condition forms one restriction.

For $t = 4$, both $\mr{Cov}\left(\epsilon _\mi {i1}, \nu _\mi {i4} \right)=0$ and $\mr{Cov}\left(\epsilon _\mi {i2}, \nu _\mi {i4} \right)=0$ must hold.

Proceeding in that fashion, you have the following matrix of instruments,

\[ \mb{Z} _\mi {i} = \left( \begin{array}{*{10}{c}} \mi{y} _\mi {i1} & 0 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & \mi{y} _\mi {i1} & \mi{y} _\mi {i2} & 0 & \cdots & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \mi{y} _\mi {i1} & \mi{y} _\mi {i2} & \mi{y} _\mi {i3} & 0 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & & & & \vdots & & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & \mi{y} _\mi {i1} & \cdots & \mi{y} _\mi {i(T-2)} \\ \end{array} \right) \]

Using the instrument matrix, you form the weighting matrix $\mb{A} _\mb {N} $ as

\[ \mb{A} _\mb {N} = \left(\frac{1}{N}\sum _\mi {i} ^{N} \mb{Z} _\mi {i} ^{'} \mb{H} _\mi {i} \mb{Z} _\mi {i} \right)^{-1} \]

The initial weighting matrix is

\[ \mb{H} _\mi {i} = \left( \begin{array}{*{10}{r}} 2 & -1 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 & 0 \\ -1 & 2 & -1 & 0 & \cdots & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 2 & -1 & 0 & \cdots & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & & & & \vdots & & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 2 & -1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 2 \\ \end{array} \right) \]

Note that the maximum size of the $\mb{H} _\mi {i} $ matrix is T–2. The origins of the initial weighting matrix are the expected error covariances. Notice that on the diagonals,

\[ E\left( \nu _\mi {it} \nu _\mi {it} \right) = E\left( \epsilon _\mi {it} ^{2} - 2\epsilon _\mi {it} \epsilon _\mi {i(t-1)} + \epsilon _\mi {i(t-1)} ^{2} \right) = 2\sigma _{\epsilon }^{2} \]

and off diagonals,

\[ E\left( \nu _\mi {it} \nu _\mi {i(t-1)} \right) = E\left( \epsilon _\mi {it} \epsilon _\mi {i(t-1)} - \epsilon _\mi {it} \epsilon _\mi {i(t-2)} - \epsilon _\mi {i(t-1)} \epsilon _\mi {i(t-1)} + \epsilon _\mi {i(t-1)} \epsilon _\mi {i(t-2)} \right) =-\sigma _{\epsilon }^{2} \]

If you let the vector of lagged differences (in the series $\mi{y} _\mi {it} $) be denoted as $\Delta \mi{y} _\mi {i-} $ and the dependent variable as $\Delta \mi{y} _\mi {i}$, then the optimal GMM estimator is

\[ \phi = \left[ \left( \sum _{i} \Delta \mi{y} _\mi {i-} ^{'}\mb{Z} _\mi {i} \right) \mb{A} _\mb {N} \left( \sum _{i} \mb{Z} _\mi {i} ^{'}\Delta \mi{y} _\mi {i-} \right) \right]^{-1} \left( \sum _{i} \Delta \mi{y} _\mi {i-} ^{'}\mb{Z} _\mi {i} \right) \mb{A} _\mb {N} \left( \sum _{i} \mb{Z} _\mi {i} ^{'}\Delta \mi{y} _\mi {i} \right) \]

Using the estimate, ${\hat\phi }$, you can obtain estimates of the errors, ${\hat\epsilon }$, or the differences, ${\hat\nu }$. From the errors, the variance is calculated as,

\[ \sigma ^{2} = \frac{{\hat\epsilon }^{'}{\hat\epsilon }}{M - 1} \]

where ${\mi{M} = {\sum }^{\mi{N} }_{i=1}\mi{T} _{i}}$ is the total number of observations. With differenced equations, since we lose the first two observations, $\mi{M} = {\sum }^{\mi{N} }_{i=1}\left(\mi{T} _{i}-2\right)$.

Furthermore, you can calculate the variance of the parameter as,

\[ \sigma ^{2}\left[ \left( \Sigma _{i} \Delta \mi{y} _\mi {i-} ^{'}\mb{Z} _\mi {i} \right) \mb{A} _\mb {N} \left( \sum _{i} \mb{Z} _\mi {i} ^{'}\Delta \mi{y} _\mi {i-} \right) \right]^{-1} \]

Alternatively, you can view the initial estimate of the $\phi $ as a first step. That is, by using ${\hat\phi }$, you can improve the estimate of the weight matrix, $\mb{A} _\mb {N} $.

Instead of imposing the structure of the weighting, you form the $\mb{H} _\mi {i} $ matrix through the following:

\[ \mb{H} _\mi {i} = {\hat\bnu }_{i}{\hat\bnu }_ i^{'} \]

You then complete the calculation as previously shown. The PROC PANEL option GMM2 specifies this estimation.

The case of multiple right-hand-side variables illustrates more clearly the power of Arellano and Bond (1991); Arellano and Bover (1995).

Considering the general case you have:

\[ \mi{y} _\mi {it} = \sum _\mi {l = 1} ^\mi {maxlag} \phi _\mi {l} \mi{y} _\mi {i(t-l)} + \bbeta \mb{X} _\mi {i} + \gamma _\mi {i} + \alpha _\mi {t} + \epsilon _\mi {it} \]

It is clear that lags of the dependent variable are both not exogenous and correlated to the fixed effects. However, the independent variables can fall into one of several categories. An independent variable can be correlated[2] and exogenous, uncorrelated and exogenous, correlated and predetermined, and uncorrelated and predetermined. The category in which an independent variable is found influences when or whether it becomes a suitable instrument. Note, however, that neither PROC PANEL nor Arellano and Bond require that a regressor be an instrument or that an instrument be a regressor.

First, suppose that the variables are all correlated with the individual effects $\gamma _\mi {i}$. Consider the question of exogenous or predetermined. An exogenous variable is not correlated with the error term $\epsilon _\mi {it}-\epsilon _\mi {i,t-1}$ in the differenced equations. Therefore, all observations (on the exogenous variable) become valid instruments at all time periods. If the model has only one instrument and it happens to be exogenous, then the optimal instrument matrix looks like,

\[ \mb{Z} _\mi {i} = \left( \begin{array}{*{5}{c}} \mi{x} _\mi {i1} \cdots \mi{x} _\mi {iT} & 0 & 0 & 0 & 0 \\ 0 & \mi{x} _\mi {i1} \cdots \mi{x} _\mi {iT} & 0 & 0 & 0 \\ 0 & 0 & \mi{x} _\mi {i1} \cdots \mi{x} _\mi {iT} & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \mi{x} _\mi {i1} \cdots \mi{x} _\mi {iT} \\ \end{array} \right) \]

The situation for the predetermined variables becomes a little more difficult. A predetermined variable is one whose future realizations can be correlated to current shocks in the dependent variable. With such an understanding, it is admissible to allow all current and lagged realizations as instruments. In other words you have,

\[ \mb{Z} _\mi {i} = \left( \begin{array}{*{5}{c}} \mi{x} _\mi {i1} & 0 & 0 & 0 & 0 \\ 0 & \mi{x} _\mi {i1} \mi{x} _\mi {i2} & 0 & 0 & 0 \\ 0 & 0 & \mi{x} _\mi {i1} \cdots \mi{x} _\mi {i3} & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \mi{x} _\mi {i1} \cdots \mi{x} _\mi {i(T-1)} \\ \end{array} \right) \]

When the data contain a mix of endogenous, exogenous, and predetermined variables, the instrument matrix is formed by combining the three. For example, the third observation would have one observation on the dependent variable as an instrument, three observations on the predetermined variables as instruments, and all observations on the exogenous variables.

Now consider some variables, denoted as $x_{1it}$, that are not correlated with the individual effects $\gamma _\mi {i}$. There is yet another set of moment restrictions that can be used. An uncorrelated variable means that the variable’s level is not affected by the individual specific effect. You write the preceding general model as

\[ \mi{y} _\mi {it} = \sum _\mi {l = 1} ^\mi {maxlag} \phi _\mi {l} \mi{y} _\mi {i(t-l)} + \Sigma _\mi {k = 1} ^\mi {K} \beta _\mi {k} \mi{x} _\mi {itk} + \alpha _\mi {t} + \mu _\mi {it} \]

where $\mu _\mi {it} = \gamma _\mi {i} + \epsilon _\mi {it} $.

Because the variables are uncorrelated with $\gamma _{i}$ and thus uncorrelated with the error term $\mu _\mi {it}$ in the level equations, you can use the difference and level equations to perform a system estimation. That is, the uncorrelated variables imply moment restrictions on the level equations. Given the previously used restrictions for the equations in first differences, there are T extra restrictions. For predetermined variables, Arellano and Bond (1991) use the extra restrictions $E\left(\mu _{i2}x_{1i1}^{p}\right)=0$ and $E\left(\mu _{it}x_{1it}^{p}\right)=0$ for $t=2,\ldots ,T$. The instrument matrix becomes

\[ \mb{Z} _\mi {i} ^{*} = \left( \begin{array}{*{9}{c}} \mb{Z} _\mi {i} & 0 & 0 & 0 & \cdots & 0 \\ 0 & x^\mi {p} _\mi {1i1} & x^\mi {p} _\mi {1i2} & 0 & \cdots & 0\\ 0 & 0 & 0& x^\mi {p} _\mi {1i3} & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0& 0& \cdots & x^\mi {p} _\mi {1iT} \\ \end{array} \right) \]

For exogenous variables $x_{1it}^{e}$ Arellano and Bond (1991) use $E\left(T^{-1}\sum _{s=1}^{T}\mu _{is}x_{1it}^{e}\right)=0$. PROC PANEL uses the same ones as the predetermined variables—that is, $E\left(\mu _{i2}x_{1i1}^{e}\right)=0$ and $E\left(\mu _{it}x_{1it}^{e}\right)=0$ for $t=2,\ldots ,T$. If you denote the new instrument matrix by using the full complement of instruments available by an asterisk and if both $x^\mi {p} $ and $x^\mi {e} $ are uncorrelated, then you have

\[ \mb{Z} _\mi {i} ^{*} = \left( \begin{array}{*{9}{c}} \mb{Z} _\mi {i} & 0 & 0 & 0 & 0 & 0 & 0& 0 & 0 \\ 0 & x^\mi {p} _\mi {i1} & x^\mi {e} _\mi {i1} & x^\mi {p} _\mi {i2} & x^\mi {e} _\mi {i2}& 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0& x^\mi {p} _\mi {i3} & x^\mi {e} _\mi {i3}& 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 0 & 0& \cdots & x^\mi {p} _\mi {iT} & x^\mi {e} _\mi {iT} \\ \end{array} \right) \]

When the lagged dependent variable is included as the explanatory variable (as in the dynamic panel data models), Blundell and Bond (1998) suggest the system GMM to use $T-2$ extra-moment restrictions, which use the lagged differences as the instruments for the level:

\[ E\left(\mu _{it}\Delta y_{i,t-1}\right)=0\hspace{0.3 in}\text {for }t=3,\ldots ,T \]

This additional set of moment conditions are required by DEPVAR(DIFF) option. The corresponding instrument matrix is

\[ \mb{Z} _\mi {li} ^{y} = \left( \begin{array}{*{9}{c}} 0 & 0 & 0 & \cdots & 0\\ 0 & \Delta y_{i2} & 0 & \cdots & 0\\ 0 & 0 & \Delta y_{i3} & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & \Delta y_{i(T-1)} \\ \end{array} \right) \]

Blundell and Bond (1998) argue that the system GMM that uses these extra conditions significantly increases the efficiency of the estimator, especially under strong serial correlation in the dependent variables.[3]

Except for those GMM-type instruments, PROC PANEL can also handle standard instruments by using the lists that you specify in the LEVELEQ= and DIFFEQ= options. Denote $l_{it}$ and $d_{it}$ as the standard instruments that are specified for the level equation and differenced equation, respectively. The additional moment restrictions are $E\left(\mu _{it}l_{it}\right)=0$ for $t=1,\ldots ,T$ for level equations and $E\left(\Delta \epsilon _\mi {it}d_{it}\right)=0$ for $t=2,\ldots ,T$ for differenced equations. The instrument matrix for the level and differenced equations are $\mb{Z}_\mi {li}$ and $\mb{Z}_\mi {di}$, respectively, as follows:

\[ \mb{Z} _\mi {li} = \left( \begin{array}{*{5}{c}} \mi{l} _\mi {i1}& 0 & 0 & 0 & 0 \\ 0 & \mi{l} _\mi {i2} & 0 & 0 & 0 \\ 0 & 0 & \mi{l} _\mi {i3} & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \mi{l} _\mi {iT} \\ \end{array} \right) \]
\[ \mb{Z} _\mi {di} = \left( \begin{array}{*{5}{c}} \mi{d} _\mi {i1}& 0 & 0 & 0 & 0 \\ 0 & \mi{d} _\mi {i2} & 0 & 0 & 0 \\ 0 & 0 & \mi{d} _\mi {i3} & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \mi{d} _\mi {iT} \\ \end{array} \right) \]

To put the differenced and level equations together, for the system GMM estimator, the instrument matrix can be constructed as

\[ \mb{Z} _\mi {i} = \left( \begin{array}{*{5}{c}} \mb{Z} _\mi {di}& 0 & 0 & 0 & 0\\ 0 & \mb{Z} _\mi {li}^{e}& \mb{Z} _\mi {li}^{p}& \mb{Z} _\mi {li}& \mb{Z} _\mi {li}^{y}\\ \end{array} \right) \]

where $\mb{Z} _\mi {li}^{e}$ and $\mb{Z} _\mi {li}^{p}$ correspond to the exogenous and predetermined uncorrelated variables, respectively.

The formation of the initial weighting matrix becomes somewhat problematic. If you denote the new weighting matrix with an asterisk, then you can write

\[ \mb{A} _\mb {N} ^{*} = \left(\frac{1}{N}\sum _\mi {i} ^{N} \mb{Z} _\mi {i} ^{* '} \mb{H} _\mi {i} ^{*} \mb{Z} _\mi {i} ^{*} \right)^{-1} \]

where

\[ \mb{H} _\mi {i} ^{*} = \left( \begin{array}{*{5}{c}} \mb{H} _\mi {i} & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ \end{array} \right) \]

To finish, you write out the two equations (or two stages) that are estimated,

\[ \Delta \mi{y} _\mi {it} = {\bbeta }^{*}\Delta \mb{S} _\mi {it} + \alpha _\mi {t}- \alpha _\mi {t-1} + \nu _\mi {it} \\ \mi{y} _\mi {it} = {\bbeta }^{*}\mb{S} _\mi {it} + \gamma _\mi {i} + \alpha _\mi {t} + \epsilon _\mi {it} \]

where $\mb{S} _\mi {it} $ is the matrix of all explanatory variables—lagged endogenous, exogenous, and predetermined.

Let $\mi{\mb{y}} _\mi {it} ^{*}$ be given by

\[ \begin{array}{*{4}{c}} \mi{\mb{y}} _\mi {it} ^{*} = \left( \begin{array}{*{1}{c}} \Delta \mi{y} _\mi {it} \\ \mi{y} _\mi {it} \\ \end{array} \right) & {\bbeta }^{*} = \left( \begin{array}{*{2}{c}} {\bphi } & {\bbeta } \\ \end{array} \right) & \mb{S}_{it}^{*} = \left( \begin{array}{*{1}{c}} \Delta \mb{S} _\mi {it} \\ \mb{S} _\mi {it} \\ \end{array} \right) & \mb{e}_{i} ^{*} = \left( \begin{array}{*{1}{c}} {\bnu } _\mi {i} \\ {\bmu } _\mi {i}={\bepsilon } _\mi {i}+\gamma _{i} \\ \end{array} \right) \\ \end{array} \]

Using the preceding information, you can get the one-step GMM estimator,

\[ \hat{{\bbeta }}_{1}^{*} = \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*} \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i}^{*} \right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*} \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{y} _\mi {i} ^{*} \right) \]

If the GMM2 or ITGMM option is not specified in the MODEL statement, estimation terminates here. If it terminates, you can obtain the following information.

Variance of the error term comes from the second-stage (level) equations—that is,

\[ \sigma ^{2} = \frac{{\hat\bmu }^{'}{\hat\bmu }}{M - p}=\frac{{\left(\mi{y} _\mi {it} - \hat{{\bbeta }}_{1}^{*}\mb{S} _\mi {it}\right)}^{'}{\left(\mi{y} _\mi {it} - \hat{{\bbeta }}_{1}^{*}\mb{S} _\mi {it}\right)}}{M - p} \]

where p is the number of regressors and M is the number of observations as defined before.

The variance covariance matrix can be obtained from

\[ \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*} \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right) \right]^{-1} \sigma ^{2} \]

Alternatively, you can obtain a robust estimate of the variance covariance matrix by specifying the ROBUST option in the MODEL statement. Without further reestimation of the model, the $\mb{H} _{i}^{*}$ matrix is recalculated as

\[ \mb{H} _{i,2}^{*} = \left( \begin{array}{*{2}{c}} {\hat{\bnu }}_{i}{\hat{\bnu }}_{i}^{'} & 0 \\ 0 & {\hat{\bmu }}_{i}{\hat{\bmu }}_{i}^{'} \\ \end{array} \right) \]

And the weighting matrix becomes

\[ \mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right) = \left(\frac{1}{N}\sum _\mi {i} ^{N} \mb{Z} _\mi {i} ^{* '} \mb{H} _\mi {i,2} ^{*} \mb{Z} _\mi {i} ^{*} \right)^{-1} \]

Using the preceding information, you construct the robust covariance matrix from the following.

Let $\mb{G} $ denote a temporary matrix,

\[ \mb{G} = \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*} \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _{ \mi{i}}^{*}\right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right)\mb{A} _\mb {N} ^{*} \]

The robust covariance estimate of ${\hat{\bbeta }}_{1}^{*}$ is

\[ \mb{V} ^{r}\left( {\hat{\bbeta }}_{1}^{*} \right) = \mb{G} \mb{A} _\mb {N} ^{* -1}\left({\hat{\bbeta }}_{1}^{*}\right) \mb{G} ^{'} \]

Alternatively, you can use the new weighting matrix to form an updated estimate of the regression parameters, as requested by the GMM2 option in the MODEL statement. In short,

\[ {\hat{\bbeta }}_{2}^{*} = \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right) \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right) \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{y} _\mi {i} ^{*} \right) \]

The covariance estimate of the two-step ${\hat{\bbeta }}_{2}^{*}$ becomes

\[ V\left({\hat{\bbeta }}_{2}^{*} \right) = \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right) \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right) \right]^{-1} \]

Similarly, you construct the robust covariance matrix from the following.

Let $\mb{G}_{2} $ denote a temporary matrix,

\[ \mb{G}_{2} = \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*} \left({\hat{\bbeta }}_{1}^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _{ \mi{i}}^{*}\right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right)\mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right) \]

The robust covariance estimate of ${\hat{\bbeta }}_{2}^{*}$ is

\[ \mb{V} ^{r}\left( {\hat{\bbeta }}_{2}^{*} \right) = \mb{G}_{2} \mb{A} _\mb {N} ^{* -1}\left({\hat{\bbeta }}_{2}^{*}\right) \mb{G}_{2}^{'} \]

According to Arellano and Bond (1991), Blundell and Bond (1998), and many others, two-step standard errors are unreliable. Therefore, researchers often base inference on two-step parameter estimates and one-step standard errors. Windmeijer (2005) derives a small-sample bias-corrected variance that uses the first-order Taylor series approximation of the two-step GMM estimator ${\hat{\bbeta }}_{2}^{*}$ around the true value ${\bbeta }^{*}$ as a function of the one-step GMM estimator ${\hat{\bbeta }}_{1}^{*}$,

\[ \begin{array}{*{3}{l}} {\hat{\bbeta }}_{2}^{*}-{\bbeta }^{*}& = & \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{e} _\mi {i} ^{*} \right)\\ & =& \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right) \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right) \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{e} _\mi {i} ^{*} \right) \\ & & +D_{{\bbeta }^{*},\mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)}\left({\hat{\bbeta }}_{1}^{*}-{\bbeta }^{*}\right) +O_{p}\left(N^{-1}\right)\\ \end{array} \]

where $D_{{\bbeta }^{*},\mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)}$ is the first derivative of ${\hat{\bbeta }}_{2}^{*}-{\bbeta }^{*}$ with regard to $\bbeta ’$ evaluated at the true value ${\bbeta }^{*}$. The kth column of $D$ is

\[ \begin{array}{*{1}{l}} \{ D_{{\bbeta }^{*},\mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)}\} _{k}=\\ \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)\frac{\partial \mb{A} _\mb {N} ^{* -1}\left(\bbeta \right)}{\partial \beta _{k}}|_{\bbeta ^{*}}\mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right)\\ \times \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right) \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{e} _\mi {i} ^{*} \right) \\ -\left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)\frac{\partial \mb{A} _\mb {N} ^{* -1}\left(\bbeta \right)}{\partial \beta _{k}}|_{\bbeta ^{*}}\mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{e} _\mi {i} ^{*} \right) \end{array} \]

Because ${\bbeta }^{*}$, $\mb{A} _\mb {N} ^{*}\left({\bbeta }^{*}\right)$, and $\frac{\partial \mb{A} _\mb {N} ^{* -1}\left(\bbeta \right)}{\partial \beta _{k}}|_{\bbeta ^{*}}$ are not feasible, you can replace them with their estimators, ${\hat{\bbeta }}_{2}^{*}$, $\mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)$, and $\frac{\partial \mb{A} _\mb {N} ^{* -1}\left(\bbeta \right)}{\partial \beta _{k}}|_{{\hat{\bbeta }}_{1}^{*}}$, respectively. Denote $\mb{\hat{e}} _\mi {i,2} ^{*}$ as the second-stage error term by

\[ \left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{\hat{e}} _\mi {i,2} ^{*} \right)=0 \]

and

\[ \frac{\partial \mb{A} _\mb {N} ^{* -1}\left(\bbeta \right)}{\partial \beta _{k}}|_{\bbeta ^{*}} =-\frac{1}{N}\sum _{i} \mb{Z} _\mi {i} ^{* '}\left( \begin{array}{*{2}{c}} \Delta \mb{S}_\mi {i,k}\bnu _\mi {i} ^{'}+\bnu _\mi {i}\Delta \mb{S} _\mi {i,k} ^{'}& 0 \\ 0 & \mb{S}_\mi {i,k}\bmu _\mi {i} ^{'}+\bmu _\mi {i}\mb{S} _\mi {i,k} ^{'}\\ \end{array} \right)\mb{Z}_\mi {i} ^{*} \]

The first part vanishes and leaves

\[ \begin{array}{*{4}{l}} \{ D_{{\hat{\bbeta }}_{2}^{*},\mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)}\} _{k}& =& \frac{1}{N}\left[ \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{S} _\mi {i} ^{*} \right) \right]^{-1} \left( \sum _{i}\mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)\\ & & \left(\sum _{i} \mb{Z} _\mi {i} ^{* '}\left( \begin{array}{*{2}{c}} \Delta \mb{S}_\mi {i,k}\hat{\bnu }_\mi {i,1} ^{'}+\hat{\bnu }_\mi {i,1}\Delta \mb{S}_\mi {i,k} ^{'}& 0 \\ 0 & \mb{S}_\mi {i,k}\hat{\bmu }_\mi {i,1}^{'}+\hat{\bmu }_\mi {i,1}\mb{S}_\mi {i,k} ^{'}\\ \end{array} \right)\mb{Z} _\mi {i} ^{*}\right)\mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)\left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\mb{\hat{e}} _\mi {i,2} ^{*} \right)\\ \end{array} \]

Plugging these into the Taylor expansion series yields

\[ V^{c}\left({\hat{\bbeta }}_{2}^{*} \right) = V\left({\hat{\bbeta }}_{2}^{*} \right)+D_{{\hat{\bbeta }}_{2}^{*},\mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)}V\left({\hat{\bbeta }}_{2}^{*} \right)\\ +V\left({\hat{\bbeta }}_{2}^{*} \right)D_{{\hat{\bbeta }}_{2}^{*},\mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)}’+D_{{\hat{\bbeta }}_{2}^{*},\mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)}\mb{V} ^{r}\left( {\hat{\bbeta }}_{1}^{*} \right)D_{{\hat{\bbeta }}_{2}^{*},\mb{A} _\mb {N} ^{*}\left({\hat{\bbeta }}_{1}^{*}\right)}’ \]

As a final note, it possible to iterate more than twice by specifying the ITGMM option. At each iteration, the parameter estimates and its varian-covariance matrix (standard or robust) can be constructed as the one-step and/or two-step GMM estimators. Such a multiple iteration should result in a more stable estimate of the covariance estimate. PROC PANEL allows two convergence criteria. Convergence can occur in the parameter estimates or in the weighting matrices. Let $\mb{A} _\mb {N, k+1} ^{*}$ denote the robust covariance matrix from iteration k, which is used as the weighting matrix in iteration $k+1$. Iterate until

\[ \max _{i,j\leq \mr{dim}\left( \mb{A}^{*}_\mb {N, k} \right) } \frac{\left| \mb{A} _\mb {N, k+1} ^{*}(i,j)- \mb{A} _\mb {N, k} ^{*}(i,j) \right|}{ \left| \mb{A} _\mb {N, k} ^{*}(i,j) \right| } \leq \mr{ATOL} \]

or

\[ \max _{i\leq \mr{dim}\left( {\bbeta }_{k}^{*} \right) } \frac{\left| {\bbeta }_{k+1}^{*}(i)- {\bbeta }_{k}^{*}(i) \right|}{\left| {\bbeta }_{k}^{*}(i) \right|} \leq \mr{BTOL} \]

where ATOL is the tolerance for convergence in the weighting matrix and BTOL is the tolerance for convergence in the parameter estimate matrix. The default convergence criteria is BTOL = 1E–8 for PROC PANEL.

Specification Testing For Dynamic Panel

Specification tests under the GMM in PROC PANEL follow Arellano and Bond (1991) very generally. The first test available is a Sargan/Hansen test of over-identification. The test for a one-step estimation is constructed as

\[ \left( \sum _ i \eta ^{'}_ i \mb{Z^{*}_ i} \right) \mb{A} _\mb {N} ^{*} \left( \sum _ i \mb{Z^{* '}_ i} \eta _ i \right) \sigma ^{2} \]

where $\eta _ i$ is the stacked error term (of the differenced equation and level equation).

When the robust weighting matrix is used, the test statistic is computed as

\[ \left( \sum _ i \eta ^{'}_ i \mb{Z^{*}_ i} \right) \mb{A} _\mb {N, 2} ^{*} \left( \sum _ i \mb{Z^{* '}_ i} \eta _ i \right) \]

This definition of the Sargan test is used for all iterated estimations. The Sargan test is distributed as a $\chi ^2$ with degrees of freedom equal to the number of moment conditions minus the number of parameters.

In addition to the Sargan test, PROC PANEL tests for autocorrelation in the residuals. These tests are distributed as standard normal. PROC PANEL tests the hypothesis that the autocorrelation of the $\mi{l}$th lag is significant.

Define ${\bomega }_\mi {l} $ as the lag of the differenced error, with zero padding for the missing values generated. Symbolically,

\[ {\bomega }_\mi {l,i} = \left( \begin{array}{*{1}{c}} 0 \\ \vdots \\ 0 \\ \bnu _{i,2} \\ \vdots \\ \bnu _{i,T - 1 - \mi{l}} \end{array} \right) \]

You define the constant $k_{0}$ as

\[ k_{0}\left(\mi{l} \right) = \sum _ i {\bomega }_\mi {l,i} ^{'} {\bnu }_\mi {i} \]

You next define the constant $k_{1}$ as

\[ k_{1}\left(\mi{l} \right) = \sum _ i {\bomega }_\mi {l,i} ^{'} \mb{H} _{i} {\bomega }_\mi {l,i} \]

Note that the choice of $\mb{H} _{i}$ is dependent on the stage of estimation. If the estimation is first stage, then you would use the matrix with twos along the main diagonal, and minus ones along the primary subdiagonals. In a robust estimation or multi-step estimation, this matrix would be formed from the outer product of the residuals (from the previous step).

Define the constant $k_{2}$ as

\[ k_{2}\left(\mi{l} \right) = -2 \left(\sum _ i {\bomega }_\mi {l,i} ^{'}\Delta \mb{S} _\mi {i} \right)\mb{G} \left( \sum _{i}\Delta \mb{S} _\mi {i} ^{'}\mb{Z} _\mi {i} \right) \mb{A} _\mb {N,k} \left(\sum _ i\mb{Z} _\mi {i} ^{'} \mb{H} _\mi {i} {\bomega }_\mi {l,i} \right) \]

The matrix $\mb{G} $ is defined as

\[ \mb{G} = \left[ \left( \sum _{i}\Delta \mb{S} _\mi {i} ^{* '}\mb{Z} _\mi {i} ^{*} \right) \mb{A} _\mb {N,k} ^{*} \left( \sum _{i} \mb{Z} _\mi {i} ^{* '}\Delta \mb{S} _\mi {i} ^{*} \right) \right]^{-1} \]

The constant $k_{3}$ is defined as

\[ k_{3}\left(\mi{l} \right) = \left(\sum _{i}{\bomega }_\mi {l,i} ^{'}\Delta \mb{S} _\mi {i} \right) V\left({\bbeta }^{*} \right) \left(\sum _{i}\Delta \mb{S} _\mi {i} ^{'}{\bomega }_\mi {l,i} \right) \]

Using the four quantities, the test for autoregressive structure in the differenced residual is

\[ m\left(\mi{l} \right) = \frac{k_{0}\left(\mi{l} \right)}{\sqrt {k_{1}\left(\mi{l} \right)+k_{2}\left(\mi{l} \right)+k_{3}\left(\mi{l} \right)}} \]

The m statistic is distributed as a normal random variable with mean zero and standard deviation of one.

Instrument Choice

Arellano and Bond’s technique is a very useful method for dealing with any autoregressive characteristics in the data. However, there is one caveat to consider. Too many instruments bias the estimator to the within estimate. Furthermore, many instruments make this technique not scalable. The weighting matrix becomes very large, so every operation that involves it becomes more computationally intensive. The PANEL procedure enables you to specify a bandwidth for instrument selection. For example, specifying MAXBAND=10 means that at most there will be ten time observations for each variable that enters as an instrument. The default is to follow the Arellano-Bond methodology.

In specifying a maximum bandwidth, you can also specify the selection of the time observations. There are three possibilities: leading, trailing (default), and centered. The exact consequence of choosing any of those possibilities depends on the variable type (correlated, exogenous, or predetermined) and the time period of the current observation.

If the MAXBAND option is specified, then the following is true under any selection criterion (let t be the time subscript for the current observation). The first observation for the endogenous variable (as instrument) is max$(t - \mr{MAXBAND}, 1)$ and the last instrument is $t - 2$. The first observation for a predetermined variable is max$(t - \mr{MAXBAND}, 1)$ and the last is $t - 1$. The first and last observation for an exogenous variable is given in the following list:

  • Trailing: If 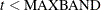$t < \mr{MAXBAND}$, then the first instrument is for the first time period and the last observation is 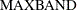$\mr{MAXBAND}$. Otherwise, if 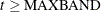$t \geq \mr{MAXBAND}$, then the first observation is 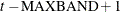$t - \mr{MAXBAND}+1$ and the last instrument to enter is t.

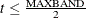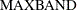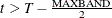  • Centered: If $t \leq \frac{\mr{MAXBAND}}{2}$, then the first observation is the first time period and the last observation is $\mr{MAXBAND}$. If $t > T - \frac{\mr{MAXBAND}}{2}$, then the first instrument included is 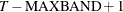$T - \mr{MAXBAND}+1$ and the last observation is T. If 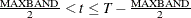$\frac{\mr{MAXBAND}}{2} < t \leq T - \frac{\mr{MAXBAND}}{2}$, then the first included instrument is 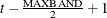$t - \frac{\mr{MAXBAND}}{2}+1$ and the last observation is 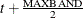$t + \frac{\mr{MAXBAND}}{2}$. If the 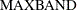$\mr{MAXBAND}$ value is an odd number, the procedure decrements by one.

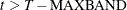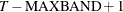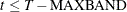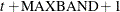  • Leading : If $t > T - \mr{MAXBAND}$, then the first instrument corresponds to time period $T - \mr{MAXBAND}+1$ and the last observation is T. Otherwise, if $t \leq T - \mr{MAXBAND}$, then the first observation is t and the last observation is $t + \mr{MAXBAND}+1$.

The PANEL procedure enables you to include dummy variables to deal with the presence of time effects that are not captured by including the lagged dependent variable. The dummy variables directly affect the level equations. However, this implies that the difference of the dummy variable for time period t and $t-1$ enters the difference equation. The first usable observation occurs at $t=3$. If the level equation is not used in the estimation, then there is no way to identify the dummy variables. Selecting the TIME option gives the same result as that which would be obtained by creating dummy variables in the data set and using those in the regression.

The PANEL procedure gives you several options when it comes to missing values and unbalanced panel. By default, any time period for which there are missing values is skipped. The corresponding rows and columns of $\mb{H} $ matrices are zeroed, and the calculation is continued. Alternatively, you can elect to replace missing values and missing observations with zeros (ZERO), the overall mean of the series (OAM), the cross-sectional mean (CSM), or the time series mean (TSM).


[2] In this section, "correlated" means correlated with the individual effects and "uncorrelated" means uncorrelated with the individual effects.

[3] This happens when $\phi \to 1$ or as $\sigma _{\gamma }^{2}/\sigma _{\epsilon }^{2}\to \infty $. In this case, the lagged dependent variables $y_{i(t-l)}$ become weak instruments for the differenced variables $\Delta y_{it}$.